
International Edition---engineering Mechanics: Statics 4th Edition
4th Edition
ISBN: 9781305856240
Author: Pytel
Publisher: Cengage
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 9, Problem 9.39P
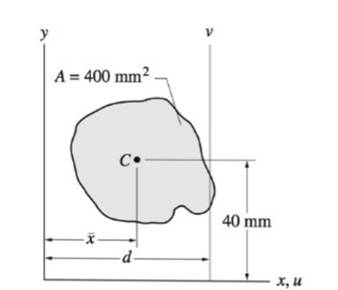
For the region shown,
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
mylabmastering.pearson.com
Chapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY...
P Pearson MyLab and Mastering
Scores
A metal plate of thickness 200 mm with thermal diffusivity 5.6 x10-6 m²/s and thermal
conductivity 20 W/mK is initially at a uniform temperature of 325°C. Suddenly, the 2 sides of
the plate are exposed to a coolant at 15°C for which the convection heat transfer coefficient is
100 W/m²K. Determine temperatures at the surface of the plate after 3 min using
(a) Lumped system analysis
(b) Analytical one term approximation
(c) One dimensional Semi infinite solid
Analyze and discuss the results
Problem 3
This problem maps back to learning
objectives 1-4 & 8.
Consider the particle attached to a spring shown below. The particle
has a mass m and the spring has a spring constant k. The mass-spring
system makes an angle of 0 with respect to the vertical and the
distance between point 0 and the particle can be defined as r. The
spring is unstretched when r = l.
Ꮎ
g
m
a) How many degrees of freedom is this system and what are
they?
b) Derive the equation(s) of motion that govern the movement of
this system.
Chapter 9 Solutions
International Edition---engineering Mechanics: Statics 4th Edition
Ch. 9 - Compute the moment of inertia of the shaded region...Ch. 9 - The properties of the plane region are...Ch. 9 - The moments of inertia of the plane region about...Ch. 9 - The moment of inertia of the plane region about...Ch. 9 - Using integration, find the moment of inertia and...Ch. 9 - Use integration to determine the moment of inertia...Ch. 9 - Determine Ix and Iy for the plane region using...Ch. 9 - Using integration, compute the polar moment of...Ch. 9 - Use integration to compute Ix and Iy for the...Ch. 9 - By integration, determine the moments of inertia...
Ch. 9 - Compute the moment of inertia about the x-axis for...Ch. 9 - By integration, find the moment of inertia about...Ch. 9 - Figure (a) shows the cross section of a column...Ch. 9 - Compute the dimensions of the rectangle shown in...Ch. 9 - Compute Ix and Iy for the W867 shape dimensioned...Ch. 9 - Figure (a) shows the cross-sectional dimensions...Ch. 9 - A W867 section is joined to a C1020 section to...Ch. 9 - Compute Ix and Iy for the region shown.Ch. 9 - Prob. 9.19PCh. 9 - Calculate Ix for the shaded region, knowing that...Ch. 9 - Compute Iy for the region shown, given that...Ch. 9 - Prob. 9.22PCh. 9 - Prob. 9.23PCh. 9 - Determine Ix for the triangular region shown.Ch. 9 - Determine the distance h for which the moment of...Ch. 9 - A circular region of radius R/2 is cut out from...Ch. 9 - Prob. 9.27PCh. 9 - Determine the ratio a/b for which Ix=Iy for the...Ch. 9 - As a round log passes through a sawmill, two slabs...Ch. 9 - Prob. 9.30PCh. 9 - By numerical integration, compute the moments of...Ch. 9 - Use numerical integration to compute the moments...Ch. 9 - The plane region A is submerged in a fluid of...Ch. 9 - Use integration to verify the formula given in...Ch. 9 - For the quarter circle in Table 9.2, verify the...Ch. 9 - Determine the product of inertia with respect to...Ch. 9 - The product of inertia of triangle (a) with...Ch. 9 - Prob. 9.38PCh. 9 - For the region shown, Ixy=320103mm4 and Iuv=0....Ch. 9 - Prob. 9.40PCh. 9 - Calculate the product of inertia with respect to...Ch. 9 - Prob. 9.42PCh. 9 - Prob. 9.43PCh. 9 - The figure shows the cross section of a standard...Ch. 9 - Prob. 9.45PCh. 9 - Prob. 9.46PCh. 9 - Prob. 9.47PCh. 9 - Use numerical integration to compute the product...Ch. 9 - Determine the dimension b of the square cutout so...Ch. 9 - For the rectangular region, determine (a) the...Ch. 9 - Prob. 9.51PCh. 9 - Prob. 9.52PCh. 9 - Prob. 9.53PCh. 9 - Prob. 9.54PCh. 9 - Prob. 9.55PCh. 9 - The u- and v-axes are the principal axes of the...Ch. 9 - The x- and y-axes are the principal axes for the...Ch. 9 - Prob. 9.58PCh. 9 - The inertial properties of the region shown with...Ch. 9 - Determine Iu for the inverted T-section shown....Ch. 9 - Using Ix and Iu from Table 9.2, determine the...Ch. 9 - Show that every axis passing through the centroid...Ch. 9 - Prob. 9.63PCh. 9 - The L806010-mm structural angle has the following...Ch. 9 - Compute the principal centroidal moments of...Ch. 9 - Prob. 9.66PCh. 9 - Determine the principal axes and the principal...Ch. 9 - Compute the principal centroidal moments of...Ch. 9 - Find the moments and the product of inertia of the...Ch. 9 - Determine the moments and product of inertia of...Ch. 9 - Find the principal moments of inertia and the...Ch. 9 - Determine the moments and product of inertia of...Ch. 9 - Prob. 9.73PCh. 9 - Prob. 9.74PCh. 9 - The u- and v-axes are the principal axes of the...Ch. 9 - The x- and y-axes are the principal axes for the...Ch. 9 - Prob. 9.77PCh. 9 - The L806010-mm structural angle has the following...Ch. 9 - Prob. 9.79RPCh. 9 - Prob. 9.80RPCh. 9 - By integration, show that the product of inertia...Ch. 9 - Compute Ix and Iy for the shaded region.Ch. 9 - Using integration, evaluate the moments of inertia...Ch. 9 - The inertial properties at point 0 for a plane...Ch. 9 - Compute Ix and Iy for the shaded region.Ch. 9 - The flanged bolt coupling is fabricated by...Ch. 9 - Prob. 9.87RPCh. 9 - Compute Ix,Iy, and Ixy for the shaded region.Ch. 9 - Determine Ix and Ixy for the shaded region shown.Ch. 9 - Calculate Ix,Iy, and Ixy for the shaded region...Ch. 9 - For the shaded region shown, determine (a) Ix and...Ch. 9 - Use integration to find Ix,Iy, and Ixy for the...Ch. 9 - Determine the principal moments of inertia and the...Ch. 9 - The properties of the unequal angle section are...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Chapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... Scores ■Review Determine the maximum constant speed at which the pilot can travel, so that he experiences a maximum acceleration an = 8g = 78.5 m/s². Express your answer to three significant figures and include the appropriate units. μΑ v = Value Units Submit Request Answer Part B ? Determine the normal force he exerts on the seat of the airplane when the plane is traveling at this speed and is at its lowest point. Express your answer to three significant figures and include the appropriate units. о HÅ N = Value Submit Request Answer Provide Feedback ? Units Next >arrow_forwardI want to know the Milankovich orbital element constraint equation. Is it e*cos(i) = cos(argp), where e is eccentricity, i is inclination, and argp is arguement of periapsisarrow_forwardThe following data were taken during a one-hour trial run on a single cylinder, single acting, four-stroke diesel engine of cylinder diameter of 175 mm and stroke 225 mm , the speed being constant at 1000 rpm : Indicated mep: 5.5 barsDiam. of rope brake: 1066 mmLoad on brake: 400 NReading of balance: 27 NFuel consumed: 5.7 kgCalorific value: 44.2 MJ/kg Calculate the indicated power, brake power, specific fuel consumption per indicated kWh and per brake kWh , mechanical efficiency, indicated thermal and brake thermal efficiency.arrow_forward
- mylabmastering.pearson.com Chapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... Document Sharing P Pearson MyLab and Mastering User Settings Part A P Course Home b Success Confirmation of Question Submission | bartleby A particle moves along an Archimedean spiral r = (80) ft, where 0 is given in radians. (Figure 1) If ė = = 4 rad/s and € = 5 rad/s², determine the radial component of the particle's velocity at the instant Express your answer to three significant figures and include the appropriate units. Figure y r = Α ? Vr = Value Units Submit Request Answer Part B Determine the transverse component of the particle's velocity. Express your answer to three significant figures and include the appropriate units. о MÅ ve = Value Submit Request Answer Part C Units ? 1 of 1 Determine the radial component of the particle's acceleration. Express your answer to three significant figures and include the appropriate units. Ar = (80) ft о ΜΑ Value Units ? = π/2 rad.arrow_forwardCan you help me with a matlab code? I am trying to plot the keplerian orbital elements over time. I would usually find the orbit using cartesian system and then transform into keplerian orbital elements. Is there a way to directly integrate keplerian orbital elements?arrow_forwardmylabmastering.pearson.com Chapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... P Pearson MyLab and Mastering Scoresarrow_forward
- K mylabmastering.pearson.com Chapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... P Pearson MyLab and Mastering Mastering Engineering Back to my courses Course Home Scores Course Homearrow_forwardK mylabmastering.pearson.com Chapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... P Pearson MyLab and Mastering Mastering Engineering Back to my courses Course Home Scores Course Homearrow_forwardChapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... Scoresarrow_forwardIn a single cylinder, four stroke, single acting gas engine, the cylinder diameter is 180 mm and the stroke is 350 mm . When running at 250 rpm , the mean area of the indicator diagram taken off the engine is 355 mm² , length of diagram 75 mm , scale of the indicator spring 90 kN/m sq per mm , and the number of explosions was counted to be 114 per minute. Calculate the indicated power. so i have already asked this question and got a good answer, however on step 4, i dont understand how they reached 18.43 KW. When i do the math provided, i get the answer 7195.566. Where am i going wrong? thanks StepsTo clarify how we determined the Indicated Power, I'll go over each step in detail. Step 1: Comprehending the Provided Information - Cylinder diameter (in meters) = 180 mm = 0.18 m - Stroke length (in meters) = 350 mm = 0.35 m - Engine speed = 250 rpm -Indicator diagram mean area = 355 mm² The diagram's length is 75 mm; its spring scale is 90 kN/m² per mm, or 90,000 N/m² per mm; and…arrow_forwardIn MATLAB, can you help me simulate an orbit under earth J2 perturbation with the Milankovich orbital elements? Also, can you check to see if they fit the Milankovich constraint equaiton?arrow_forward8. All of the members in the Warren truss of Figure 8 are of length 10 ft. Use the method of sections to determine the forces in the members BD,CD,CE. B A C D E F G 2000 lb 3000 lb 5000 lb Figure 8 Harrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L

International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Thermodynamics: Maxwell relations proofs 1 (from ; Author: lseinjr1;https://www.youtube.com/watch?v=MNusZ2C3VFw;License: Standard Youtube License