
Interpretation: The continuity equation for the steady incompressible flow in the polar coordinate is to be derived using the mass conservation law.
Concept introduction:
The law of conservation of mass states that mass can only be converted from one form to another, it can neither be created nor destroyed.
The expression of the control volume for mass conservation is,
dA and dV are the area and volume of the small differential part respectively.
v = Velocity of the fluid
The sum of the net rate of mass flux out of control volume and the rate of accumulation of mass in the control volume is zero.
Answer to Problem 9.1P
The expression for the continuity equation in terms of polar coordinates is
Explanation of Solution
The mass flux through the control volume is given as,
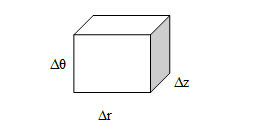
The area of the front surface =
The area of the top surface =
The area of the side surface =
Now, for equation (1), it can be written,
Also,
Substitute equation (2) and equation (3) in equation (1) and use the limit as,
The equation obtained is,
The expression for the continuity equation in terms of polar coordinates is
Want to see more full solutions like this?
Chapter 9 Solutions
Fundamentals of Momentum, Heat and Mass Transfer
- 2. A single-effect evaporator is concentrating a feed solution of organic colloids from 5 to 50 wt %. The solution has a negligible boiling point elevation. The heat capacity of the feed is cp . 4.06 kJ/kg K and the feed enters at 15.6 °C. Saturated steam at 101.32 kPa is available for heating, and the pressure in the vapor space of the evaporator is 15.3 kPa. A total of 4536 kg/h of water is to be evaporated. The overall heat-transfer coefficient is 1988 W/m². K. What is the required surface area in m² and the steam consumption?arrow_forwardA mixture with 4% n-pentane, 40% n-hexane, 50% n-heptane, and 6% n-octane is to be distilled at 14.7 lb/in² (1 atm.) with 98% of the hexane and 1% of the heptane recovered in the distillate. If the liquid feed is a saturated liquid (i.e., q = 1). Calculate i.) The product compositions, ii.) The top and bottom temperature iii.) Minimum reflux ratio (Rm), iv.) Minimum theoretical plates and v.) Actual plates when the reflux ratio is 2Rm. Table 1: Component boiling point and molar mass Component Boiling point n-C5 97°F n-C6 156.2°F n-C7 209.1°F n-C8 258.1°F Molar mass 72.2 86.2 100.2 114.2 Hint: Since 1% of heptane is specified to be recovered in the distillate, 99% of heptane is to be recovered in the bottom.arrow_forwardH.W 1. A plant wishes to dry a certain type of fiberboard. To determine drying characteristics, a sample of 0.3 × 0.3 m with edges sealed was suspended from a balance and exposed to a current of hot dry air. The initial moisture content was 75%. The sheet lost weight at the rate of 1 104 Kg/s unit the moisture content fell to 60%. It was established that the equilibrium moisture content was 10 %. The dry mass of the sample was 0.90 Kg. All moisture contents were on a wet basis. Determine the time for drying the sheets from 75% to 20% moisture under the same drying conditions?arrow_forward
- 2.) A mixture with 4% n-pentane, 40% n-hexane, 50% n-heptane, and 6% n-octane is to be distilled at 14.7 lb/in² with 98% of the hexane and 1% of the heptane recovered in the distillate. If the feed is a saturated liquid (q = 1), the top and bottom temperature are 149°F and 212°F respectively, calculate i.) The product compositions, ii.) Minimum reflux ratio (Rm), iii.) Minimum theoretical plates and iv.) Actual plate when the reflux ratio is 2Rm.arrow_forwardanswer choices 3. A. 0.18, B. 0.44, C. 0.01, D. 2 4. A. 0.2, B. 01, C. 0.4, D. 0.065 5.A. 1.43, B. 5.72, C. 0.93, D. 2.86 6. A. 1.0, B. 4.0, . 2.0, D. 0.65 7.A. 15.5, B. 8.0, C. 11.0, D. 58.5arrow_forwardDescribe with the aid of a labelled diagram how to seperate i) Acetone-water Azeotrope using solvent extractive distillation ii)Acetone-Methano azeotrope using salt effective extractive distillationarrow_forward
- H.W 1. A feed of 4535 kg/h of a 2.0 wt % salt solution at 311 K enters continuously a single-effect evaporator and is being concentrated to 3.0%. The evaporation is at atmospheric pressure and the area of the evaporator is 69.7m². Saturated steam at 383.2 K is supplied for heating. Since the solution is dilute, it can be assumed to have the same boiling point as water. The heat capacity of the feed can be taken as cp = 4.10 kJ/kg K. Calculate the amounts of vapor and liquid product, and the overall heat-transfer coefficient U?arrow_forwardThe switch in Fig.1 has been closed for a long time. It opens at t = Find i(t) for t > 0. 50 www 1.5 H m t=0 10 Ω 9A 0.arrow_forwarde a) 1) Indicate whether each statement below is True or False: Precipitates have a more regular structure than crystals. b) A protein will be more likely to precipitate when the surrounding pH is at its pl. c) Larger proteins are more likely to precipitate than smaller proteins. d) Precipitation nucleation typically follows a secondary nucleation mechanism. e) Precipitates in a CSTR are usually uniform in size. f) Crystallization nucleation usually follows a secondary nucleation mechanism. g) The most common scale-up method for precipitation and crystallization is constant P/V h) Evaporation is commonly carried out above atmospheric pressure. i) The boiling point of a solvent typically rises as the concentration of solute increases. j) Scale-up of evaporation units is usually carried out by increasing evaporator height. k) Unbound water is more difficult to remove than bound water when drying. 1) The most common convection dryer is a freeze dryer. m) Vacuum shelf dryers typically heat…arrow_forward
- 5) Wet insulin crystals containing 32 g water per 100 g of dry insulin need to be dried in air to a moisture level of 5 g water per 100 g of dry insulin. For your convenience, a graph of water content of insulin vs. relative humidity and a psychrometric chart are provided below. a) Determine the percentage of bound and unbound water in the wet crystals before drying. b) Determine the relative humidity of the air to accomplish the drying to 5 g water/100 g dry solids. c) For drying with air at 20°C, what should be the moisture content of the air (g moisture/g dry air)? Water content (g/100 g dry solids) 40 30 20 10 Cefazolin sodium tPA 20 40 Insulin 60 Relative humidity (%) 80 100arrow_forwardA power plant needs to evaporate 1500.0 lbm/h of water at 40.0 °F at 1 atm. Utility superheated steam at 1200 °F and 40 bar is available, but the steam cannot drop below 20 bar and 700 °F. Use the steam tables to determine the specific enthalpies of the four streams. The reference for the enthalpies should be water at the triple point. You may interpolate in Tables B6. and B7, and can also use external, automated sources. Determine the amount of superheated steam required to accomplish the evaporation for a superheated steam outlet of 700 °F and 20 bar. Assume no heat losses and use the steam tables to determine enthalpies.arrow_forwardRecitation 11 Problem 1 400 kg/min of steam enters a steam turbine at 300 °C and 80 bar through a 8.5-cm diameter line and exits at 100 °C and 10.0 bar through a 5.5-cm line. The exiting stream may be vapor, liquid, or "wet steam", a mist composed of saturated water vapor and entrained liquid droplets. Find how much power W (kW) is transferred from the turbine to the steam? The answer can be positive or negative. Neglect AE, but not AEK. What percentage (%) of the total power is due to kinetic energy changes?arrow_forward
 Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
 Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The





