
Find the maximum positive and negative shears and the maximum positive and negative bending moments at point C.
Answer to Problem 6P
The maximum positive shear at point C is
The maximum negative shear at point C is
The maximum positive moment at point C is
The maximum negative moment at point C is
Explanation of Solution
Given Information:
The concentrated live load (P) is 150 kN.
The uniformly distributed live load
The uniformly distributed dead load
Calculation:
Apply a 1 kN unit moving load at a distance of x from left end A.
Sketch the free body diagram of beam as shown in Figure 1.
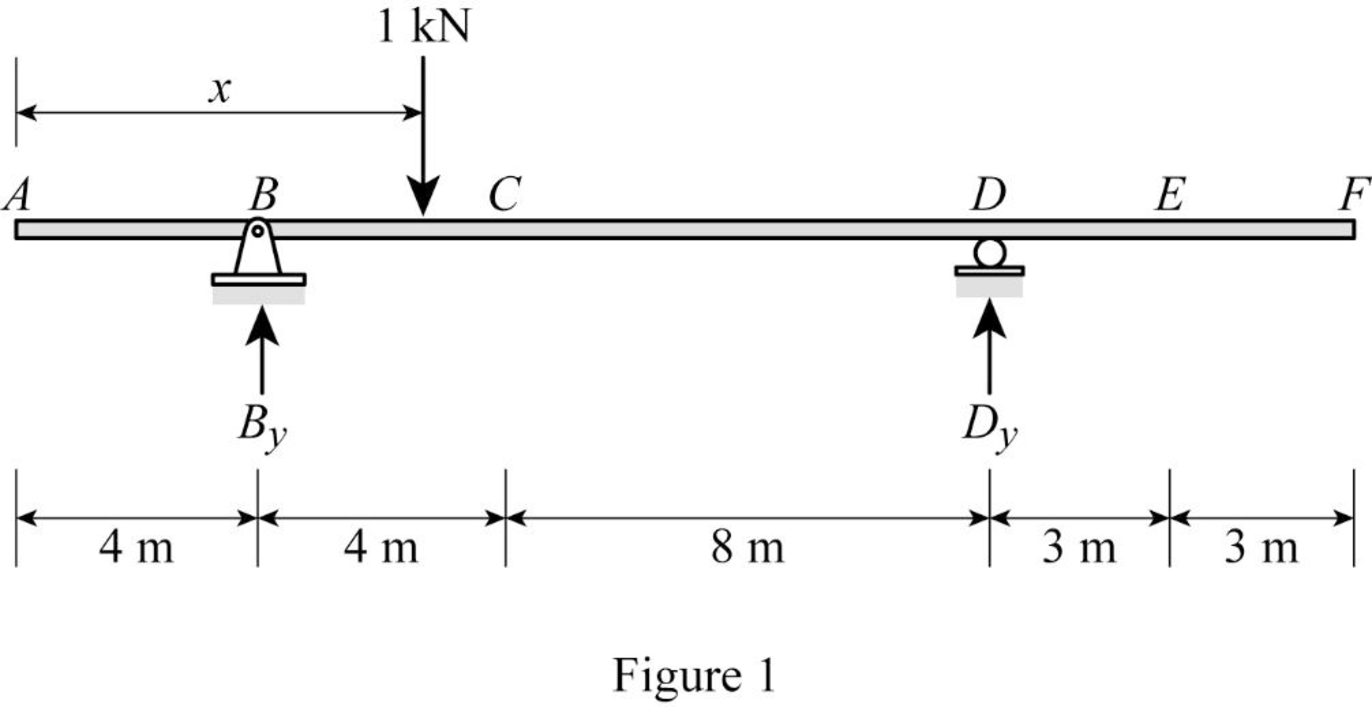
Refer Figure 1.
Find the equation of support reaction
Take moment about point D.
Consider moment equilibrium at point D.
Consider clockwise moment as positive and anticlockwise moment as negative.
Sum of moment at point D is zero.
Find the equation of support reaction
Apply vertical equilibrium equation of forces.
Consider upward force as positive
Substitute
Influence line for the shear at point C.
Apply 1 kN load at just left of C.
Find the equation of shear force at C of portion AB
Sketch the free body diagram of the section AC as shown in Figure 2.

Refer Figure 2.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Apply 1 kN load at just right of C.
Find the equation of shear force at C of portion CF
Sketch the free body diagram of the section AC as shown in Figure 3.
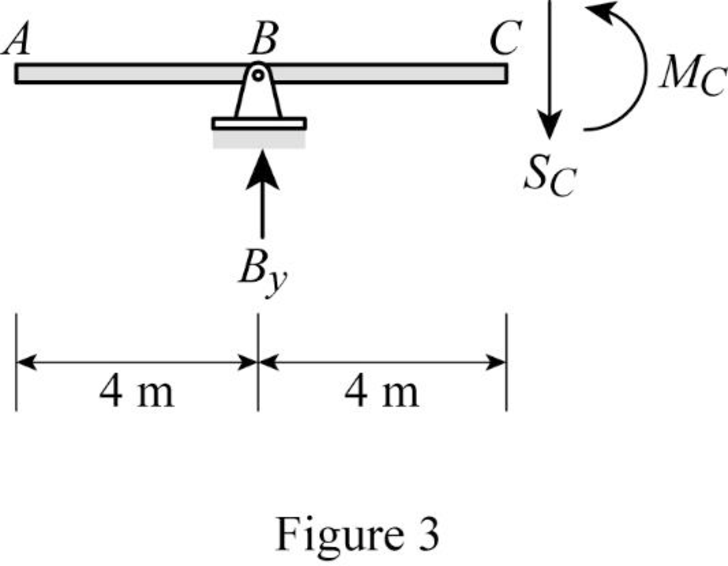
Refer Figure 3.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of shear force
| x | Position | Influence line ordinate of |
| 0 | A | |
| 4 | B | |
| 8 | ||
| 8 | ||
| 16 | D | 0 |
| 19 | E | |
| 22 | F |
Draw the influence lines for the shear force at point C using Table 1 as shown in Figure 4.
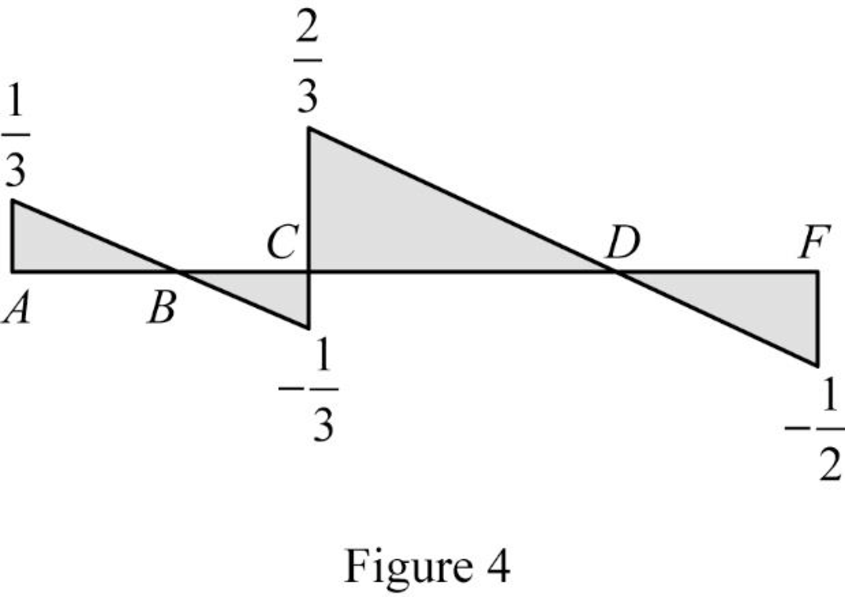
Refer Figure 4.
The maximum positive ILD ordinate at point C is
The maximum negative ILD ordinate at point C is
Find the positive area
Here,
Substitute 4 m for
Find the negative area
Here,
Substitute 4 m for
Find the maximum positive shear at point C using the equation.
Substitute 150 kN for P,
Therefore, the maximum positive shear at point C is
Find the maximum negative shear at point C using the equation.
Substitute 150 kN for P,
Therefore, the maximum negative shear at point C is
Influence line for moment at point C.
Refer Figure 2.
Consider clockwise moment as positive and anticlockwise moment as negative.
Find the equation of moment at C of portion AC
Substitute
Refer Figure 3.
Consider clockwise moment as negative and anticlockwise moment as positive.
Find the equation of moment at C of portion CF
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of moment
| x | Position | Influence line ordinate of |
| 0 | A | |
| 4 | B | 0 |
| 8 | ||
| 16 | D | 0 |
| 19 | E | |
| 22 | F |
Draw the influence lines for the moment at point C using Table 2 as shown in Figure 5.
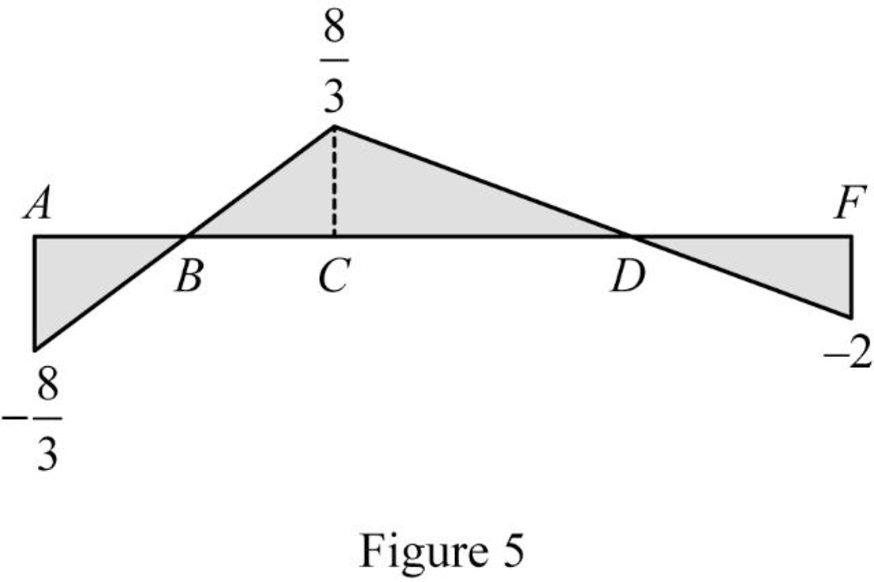
Refer Figure 5.
The maximum positive ILD ordinate of moment at C is
The maximum negative ILD ordinate of moment at C is
Find the positive area
Here,
Substitute 12 m for
Find the negative area
Substitute 4 m for
Find the maximum positive moment at point C using the equation.
Substitute 150 kN for P,
Therefore, the maximum positive moment at point C is
Find the maximum negative moment at point C using the equation.
Substitute 150 kN for P,
Therefore, the maximum negative moment at point C is
Want to see more full solutions like this?
Chapter 9 Solutions
Structural Analysis, Si Edition
- handwritten answers only please. Thank you!arrow_forwardHandwritten answers only please. Thank you!arrow_forwardAn unstretchable cable with mass per unit length 5 kg/m is hanging between points A and B. The horizontal distance between A and B is 20 m. The vertical distance is 15 m (B is in a lower position). We measure a point on the cable which lies by a horizontal distance of 5 meters to point A. It is found to be 4 meters lower than point A. The shape of the cable is almost straight.Use the small sag approximation (Lecture 5) and keep the accuracy to O (e) to estimate the horizontal load H on A and B.arrow_forward
- Q1. For the frame shown below: i. ii. iii. Identify the unknown reactions for the supports (Pin at A and F). Determine if the frame is statically determinate, if not determine the degrees of determinacy. Calculate the unknown reactions for the frames (the frame has internal pin at C) Pin D 25kN 30° 30° 30° 30 B 40kN 60° 16m 60°arrow_forwardQ2. For the beams shown below: i. ii. iii. iv. Sketch the deflected shape Determine the reactions at the supports Calculate and sketch the distribution of the shear force and the bending moment Locate the max moment and POC locations (Note: all dimensions are in meters) 15kN/m 6kN/m 30 KN 30 A B Pin D 5.0 1.0 2.0 3.0arrow_forwardQ2. For the beams shown below: i. ii. iii. iv. Sketch the deflected shape Determine the reactions at the supports Calculate and sketch the distribution of the shear force and the bending moment Locate the max moment and POC locations (Note: all dimensions are in meters) 15kN/m 6kN/m 30 kN 30 Σ A B Pin C D 5.0 1.0 2.0 3.0arrow_forward
- Use Burdine's (1953) equation from the handout (the statistical capillary tube model equation with the values of b, r, and m assumed by Burdine) to mathematically derive a relationship for the hydraulic conductivity function that is based on the SWRC model of Brooks and Corey (1964).arrow_forwardQuestion 2 A sluice gate controls flow in open channels. At sections 1 and 2, the flow is uniform and the pressure is hydrostatic. Neglecting bottom friction and atmospheric pressure, calculate the velocities V1 and V2, and the horizontal force, F, required to hold the gate if h1 = 6m, h2 = 1m, and b = 5m. h₁V₁ Sluice gate, width b Farrow_forwardQuestion 1 A pipeline 30 m long connects two tanks which have a difference of water level of 12 m. The first 10 m of pipeline from the upper tank is of 40 mm diameter and the next 20 m is of 60 mm diameter. At the change of section, a valve is fitted. Calculate the rate of flow when the valve is fully opened assuming that its resistance is negligible and that f for both pipes is 0.0054. In order to restrict the flow the valve is then partially closed. If k for the valve is now 5.6, find the percentage reduction in flow. Note the following Reservoir I Segment of Length Pipeline B Diameter (m) (mm) ABC AB 10 40 BC 20 60 Head loss due to friction h₁ = KQ² Valve fl K = 3.028D' Where, •h₂ = k Head loss due to partial closure (VAB-VBC) 2g Reservoir 2 H-12 marrow_forward
- Civil engineering students performed an evaluation of the two primary methods of classification (supervised and unsupervised). The evaluation of the two methods utilized the error matrices. Tables 1 and 2 represent supervised and unsupervised methods respectively. Reference Data Bare Agriculture Buildings Forest land Agriculture 130 8 44 48 Classified Data Buildings 12 162 10 16 Forest 0 22 170 38 Bare land 8 14 6 180 Table 1 Results of supervised classification 252 + Reference Data Bare Agriculture Buildings Forest land Agriculture 60 16 44 48 Classified Data Buildings 13 80 22 16 Forest 2 35 120 38 Bare land 8 14 6 180 Table 2 Results of unsupervised classification Compare the two methods based on the following parameters: a. User accuracy b. Producer accuracy c. Overall accuracy. d. Explain the above parameters (a, b & c) e. Which one of the two methods has higher accuracy? Justify your answerarrow_forwardThe following figure shows the cross-section of an anchored sheet pile wall. The soil properties and some wall dimensions are shown in the figure and spacing between anchor rods is 2.0 m (center to center). Design the wall using Rankine theory; i.e., calculate the depth of embedment of the wall (D), tensile force on each rodarrow_forwardQ2: A circular concrete culvert of diameter 120 cm carries water of depth 75 cm to irrigate a 30-hectare field. What could be the discharge of this canal if the slope was 0.002? Use Manning's n= 0.014. TWOarrow_forward
