Chapter 9, Problem 52P

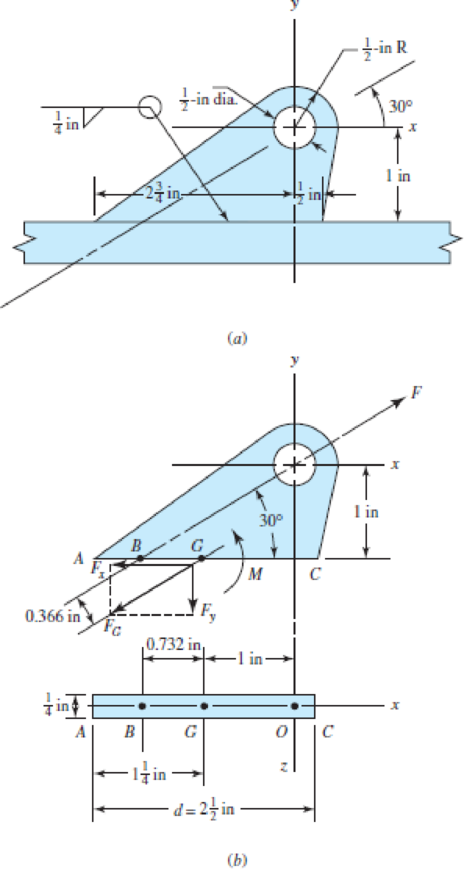
Brackets, such as the one shown, are used in mooring small watercraft. Failure of such brackets is usually caused by bearing pressure of the mooring clip against the side of the hole. Our purpose here is to get an idea of the static and dynamic margins of safety involved. We use a bracket 1/4 in thick made of hot-rolled 1018 steel, welded with an E6010 electrode. We then

assume wave action on the boat will create force F no greater than 1200 lbf.

(a)    Determine the moment M of the force F about the centroid of the weld G. This moment produces a shear stress on the throat resisting bending action with a “tension” at A and “compression” at C.

(b)    Find the force component F_y that produces a shear stress at the throat resisting a “tension” throughout the weld.

(c)    Find the force component F_x that produces an in-line shear throughout the weld.

(d)    Using Table 9–2, determine A, I_u, and I for the bracket.

(e)    Find the shear stress τ₁ at A due to F_y and M, the shear stress τ₂ due to F_x, and combine to find τ.

(f)    Find the factor of safety guarding against shear yielding in the weldment. Since the weld material is comprised of a mix of the electrode material and the base material, take the conservative approach of utilizing the strength of the weaker material.

(g)    Find the factor of safety guarding against a static failure in the parent metal at the weld.

(h)    Assuming the force F alternates between zero and 1200 lbf, find the factor of safety guarding against a fatigue failure in the weld metal using a Gerber failure criterion.

To determine

The moment $M$ of the force $F$ about the centroid of the weld $G$.

Answer to Problem 52P

The moment $M$ of the force $F$ about the centroid of the weld $G$ is $439.2\text{lbf}\cdot \text{in}$.

Explanation of Solution

Write the expression for moment about $A$.

    $M=F\times R$                                                                   (I)

Here, force is $F$ and distance between the centroid and force is $R$.

Conclusion:

Substitute $1200\text{lbf}$ for $F$ and $0.366\text{in}$ for $R$ in Equation (I).

    $\begin{array}{c}M=1200\text{lbf}\times 0.366\text{in}\\ =439.2\text{lbf}\cdot \text{in}\end{array}$

Thus, the moment $M$ of the force $F$ about the centroid of the weld $G$ is $439.2\text{lbf}\cdot \text{in}$.

To determine

The force component $F_y$ that produces a shear stress at the throat resisting a tension throughout the weld.

Answer to Problem 52P

The force component $F_y$ that produces a shear stress at the throat resisting a tension throughout the weld is $600\text{lbf}$.

Explanation of Solution

Write the expression for component of force $F$ along y-direction.

    $F_y=F\sin \theta$                                                                           (II)

Here, force is $F$ and angle between $F$ and y-axis is $\theta$.

Conclusion:

Substitute $1200\text{lbf}$ for $F$ and $30°$ for $\theta$ in Equation (II).

    $\begin{array}{c}{F}_y=1200\text{lbf}\times \sin 30°\\ =1200\text{lbf}\times \text{0}\text{.5}\\ =\text{600}\text{lbf}\end{array}$

Thus, the force component $F_y$ that produces a shear stress at the throat resisting a tension throughout the weld is $600\text{lbf}$.

To determine

The force component $F_x$ that produces an in-line shear throughout the weld.

Answer to Problem 52P

The force component $F_x$ that produces an in-line shear throughout the weld is $1039.2304\text{lbf}$.

Explanation of Solution

Write the expression for component of force $F$ along x-direction.

    $F_x=F\cos \theta$                                                                        (II)

Here, force is $F$ and angle between $F$ and x-axis is $\theta$.

Conclusion:

Substitute $1200\text{lbf}$ for $F$ and $30°$ for $\theta$ in Equation (II).

    $\begin{array}{c}{F}_x=1200\text{lbf}\times \cos 30°\\ =1200\text{lbf}\times \text{0}\text{.866}\\ =\text{1039}\text{.2304}\text{lbf}\end{array}$

Thus, the force component $F_x$ that produces a shear stress at the throat resisting a tension throughout the weld is $\text{1039}\text{.2304}\text{lbf}$.

To determine

The area of throat, unit second moment of area and second area moment by using the Table $9-12$ “Bending properties of fillet welds”.

Answer to Problem 52P

The throat area is $0.972{\text{in}}^2$.

The unit second moment of area is $3.385{\text{in}}^3$.

The second area moment is $0.598{\text{in}}^4$.

Explanation of Solution

Write the expression for throat area.

    $A=1.414h\left(b+d\right)$                                                                         (III)

Here, thickness of weld is $h$, width of weld is $b$ and length of weld is $d$.

Write the expression for unit second moment of area.

    $I_u=\frac{d^2}{6}\left(3b+d\right)$                                                                         (IV)

Here, thickness of weld is $h$, width of weld is $b$ and length of weld is $d$.

Write the expression for second area moment about an axis $G$ parallel to $Z$.

    $I=0.707h{I}_u$                                                                               (V)

Here, thickness of weld is $h$, and unit second moment of area is $I_u$.

Conclusion:

Substitute $0.25\text{in}$ for $h$, $0.25\text{in}$ for $b$ and $2.25\text{in}$ for $d$ in Equation (III).

    $\begin{array}{c}A=1.414\left(0.25\text{in}\right)\left(0.25\text{in}+2.25\text{in}\right)\\ =0.972{\text{in}}^2\end{array}$

Thus, the throat area is $0.972{\text{in}}^2$.

Substitute $0.25\text{in}$ for $h$, $0.25\text{in}$ for $b$ and $2.25\text{in}$ for $d$ in Equation (IV).

    $\begin{array}{c}{I}_u=\frac{{\left(2.25\text{in}\right)}^2}{6}\left(3\left(0.25\text{in}\right)+2.25\text{in}\right)\\ =\frac{{\left(2.25\text{in}\right)}^2}{6}\left(3\text{in}\right)\\ =3.385{\text{in}}^3\end{array}$

Thus, the unit second moment of area is $3.385{\text{in}}^3$.

Substitute $0.25\text{in}$ for $h$ and $3.385{\text{in}}^3$ for $I_u$ in Equation (V).

    $\begin{array}{c}I=0.70\left(70.25\text{in}\right)\left(3.385{\text{in}}^3\right)\\ =0.598{\text{in}}^4\end{array}$

Thus, second area moment is $0.598{\text{in}}^4$.

To determine

The shear stress ${\tau }_1$ at $A$ due to $F_y$.

The shear stress ${\tau }_2$ due to $F_x$.

The combined maximum shear stress $\tau$.

Answer to Problem 52P

The shear stress ${\tau }_1$ at $A$ due to $F_y$ is $617.284\text{psi}$.

The shear stress ${\tau }_2$ due to $F_x$ is $1069.167\text{psi}$.

The maximum shear stress is $1537.158\text{psi}$.

Explanation of Solution

Write the expression for shear stress due to $F_y$.

    ${\tau }_1=\frac{F_y}{A}$                                                                                (VI)

Here, force in y-direction is $F_y$ and the area of cross-section is $A$.

Write the expression for shear stress due to $F_x$.

    ${\tau }_2=\frac{F_x}{A}$                                                                                 (VII)

Here, force in x-direction is $F_x$ and the area of cross-section is $A$.

Write the expression for resultant shear stress at the throat plane.

    ${\tau }^{\prime }=\sqrt{{\left({\tau }_1\right)}^2+{\left({\tau }_2\right)}^2}$                                                                  (VIII)

Here, shear stress due to $F_y$ is ${\tau }_1$ and the shear stress due to $F_x$ is ${\tau }_2$.

Write the expression for secondary shear stress.

    ${{\tau }^{\prime }}^{\prime }=\frac{MC}{I}$                                                                                 (IX)

Here, Moment is $M$, modulus of rigidity is $C$ and the second area moment is $I$.

Write the expression for maximum shear stress.

    ${\tau }_{\max }=\sqrt{{\left({\tau }^{\prime }\right)}^2+{\left({{\tau }^{\prime }}^{\prime }\right)}^2}$                                                                (X)

Here, resultant shear stress at the throat plane is ${\tau }^{\prime }$ and secondary shear stress is ${{\tau }^{\prime }}^{\prime }$.

Conclusion:

Substitute $600\text{lbf}$ for $F_y$ and $0.972{\text{in}}^2$ for $A$ in Equation (VI).

    $\begin{array}{c}{\tau }_1=\frac{600\text{lbf}}{0.972{\text{in}}^2}\\ =617.284\text{psi}\end{array}$

Thus, the shear stress ${\tau }_1$ at $A$ due to $F_y$ is $617.284\text{psi}$.

Substitute $1039.2304\text{lbf}$ for $F_x$ and $0.972{\text{in}}^{\text{2}}$  for $A$ in Equation (VII).

    $\begin{array}{c}{\tau }_2=\frac{1039.2304\text{lbf}}{0.972{\text{in}}^2}\\ =1069.167\text{psi}\end{array}$

Thus, the shear stress ${\tau }_2$ due to $F_x$ is $1069.167\text{psi}$.

Substitute $617.284\text{psi}$ for ${\tau }_1$ and $1069.167\text{psi}$ for ${\tau }_2$ in Equation (VIII).

    $\begin{array}{c}{\tau }^{\prime }=\sqrt{{\left(617.284\text{psi}\right)}^2+{\left(1069.167\text{psi}\right)}^2}\\ =\sqrt{1524157.611}\\ =1234.423\text{psi}\end{array}$

Substitute $439.2\text{lbf}$ for $M$, $1.25\text{psi}$ for $C$ and $0.598{\text{in}}^4$ for $I$ in Equation (IX).

    $\begin{array}{c}{{\tau }^{\prime }}^{\prime }=\frac{439.2\text{lbf}\times 1.25\text{psi}}{0.598{\text{in}}^4}\\ =918.0602\text{psi}\end{array}$

Substitute $1234.423\text{psi}$ for ${\tau }^{\prime }$ and $981.0602\text{psi}$ for $918.0602\text{psi}$ ${{\tau }^{\prime }}^{\prime }$ in Equation (X).

    $\begin{array}{c}{\tau }_{\max }=\sqrt{{\left(1234.423\text{psi}\right)}^2+{\left(918.0602\text{psi}\right)}^2}\\ =\sqrt{2366634.674}\\ =1537.158\text{psi}\end{array}$

Thus, the maximum shear stress is $1537.158\text{psi}$.

To determine

The factor of safety guarding against shear yielding in the weldment.

Answer to Problem 52P

The factor of safety guarding against shear yielding in the weldment is $12$.

Explanation of Solution

Write the expression for factor of safety against guiding against shear yielding in weldment.

    $n=\frac{0.577S_y}{{\tau }_{\max }}$                                                                             (XI)

Here, yield stress is $S_y$ and maximum shear stress is ${\tau }_{\max }$.

Conclusion:

Refer to member of $1080$ HR to obtain yield stress as $32000\text{psi}$ and the ultimate tensile stress as $58000\text{psi}$.

Substitute $32000\text{psi}$ for $S_y$ and $1537.158\text{psi}$ for ${\tau }_{\max }$ in Equation (XI)

    $\begin{array}{c}n=\frac{0.577\left(32000\text{psi}\right)}{1537.158\text{psi}}\\ =12.011\\ \approx 12\end{array}$

Thus, the factor of safety guarding against shear yielding in the weldment is $12$.

To determine

The factor of safety guarding against a static failure in the parent metal at the weld.

Answer to Problem 52P

The factor of safety guarding against a static failure in the parent metal at the weld is $8.5$.

Explanation of Solution

Write the expression for shear stress.

    $\begin{array}{c}\tau =\frac{F_x}{A}\\ =\frac{F}{d\times h}\end{array}$                                                                                  (XII)

Here, force along x-direction is $F_x$, , thickness of weld is $h$  and length of weld is $d$.

Write the expression for normal stress along y-direction.

    ${\sigma }_y=\frac{F_y}{A}+\frac{M}{\left(\frac{I}{C}\right)}$                                                                      (XIII)

Here, force along x-direction is $F_x$, area of cross-section is $A$ moment is $M$, modulus of rigidity is $C$  and second area moment is $I$.

Write the expression for von misses stress theory.

  ${\sigma }^{\prime }=\sqrt{{\sigma }_y^2+3{\tau }^2}$                                                                         (XIV)

Here, normal stress is ${\sigma }_y$ and shear stress is $\tau$.

Write the expression for factor of safety.

    $\left(n\right)=\frac{S_y}{{\sigma }^{\prime }}$                                                                                (XV)

Here, yield stress is $S_y$ and resultant stress ${\sigma }^{\prime }$.

Conclusion:

Substitute $1039.2304\text{lbf}$ for $F_x$, $0.25\text{in}$ for,$h$  and $2.25\text{in}$ for in Equation (XII).

    $\begin{array}{c}\tau =\frac{1039.2304\text{lbf}}{2.25\text{in}\times 0.25\text{in}}\\ =1847.521\text{psi}\end{array}$

Substitute $600\text{lbf}$ for $F_x$, $\left(0.25\times 2.25\right){\text{in}}^2$ for $A$ $439.2\text{lbf}$ for $M$,$0.598{\text{in}}^4$ for $I$ and $1.25\text{psi}$ for $C$ in Equation (XIII).

    $\begin{array}{c}{\sigma }_y=\frac{600\text{lbf}}{\left(0.25\times 2.25\right){\text{in}}^2}+\frac{439.2\text{lbf}}{\left(\frac{0.598{\text{in}}^4}{1.25\text{psi}}\right)}\\ =\left(1066.67\text{psi}\right)+\left(917.64\text{psi}\right)\\ =1984.3\text{psi}\end{array}$

Substitute $1984.3\text{psi}$ for ${\sigma }_y$ and $1847.521\text{psi}$ for $\tau$ in Equation (XIV).

    $\begin{array}{c}{\sigma }^{\prime }=\sqrt{{\left(1984.3\text{psi}\right)}^2+3{\left(1847.521\text{psi}\right)}^2}\\ =\sqrt{3137446.49{\text{psi}}^2}\\ =3765.29\text{psi}\end{array}$

Substitute $32000\text{psi}$ for $S_y$ and $3765.29\text{psi}$ for ${\sigma }^{\prime }$ in Equation (XV).

    $\begin{array}{c}\left(n\right)=\frac{32000\text{psi}}{3765.29\text{psi}}\\ =8.5\end{array}$

Thus, the factor of safety guarding against a static failure in the parent metal at the weld is $8.5$.

To determine

The factor of safety guarding against a fatigue failure in the weld metal using Gerber failure criterion.

Answer to Problem 52P

The factor of safety guarding against a fatigue failure in the weld metal using Gerber failure criterion is $8.11$.

Explanation of Solution

Write the expression for surface factor.

    $\left(K_a\right)=a{\left(S_{ut}\right)}^b$                                                        (XVI)

Here, ultimate tensile strength is $S_{ut}$, $a$ and $b$ are constants.

Write the expression for effective diameter.

    $d_e=0.808\sqrt{0.707hb}$                                              (XVII)

Here, thickness of weld is $h$, and width of weld is $b$.

Write the expression for size factor.

    $k_b={\left(\frac{d_e}{0.3}\right)}^{-0.107}$                                                             (XVIII)

Here, effective diameter is $d_e$.

Write the expression for equivalent strength.

    ${S^{\prime }}_e=0.5S_{ut}$                                                                   (XIX)

Here, ultimate tensile strength is $S_{ut}$.

Write the expression for endurance limit.

    $S_e=k_a{k}_b{k}_c{S^{\prime }}_e$                                                                 (XX)

Here, surface factor is $k_a$, size factor is $k_b$, load factor is $k_c$ and equivalent strength is ${S^{\prime }}_e$.

Write the expression for axial shear stress.

    $\left({\tau }_a\right)=k_{fs}\frac{{\tau }_{\max }}{2}$                                                                (XXI)

Here, surface factor for shear is $k_{fs}$ and maximum shear is ${\tau }_{\max }$.

Write the expression for factor of safety of Gerber criterion.

    $\left(n_f\right)=\frac{1}{2}{\left(\frac{S_{xu}}{{\tau }_a}\right)}^2\left(\frac{{\tau }_a}{S_e}\right)\left\{-1+\sqrt{1+{\left[\frac{2{\tau }_a{S}_e}{S_{xu}{\tau }_a}\right]}^2}\right\}$                (XXII)

Here, maximum shear is ${\tau }_{\max }$, endurance limit is $S_e$ and effective strength is $S_{xu}$.

Conclusion:

Substitute $58\text{kpsi}$ for $S_{ut}$, $14.4$ for $a$ and $-0.718$ for $b$ in Equation XVI).

    $\begin{array}{c}\left(K_a\right)=14.4{\left(58\text{kpsi}\right)}^{-0.718}\\ =14.4\left(0.05418\right)\\ =0.78\end{array}$

Substitute $0.25\text{in}$ for $h$, and $0.25\text{in}$ for $b$ in Equation (XVII).

    $\begin{array}{c}{d}_e=0.808\sqrt{0.707\left(0.25\text{in}\right)\left(0.25\text{in}\right)}\\ =0.808\left(0.209\text{in}\right)\\ =0.169\text{in}\end{array}$

Substitute $0.169\text{in}$ for $d_e$ in Equation (XVIII).

    $\begin{array}{c}{k}_b={\left(\frac{0.169\text{in}}{0.3}\right)}^{-0.107}\\ ={\left(0.5633\right)}^{-0.107}\\ =1.06\end{array}$

Substitute $58\text{kpsi}$ for $S_{ut}$ in Equation (XIX).

    $\begin{array}{c}{S^{\prime }}_e=0.5\left(58\text{kpsi}\right)\\ =29\text{kpsi}\end{array}$

Substitute $0.780$ for $k_a$, $1.06$ for $k_b$, $0.59$ for $k_c$ and $29\text{kpsi}$ for ${S^{\prime }}_e$ in Equation (XX).

    $\begin{array}{c}{S}_e=\left(0.780\right)\left(1.06\right)\left(0.59\right)\left(29\text{kpsi}\right)\\ =14.14\text{kpsi}\end{array}$

Substitute $2.7$ for $k_{fs}$ and $1.537\text{kpsi}$ for ${\tau }_{\max }$ in Equation (XXI).

    $\begin{array}{c}\left({\tau }_a\right)=2.7\times \frac{1.537\text{kpsi}}{2}\\ =2.07\text{kpsi}\end{array}$

Substitute $0.67\left(58\text{kpsi}\right)$ for $S_{xu}$, $2.07\text{kpsi}$ for ${\tau }_a$, $14.14\text{kpsi}$ for $S_e$ in Equation (XXII).

    $\begin{array}{c}\left(n_f\right)=\frac{1}{2}{\left(\frac{0.67\left(58\text{kpsi}\right)}{2.07\text{kpsi}}\right)}^2\left(\frac{2.07\text{kpsi}}{14.14\text{kpsi}}\right)\left\{-1+\sqrt{1+{\left[\frac{2\left(2.07\text{kpsi}\right)\left(14.14\text{kpsi}\right)}{\left(0.67\left(58\text{kpsi}\right)\right)2.07\text{kpsi}}\right]}^2}\right\}\\ =176.21\times \left(0.14639\right)\left\{0.3144\right\}\\ =8.11\end{array}$

Thus, the factor of safety guarding against a fatigue failure in the weld metal using Gerber failure criterion is $8.11$.