
Concept explainers
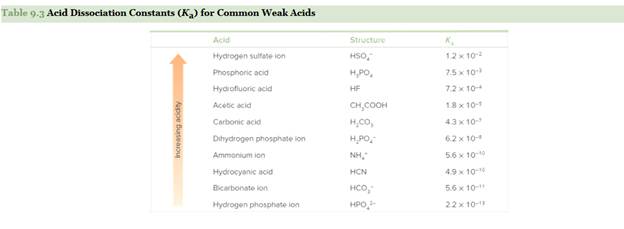
Use the data in and 9.2 and 9.3 to label the stronger acid in each pair. Which acid in each pair hasthe stronger conjugate base?
a.
b.
c.
Table 9.2 Relative Strength of Acids and Their Conjugate Bases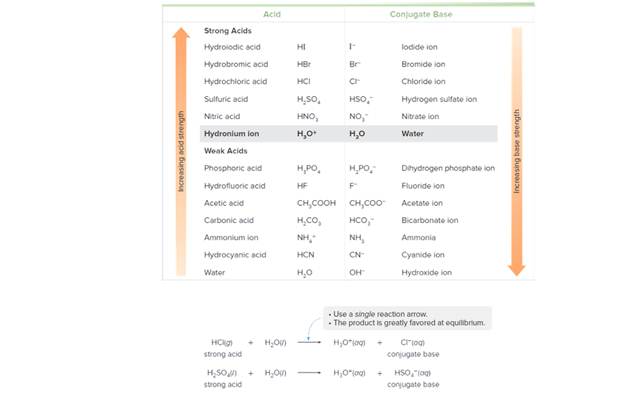 Table 9.3 Acid Dissociation Constants
Table 9.3 Acid Dissociation Constants
Want to see the full answer?
Check out a sample textbook solution
Chapter 9 Solutions
Loose Leaf for General, Organic and Biological Chemistry with Connect 2 Year Access Card
- Please correct answer and don't used hand raiting and don't used Ai solutionarrow_forwardPlease correct answer and don't used hand raitingarrow_forwardThe vibrational contribution isa) temperature independent for internal energy and heat capacityb) temperature dependent for internal energy and heat capacityc) temperature independent for heat capacityd) temperature independent for internal energyarrow_forward
- Quantum mechanics. Explain the basis of approximating the summation to an integral in translational motion.arrow_forwardQuantum mechanics. In translational motion, the summation is replaced by an integral when evaluating the partition function. This is correct becausea) the spacing of the translational energy levels is very small compared to the product kTb) the spacing of the translational energy levels is comparable to the product kTc) the spacing of the translational energy levels is very large compared to the product kTarrow_forwardDon't used Ai solutionarrow_forward
- Please correct answer and don't used hand raiting don't used Ai solutionarrow_forwardIf the viscosity of hydrogen gas (at 0oC and 1 atm) is 8.83x10-5 P. If we assume that the molecular sizes are equal, calculate the viscosity of a gas composed of deuterium.arrow_forwardIf the viscosity of hydrogen gas (at 0oC and 1 atm) is 8.83x10-5 P. If we assume that the molecular sizes are equal, calculate the viscosity of a gas composed of deuterium.arrow_forward
- Laser. Indicate the relationship between metastable state and stimulated emission.arrow_forwardThe table includes macrostates characterized by 4 energy levels (&) that are equally spaced but with different degrees of occupation. a) Calculate the energy of all the macrostates (in joules). See if they all have the same energy and number of particles. b) Calculate the macrostate that is most likely to exist. For this macrostate, show that the population of the levels is consistent with the Boltzmann distribution. macrostate 1 macrostate 2 macrostate 3 ε/k (K) Populations Populations Populations 300 5 3 4 200 7 9 8 100 15 17 16 0 33 31 32 DATO: k = 1,38×10-23 J K-1arrow_forwardDon't used Ai solutionarrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
 Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Chemistry by OpenStax (2015-05-04)ChemistryISBN:9781938168390Author:Klaus Theopold, Richard H Langley, Paul Flowers, William R. Robinson, Mark BlaserPublisher:OpenStax
Chemistry by OpenStax (2015-05-04)ChemistryISBN:9781938168390Author:Klaus Theopold, Richard H Langley, Paul Flowers, William R. Robinson, Mark BlaserPublisher:OpenStax Organic Chemistry: A Guided InquiryChemistryISBN:9780618974122Author:Andrei StraumanisPublisher:Cengage Learning
Organic Chemistry: A Guided InquiryChemistryISBN:9780618974122Author:Andrei StraumanisPublisher:Cengage Learning





