Find the maximum negative bending moment at point B.
Answer to Problem 1P
The maximum negative bending moment at point B is
Explanation of Solution
Given Information:
The concentrated live load (P) is 75 kN.
Calculation:
Apply a 1 kN unit moving load at a distance of x from left end A.
Sketch the free body diagram of beam as shown in Figure 1.
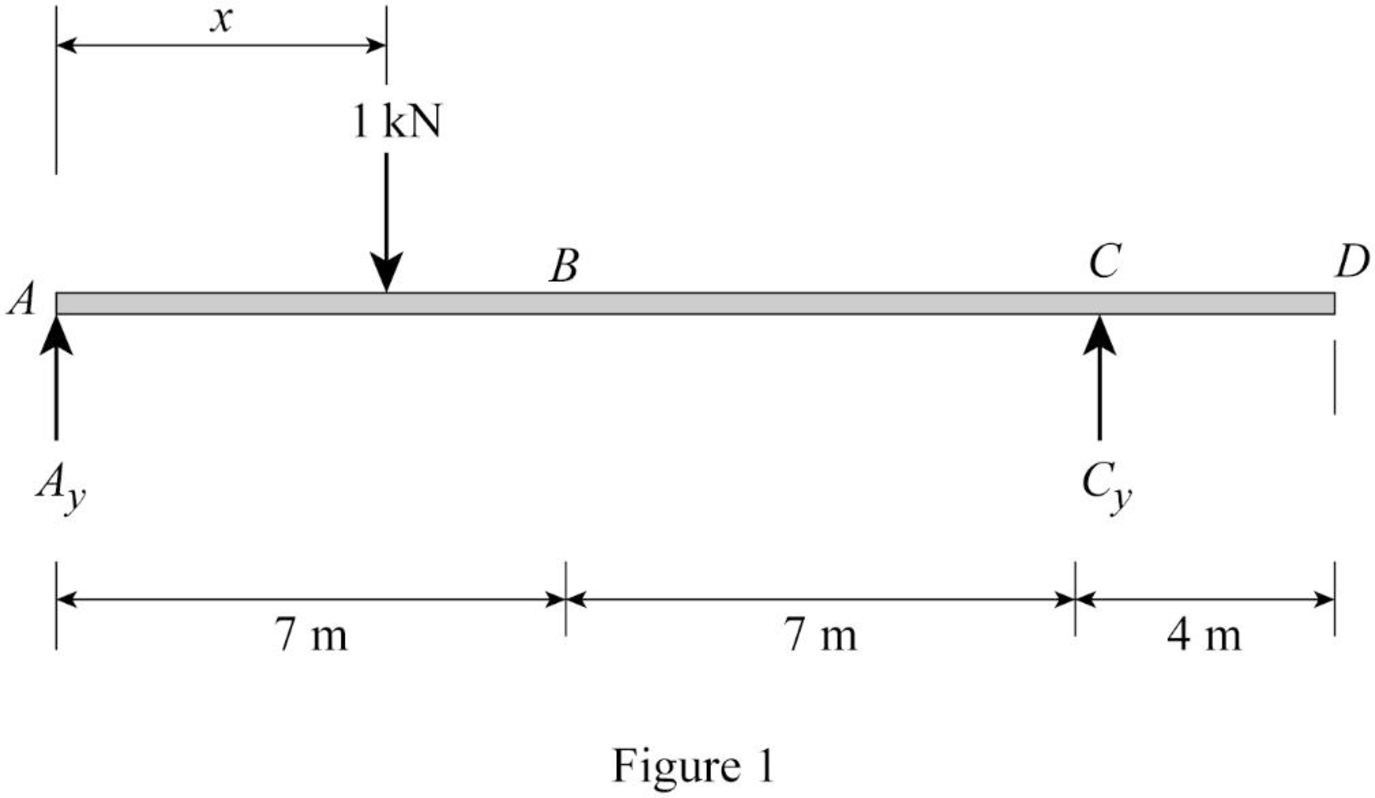
Refer Figure 1.
Find the equation of support reaction
Take moment about point A.
Consider moment equilibrium at point A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Sum of moment at point A is zero.
Find the equation of support reaction
Apply vertical equilibrium equation of forces.
Consider upward force as positive
Substitute
Find the equation of moment at B.
Apply 1 kN at just left of B
Sketch the free body diagram of the section AB as shown in Figure 2.
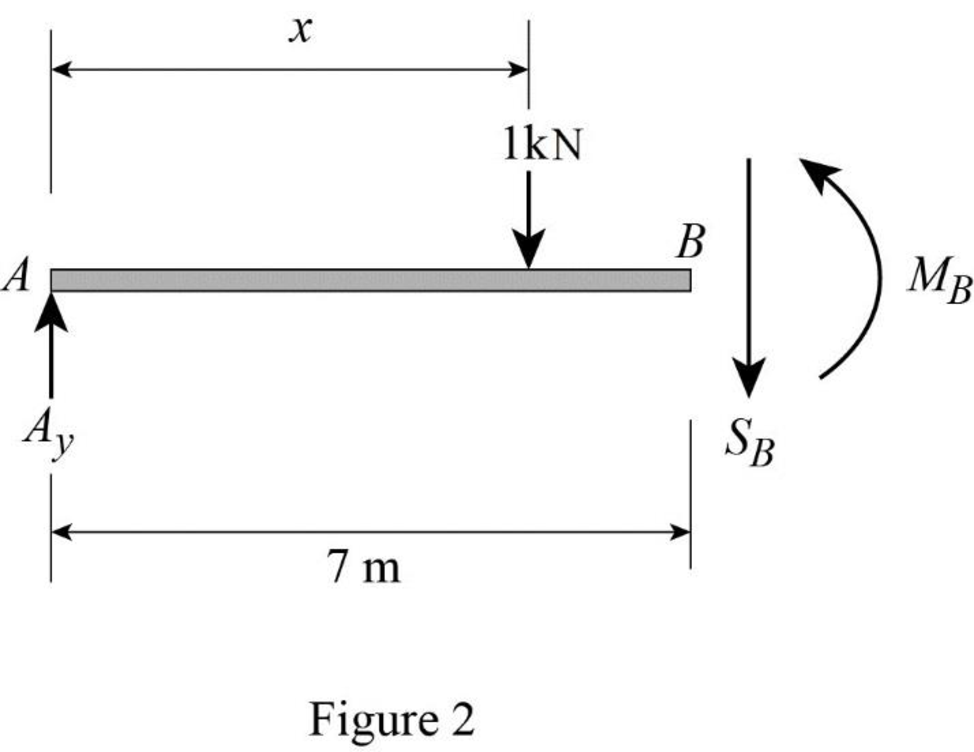
Refer Figure 2.
Consider moment at B.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Apply 1 kN at just right of B
Sketch the free body diagram of the section BD as shown in Figure 3.
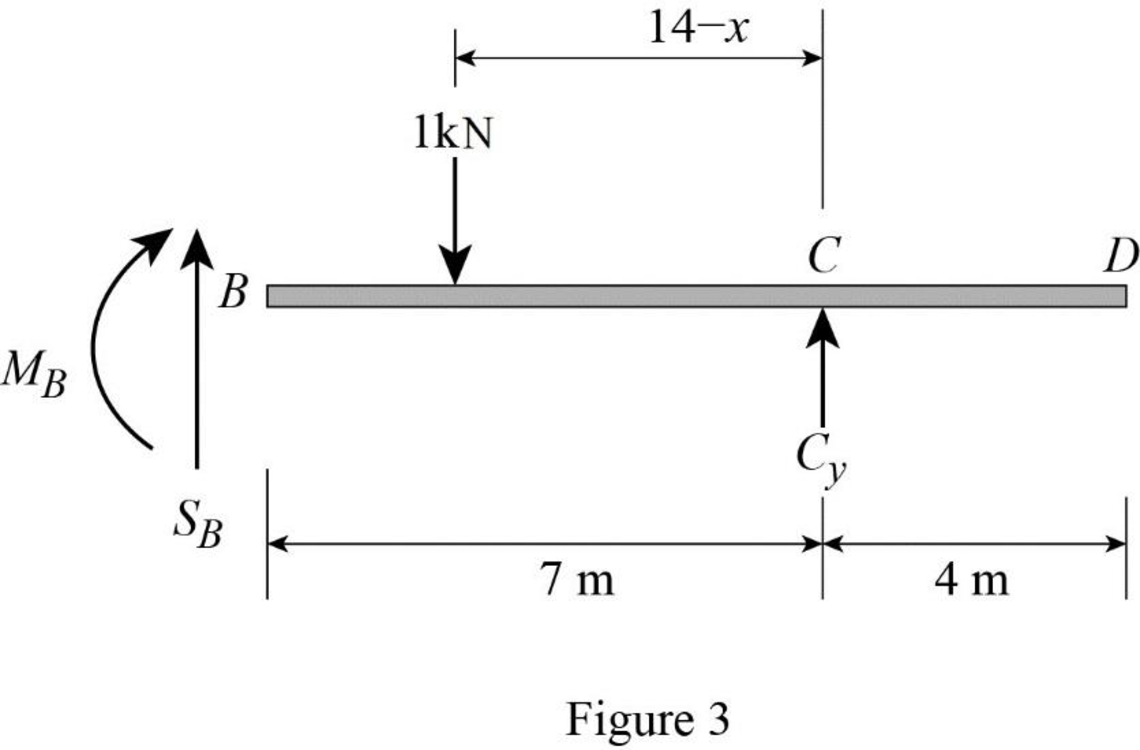
Refer Figure 3.
Consider moment at B.
Consider clockwise moment as positive and anticlockwise moment as negative.
Find the equation of moment at B of portion BC
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of moment at various points of x using the Equations (3) and (4) and summarize the value as in Table 1.
| x | |
| 0 | 0 |
| 7 | |
| 14 | 0 |
| 28 | –2 |
Draw the influence lines for the moment at point B using Table 4 as shown in Figure 4.
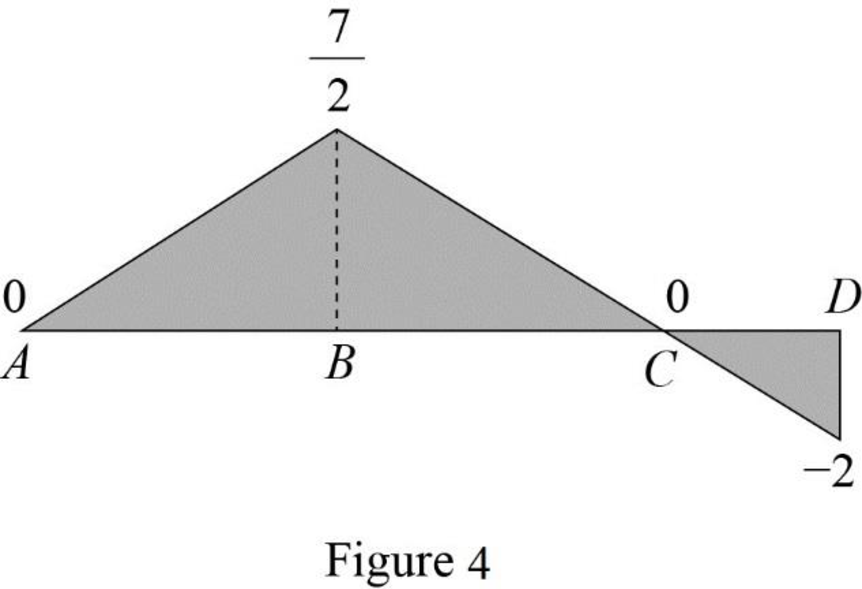
Refer Figure 4,
The maximum negative influence line ordinate of bending moment at B is
Find the maximum negative bending moment at point B using the equation.
Substitute 75 kN for P and
Therefore, the maximum negative bending moment at point B is
Want to see more full solutions like this?
Chapter 9 Solutions
Structural Analysis, SI Edition
- Consider the following figure: H/3 Pa Given: H = 7 m, y = 13 kN/m³, ø′ = 25°, c′ = 12 kN/m², and a = 10°. For given values, K₁ = 0.296. Calculate the Rankine active force per unit length of the wall after the occurrence of the tensile crack. (Enter your answer to three significant figures.) Pa = kN/marrow_forwardWall movement to left 45+ '/2 45 + 6'/2 Rotation of wall about this point A vertical retaining wall shown in the figure above is 7 m high with a horizontal backfill. For the backfill, assume that y = 14.5 kN/m³, ' = 26°, and c′ = 18 kN/m². Determine the Rankine active force per unit length of the wall after the occurrence of the tensile crack. (Enter your answer to three significant figures.) Pa = kN/marrow_forwardConsider the following figure: 0.6 "d 0.5 k₁ = 0 0.4 03 =0 kh = 0.2 0.3 0.025 0.2 0.05 0.1 0.1 0.2 0 -0.1 ↓ 0 5 10 15 20 25 30 35 40 45 ' (deg) For a retaining wall with a vertical back and horizontal backfill with a c'-' soil, the following are given: H = 10 ft Y = 111 lb/ft³ ' = 25° kh = 0.2 k₁ = 0 c = 113 lb/ft² Determine the magnitude of active force Pae on the wall. (Enter your answer to two significant figures.) Pae = lb/ftarrow_forward
- A 13.0 ft high vertical wall retains an overconsolidated soil where OCR = 1.5, c' = 0, and ' magnitude and the location of the horizontal load on the wall, assuming the at-rest condition. Use Ysat (Enter your answers to three significant figures.) 33°. If the entire soil behind the wall is submerged with the water level at the ground surface, determine the 127 lb/ft³. Activity Frame P₁ = lb/ft Height above the bottom of the wall = O Icon Kov ftarrow_forward= A 5 m high smooth vertical wall retains a clay backfill with c = 13 kN/m², ' -25°, and y = 17.0 kN/m³. The clay is in active state. a. Determine the maximum tensile stress within the clay. (Enter your answer to three significant figures.) σα = kN/m² b. Determine the depth of the tensile cracks. (Enter your answer to three significant figures.) Zo = m c. Determine the magnitude and location of the active thrust, neglecting the tensile zone. (Enter your answers to three significant figures.) Pa x = = kN/m² marrow_forwardA composite beam is fabricated by bolting two 3.1-in.-wide by 14-in.-deep timber planks to the sides of a 0.4-in. by 14-in. steel plate. The moduli of elasticity of the timber and the steel are 1940 ksi and 30300 ksi, respectively. The simply supported beam spans a distance of 21 ft and carries two concentrated loads P, which are applied as shown. Assume LAB = LCD = 5 ft, Lgc = 11 ft, b = 3.1 in., d = 14 in. and t = 0.4 in. (a) Determine the maximum bending stresses σ,, σ, produced in the timber planks and the steel plate if P = 2.1 kips. (b) Assume that the allowable bending stresses of the timber and the steel are 830 psi and 24900 psi, respectively. Determine the largest acceptable magnitude for concentrated loads P. (You may neglect the weight of the beam in your calculations.) LAB B Answers: LCD LBC b Cross section D ksi, σ, = i ksi. (a) σ, = (b) P= i i kips.arrow_forward
- The internal shear force at a certain section of a steel beam is V = 107 kips. If the beam has the cross section shown, determine the shear stress at point H, which is located 2 in. below the top surface of the flanged shape. The centroid is 5.283 in. above the bottom surface of the beam, and the moment of inertia about the z axis is 465.8 in.4. 5 in. 2 in. H 业 1 in. 1 in. 12 in. 8 in. 1 in. 11.51 ksi O 9.72 ksi 8.34 ksi 6.03 ksi ○ 7.73 ksiarrow_forwardThe beam shown will be constructed from a standard steel W-shape using an allowable bending stress of 33.6 ksi. Assume P = 70 kips. L₁ = 2.2 ft, and L2 = 6.6 ft. (a) Determine the minimum section modulus required for this beam. (b) From the table below, select the lightest W shape that can be used for this beam. (c) What is the total weight of the steel beam itself (ie, not including the loads that are carried by the beam)? Lu B D L2 L₁ Wide-Flange Sections or W Shapes-U.S. Customary Units x x be Web Area Depth thickness Flange width Flange thickness Designation A d Tw by 4 S₁ و" in.² in. in. in. in. in,4 in.³ in. in.4 in,³ in. W24 x 94 27.7 24.3 0.515 9.07 0.875 2700 222 9.87 109 24.0 1.98 24 x 76 22.4 23.9 0.440 8.99 0.680 2100 176 9.69 82.5 18.4 1.92 24 x 68 20.1 23.7 0.415 8.97 0.585 1830 154 9.55 70.4 15.7 1.87 24 x 55 16.2 23.6 0.395 7.01 0.505 1350 114 9.11 29.1 8.30 1.34 W21 x 68 20.0 21.1 0.430 8.27 0.685 1480 140 8.60 64.7 15.7 1.80 21 x 62 18.3 21.0 0.400 8.24 0.615 1330 127…arrow_forwardA composite beam is made of two brass [E=114 GPa] bars bonded to two aluminum [E = 74 GPa] bars, as shown. The beam is subjected to a bending moment of 335 N-m acting about the z axis. Using a = 5 mm, b = 30 mm, c = 10 mm, and d = 20 mm, calculate (a) the maximum bending stress in the aluminum bars. (b) the maximum bending stress in the brass bars. N Aluminum C Brass Brass Aluminum b Answers: (a) σal= (b) Obr= a a MPa MPaarrow_forward
- A standard steel pipe (D = 3.500 in.; d = 3.068 in.) supports a concentrated load of P = 630 lb as shown. The span length of the cantilever beam is L = 4 ft. Determine the magnitude of the maximum horizontal shear stress in the pipe. 720 psi 761 psi 508 psi 564 psi 667 psi L Pipe cross section.arrow_forwardA beam is subjected to equal bending moments of M₂ = 59 kip-ft. The cross-sectional dimensions are b₁ = 7.5 in., d₁ = 1.4 in., b₂ = 0.55 in., d₂ = 5.0 in., b3 = 3.2 in., and d3 = 1.5 in. Determine: (a) the centroid location (measured with respect to the bottom of the cross-section), the moment of inertia about the z axis, and the controlling section modulus about the z axis. (b) the bending stress at point H. Tensile stress is positive, while compressive stress is negative. (c) the bending stress at point K. Tensile stress is positive, while compressive stress is negative. (d) the maximum bending stress produced in the cross section. Tensile stress is positive, while compressive stress is negative. M₂ Z M₂ Answer: (a) y= i Iz= in. in.4 S= i on,3 (b) σH= i ksi (c) OK = i ksi (d) σmax= ksi K b₁ d₁ H b₂ b3 d₂ d3arrow_forwardA cantilever timber beam with a span of L = 2.9 m supports a uniformly distributed load w. The beam width is b = 300 mm and the beam height is h = 160 mm. The allowable bending stress of the wood is 7 MPa. Determine the magnitude of the maximum load w that may be carried by the beam. Answer: w= I i kN/m.arrow_forward
