
Find maximum positive shear and bending moment at point B due to the series of four moving concentrated loads
Explanation of Solution
Calculation:
Apply a 1 k unit moving load at a distance of x from left end A.
Sketch the free body diagram of beam as shown in Figure 1.
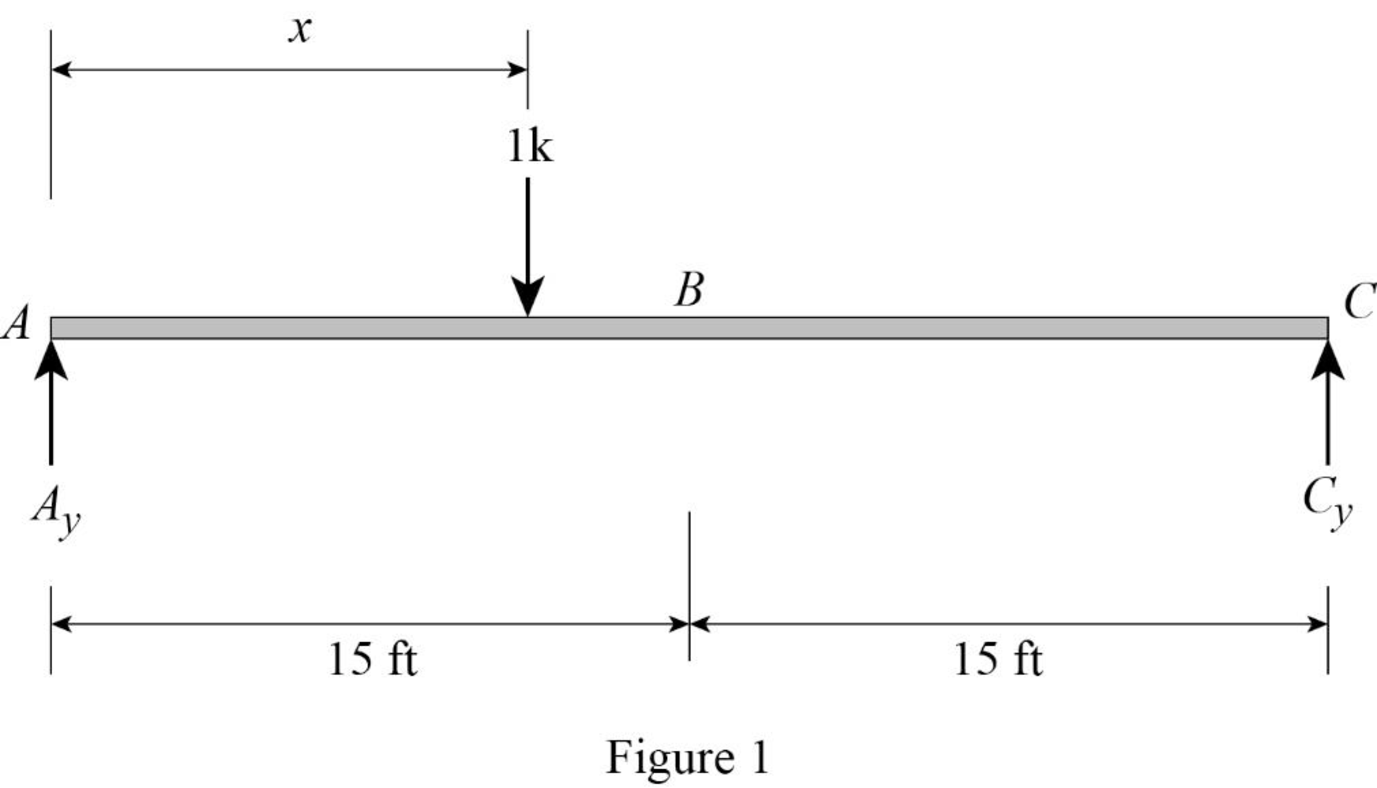
Refer Figure 1.
Find the equation of support reaction
Take moment about point C.
Consider moment equilibrium at point C.
Consider clockwise moment as positive and anticlockwise moment as negative.
Sum of moment at point C is zero.
Find the equation of support reaction
Apply vertical equilibrium equation of forces.
Consider upward force as positive
Substitute
Influence line for shear at B.
Find the equation of shear force at B of portion AB
Sketch the free body diagram of the section AB as shown in Figure 2.
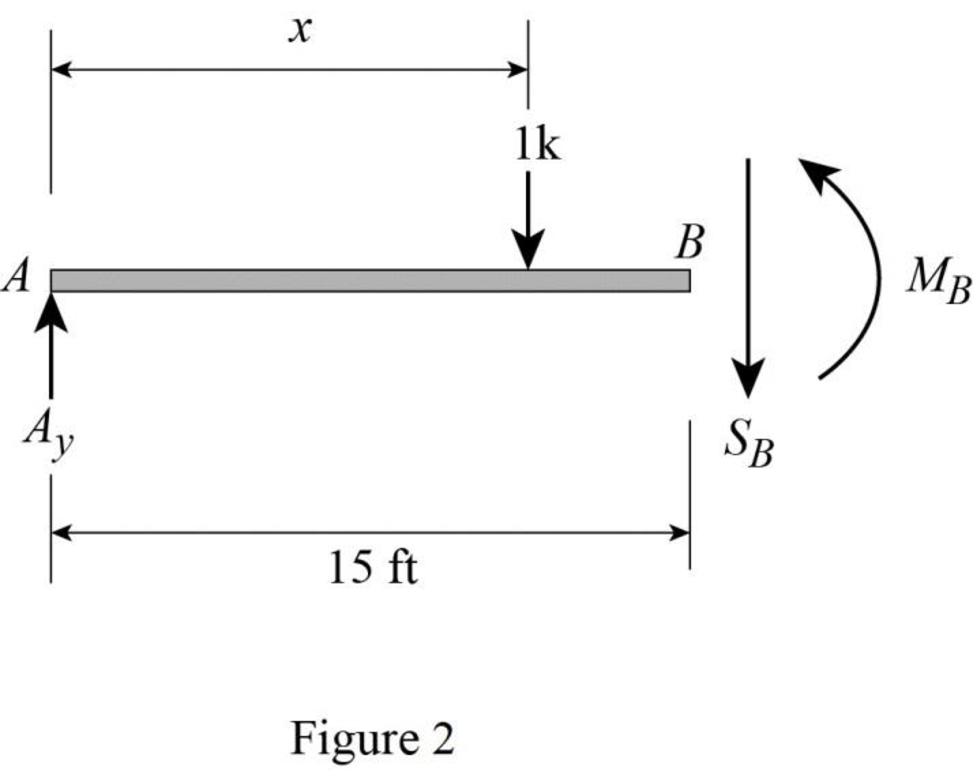
Refer Figure 2.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Find the equation of shear force at B of portion BC
Sketch the free body diagram of the section BC as shown in Figure 3.
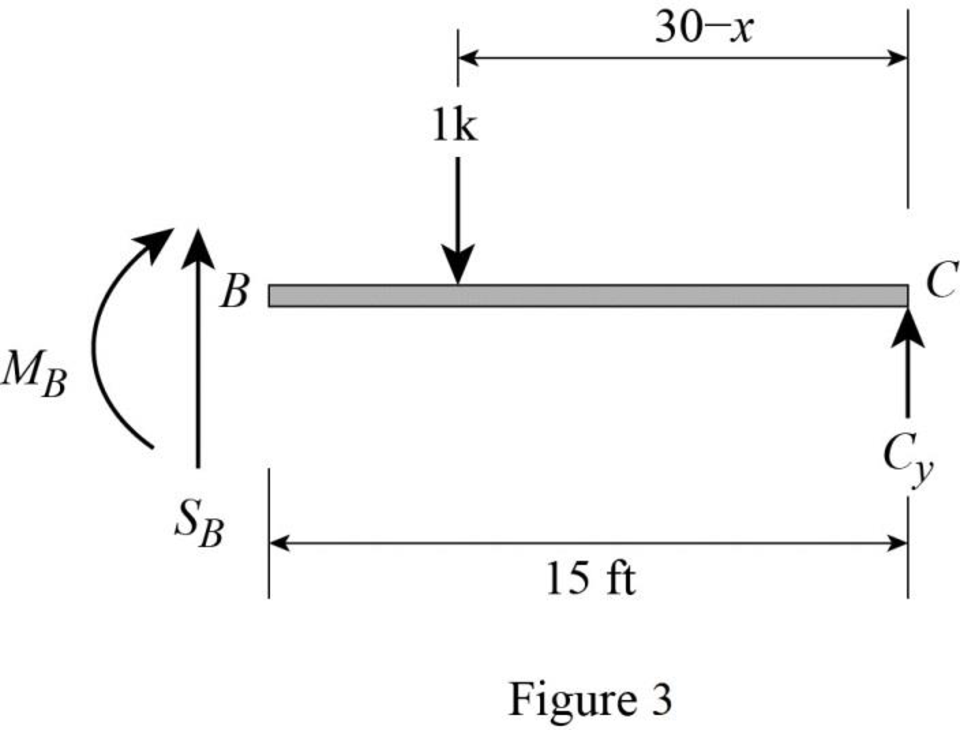
Refer Figure 3.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of shear force at various points of x using the Equations (3) and (4) and summarize the value as in Table 1.
| x | |
| 0 | 1 |
| 30 | 0 |
Draw the influence lines for the shear force at point B using Table 1 as shown in Figure 4.
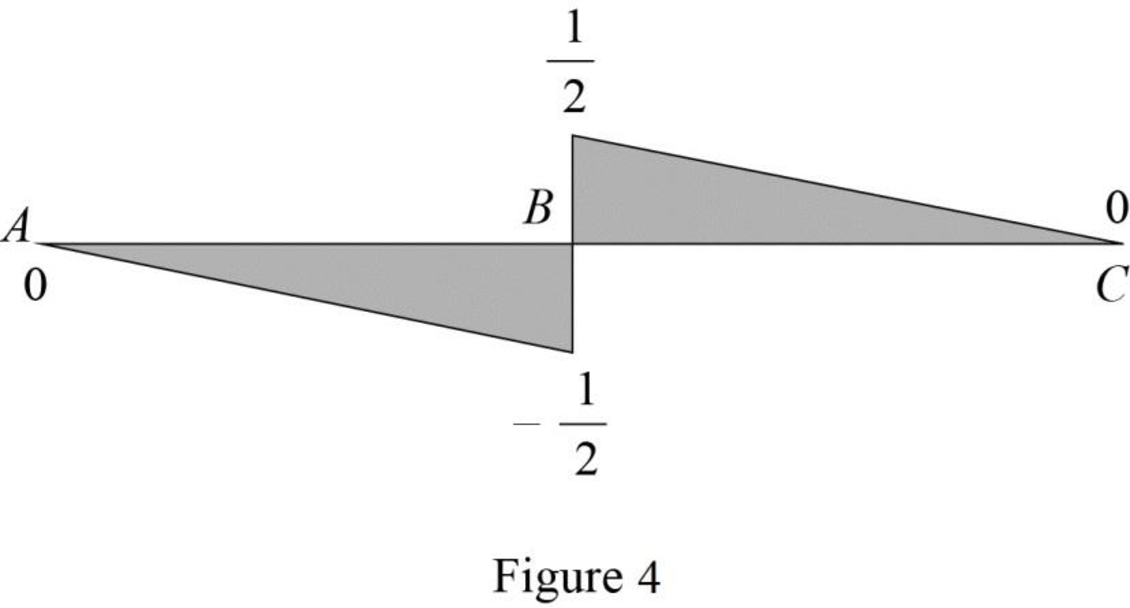
Refer Figure 4.
Find the slope
Here,
Substitute 15 ft for
Find the slope
Here,
Substitute 15 ft for
Sketch the loading position as shown in Figure 5.
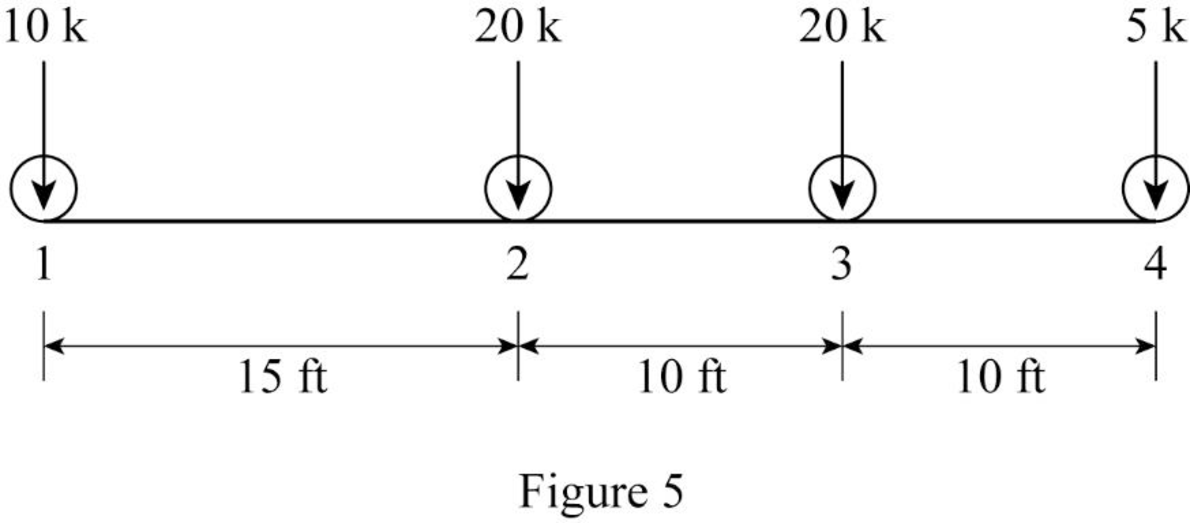
Find the maximum positive shear force at B.
Sketch the loading position on the beam when the load 1 placed at just right of B as shown in Figure 6.
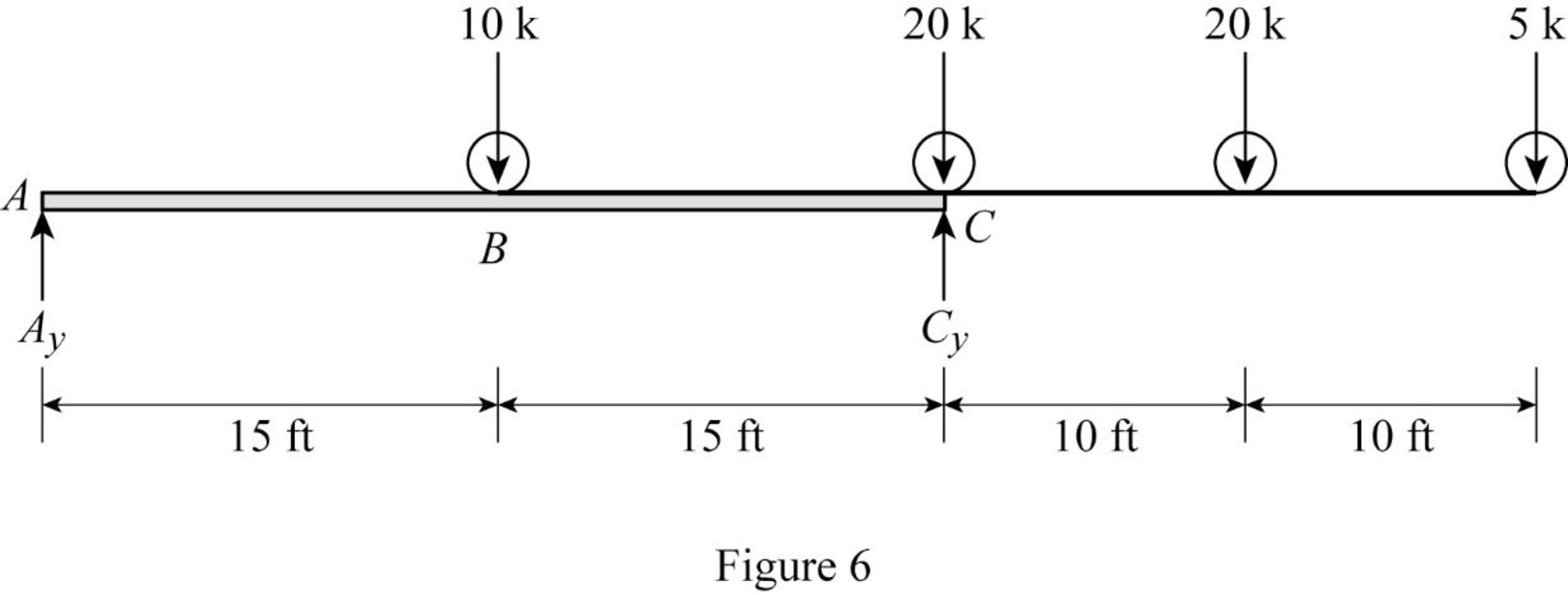
Refer Figure 6.
Find the shear force at B when the load 1 placed at just right of B.
Substitute 15 ft for
Sketch the loading position on the beam when the load 2 placed at just right of B as shown in Figure 7.
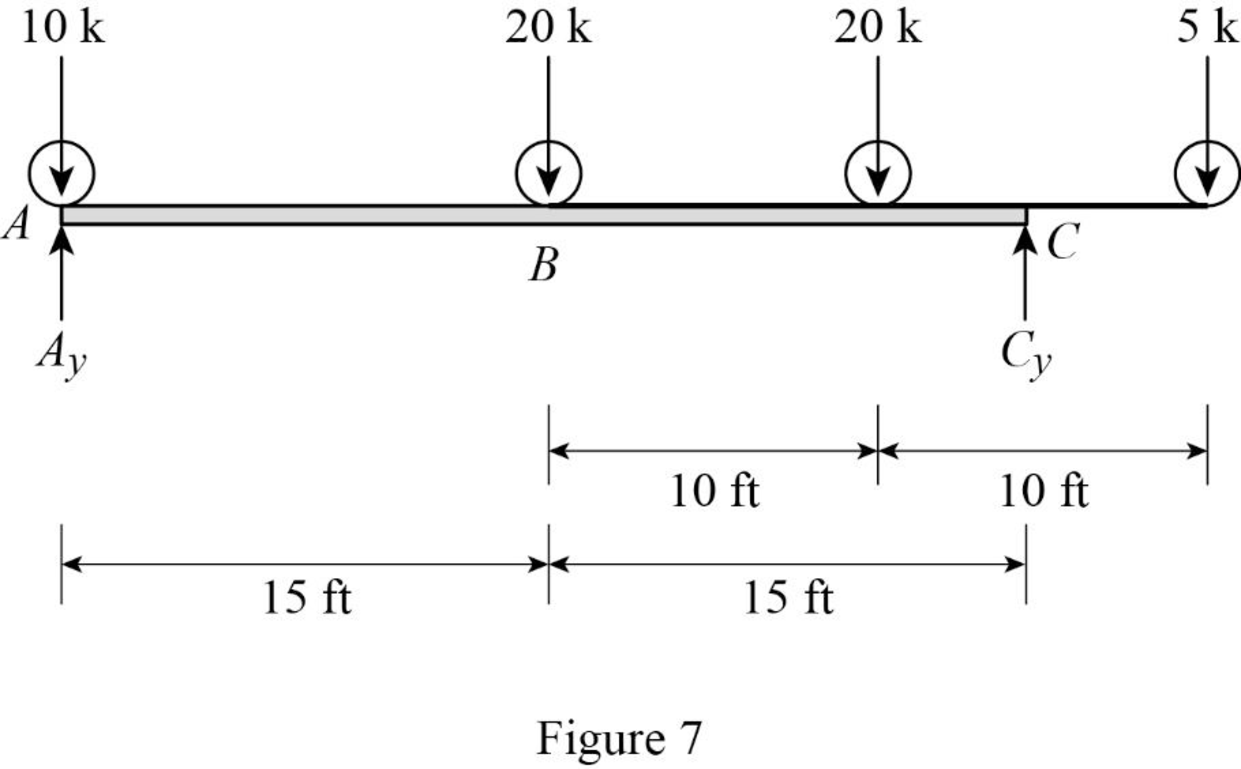
Refer Figure 7.
Find the shear force at B when the load 2 placed at just right of B.
Substitute 15 ft for
Sketch the loading position on the beam when the load 3 placed at just right of B as shown in Figure 8.
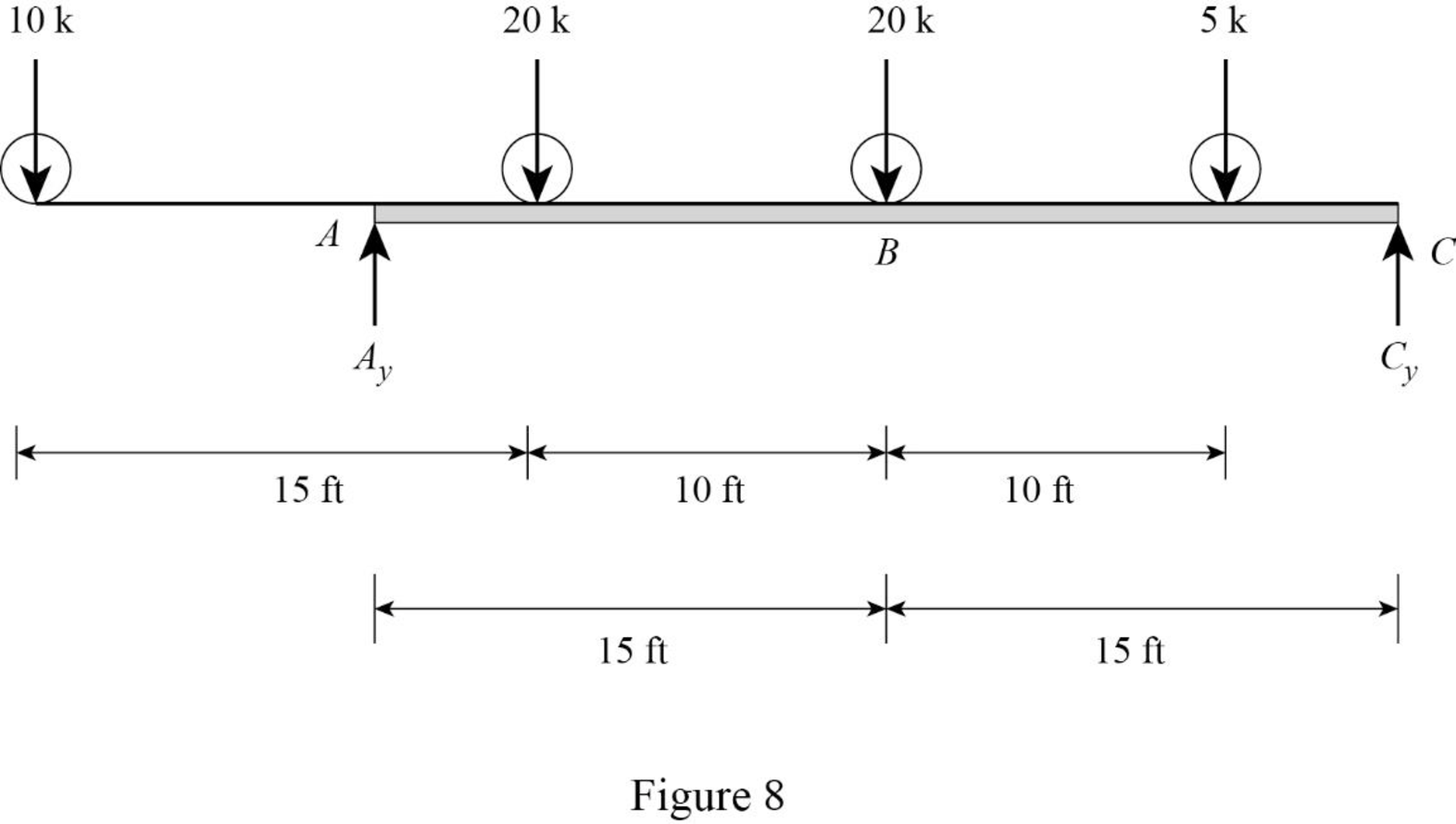
Refer Figure 8.
Find the shear force at B when the load 3 placed at just right of B.
Substitute 15 ft for
Sketch the loading position on the beam when the load 4 placed at just right of B as shown in Figure 9.
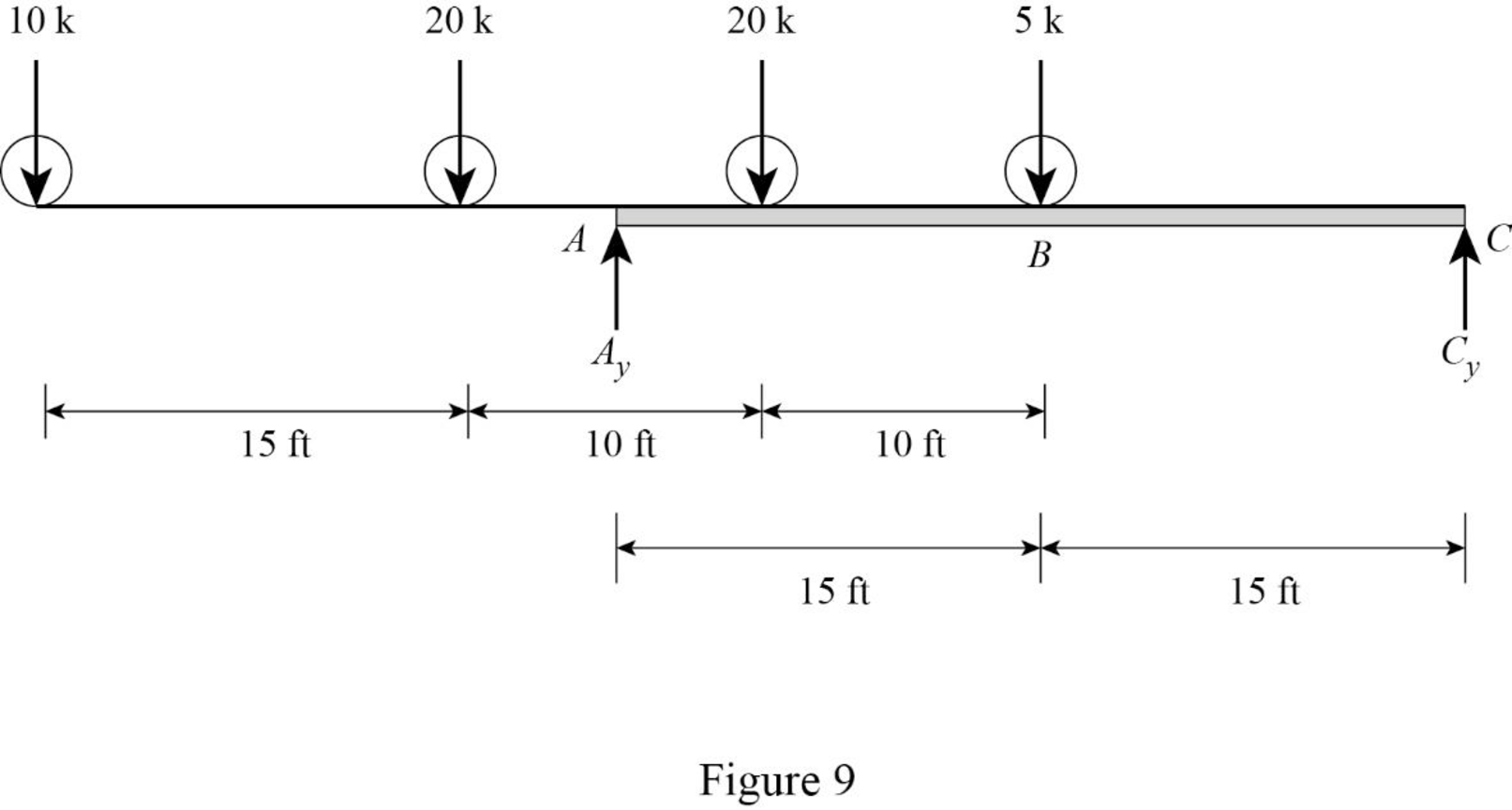
Refer Figure 9.
Find the shear force at B when the load 3 placed at just right of B.
Substitute 15 ft for
Maximum positive shear force at B as follows.
The maximum positive shear at B is the maximum of
Therefore, the maximum positive shear at point B is
Influence line for moment at B.
Refer Figure 2.
Consider clockwise moment as positive and anticlockwise moment as negative.
Find the equation of moment at B of portion AB
Substitute
Refer Figure 3.
Consider clockwise moment as negative and anticlockwise moment as positive.
Find the equation of moment at B of portion BC
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of moment at various points of x using the Equations (5) and (6) and summarize the value as in Table 2.
| x | |
| 0 | 0 |
| 30 | 0 |
Draw the influence lines for the moment at point B using Table 2 as shown in Figure 10.
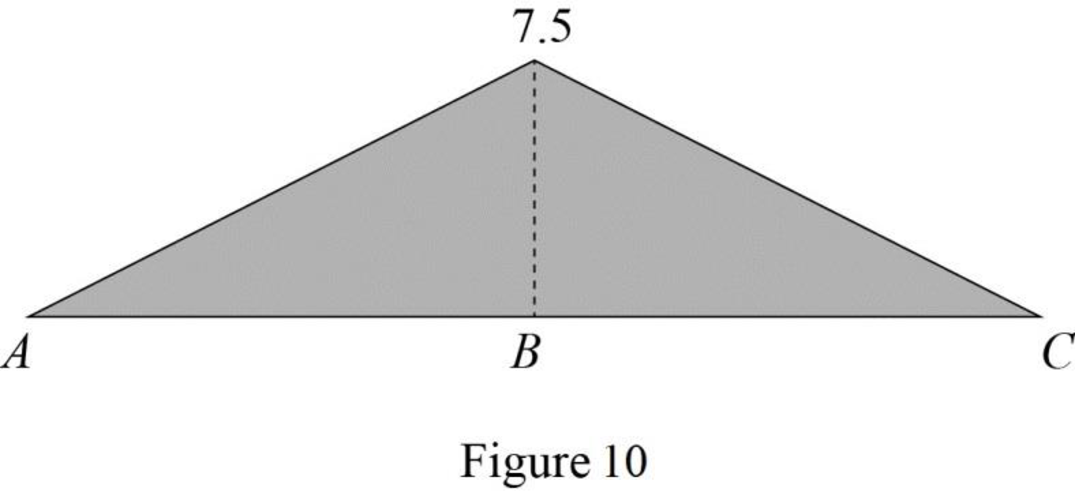
Refer Figure 9.
The slope of portion AB and BC is same.
Find the slope
Here,
Substitute 15 ft for
Find the maximum positive bending moment at B.
Refer Figure 6.
Find the bending moment at B when the load 1 placed at just right of B.
Substitute 15 ft for
Refer Figure 7.
Find the bending moment at B when the load 2 placed at just right of B.
Substitute 15 ft for
Refer Figure 8.
Find the bending moment at B when the load 3 placed at just right of B.
Substitute 15 ft for
Refer Figure 9.
Find the bending moment at B when the load 1 placed at just right of B.
Substitute 15 ft for
Maximum positive bending moment at B as follows.
The maximum positive bending moment at B is the maximum of
Therefore, the maximum positive bending moment at point B is
Want to see more full solutions like this?
Chapter 9 Solutions
Structural Analysis, SI Edition
- JOB UPDATE QUALCOMM FULL STACK DEVELOPER ASSOCIATE INFOR (FRESHERS) IBM QUALITY ENGINEER DATAVAIL DATABASE ADMINISTRATOR INTOUCH CUST SERVICE (CHAT/EMAIL) ACCENTURE Vinkjobs.com #vinkjobs CUSTOMER SUPPORT Search "Vinkjobs.com" on Googlearrow_forwardHello, I would like to ask if the answer provided in this link is correct based on the floor plan shown in the attached pictures? Kindly verify if the solution matches the actual layout and measurements. Thank you! https://www.bartleby.com/questions-and-answers/i-need-help-estimating-the-required-materials-for-masonry-works-using-chb-in-a-2-storey-residential-/bdb70948-ded3-4461-9057-f63a7a1c5f8farrow_forwardStructural analysis question Cleary explain each step with appropriate solviarrow_forward
- An activity on a non critical path has a total float of 16 days and a duration of 5 days. The start of the activity is delayed by delivery of material for 12 days. A worker shortage makes the activity take 12 days. How far behind the original critical path schedule are you? b.3 days a.0 days d.4 days c.4 days aheadarrow_forwardPlease answer the two questions in detail and as best as you can. Please ensure it is 100% done by human, please do not use AI or chatgpt.arrow_forwardPlease answer the two questions in detail and as best as you can. Please ensure it is 100% done by human, please do not use AI or chatgpt.arrow_forward
- Please answer the two questions in detail and as best as you can. Please ensure it is 100% done by human, please do not use AI or chatgpt.arrow_forwardPlease answer the two questions in detail and as best as you can. Please ensure it is 100% done by human, please do not use AI or chatgpt.arrow_forwardPlease answer the two questions in detail and as best as you can. Please ensure it is 100% done by human, please do not use AI or chatgpt.arrow_forward
- Please provide a handwritten solution to the questionarrow_forwardkevin.w.wickline@wv.govarrow_forwardWhat is the value of the influence line for the bending moment around B at B for the beam shown? Determine the influence line ordinates at 3-m intervals. Select the reaction at support C to be the redundant. A a. 1.875 kN 6 m b. 0.688 kN c. 2.25 kN > d. 0.313 KN B -12 m- El = constant Carrow_forward
