
Concept explainers
(a)
The point moves a greater distance in a given time, if the disk rotates with increasing
(a)
Answer to Problem 1P
The particle on the rim covers a greater linear distance as compared to the particle situated half way between the rim and the axis of rotation.
Explanation of Solution
Given:
A disk rotating with increasing angular velocity about an axis passing through its center and perpendicular to its plane.
Distance of the particle 1 (on the rim) from the axis of rotation
Distance of particle 2 (half way between the axis of rotation and the rim) from the axis of rotation
Here, the radius of the disk is
Formula used:
The
Here,
The angular acceleration of a point on the rotating disk is related to the linear acceleration
Here,
The linear distance
Calculations:
The disk of radius
from the axis of rotation. This is shown in the figure 1 below:
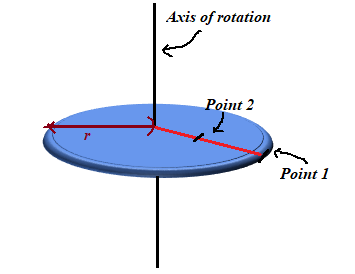
Figure 1
If the disk rotates with an angular acceleration
Calculate the linear accelerations of the particles located at point 1 and 2 using the equation (2).
Substitute
Therefore, from the above equations,
If the disk is assumed to start from rest, both particles would start with their initial velocities
Use equation (3) to calculate the distance travelled by the two points.
From equation (5),
Conclusion:
Therefore, the point on the rim travels a greater distance when compared to the point located halfway between the rim and the axis of rotation.
(b)
The point that turns through a greater angle.
(b)
Answer to Problem 1P
Both the points turn through the same angle.
Explanation of Solution
Formula used:
The
Here
Calculation:
The points 1 and 2 located at points A and B on the disc rotating with an angular acceleration
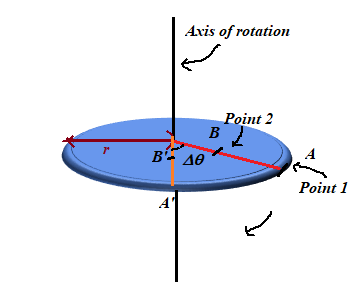
Figure 2
At any instant of time, both particles have the same instantaneous angular velocity and angular acceleration. As it can be seen from Figure 2, both particles describe the same angle at an instant of time.
Conclusion:
Thus, the particle located at the rim and the particle located half way between the rim and the axis of rotation turn through the same angle.
(c)
The point which travels with greater speed.
(c)
Answer to Problem 1P
The point on the rim travels with greater speed.
Explanation of Solution
Formula used:
The instantaneous speed
Here,
Calculation:
The disk moves with increasing angular velocity. But, both points at any instant would have the same instantaneous angular velocity, since they turn through the same angle in a given interval of time.
Hence, it can be inferred from equation (7):
Since the point on the rim has the greater value of
Conclusion:
Thus, the point on the rim would have a greater speed when compared to the point located half way between the rim and the axis of rotation.
(d)
The point which has the greater angular speed.
(d)
Answer to Problem 1P
Both the particles have the same angular speed.
Explanation of Solution
Formula used:
The angular velocity of a particle is given by
Calculation:
From Figure 2, it is seen that at any instant of time, both particles 1 and 2 cover the same angles. Hence, the rate of change of their angular displacement
Conclusion:
Thus, the particle on the rim and the particle located halfway between the rim and the axis of rotation have the same angular velocity.
(e)
The point which has the greater tangential acceleration.
(e)
Answer to Problem 1P
The point on the rim has a greater tangential acceleration when compared to the point located midway between the rim and the axis of rotation:
Explanation of Solution
Formula used:
The tangential acceleration
Calculation:
If the disk rotates with a varying angular velocity, it has angular acceleration. Assuming that the angular acceleration of the disk remains constant, from equation (9) it can be inferred that
The point on the rim has the greater value of
Therefore, the point on the rim has a greater tangential acceleration when compared to any point located inside the rim. This is also proved by the fact that the point on the rim gains a larger tangential velocity when compared to any inner point.
Conclusion:
Thus, the point on the rim has a greater tangential acceleration when compared to the point located midway between the rim and the axis of rotation.
(f)
The point which has a greater angular acceleration.
(f)
Answer to Problem 1P
Both particles have the same angular acceleration.
Explanation of Solution
Formula used:
The angular acceleration
Calculation:
It has been proved in (d) that at any instant of time, both the particles have the same angular velocity. Therefore, in an interval of time
Hence, from equation (1), it can be proved that at a given instant of time, both the points will have the same angular accelerations.
Conclusion:
Thus, both particles are found to have the same angular acceleration.
(g)
The point which has the greater centripetal acceleration.
(g)
Answer to Problem 1P
The point on the rim has a greater centripetal acceleration.
Explanation of Solution
Formula used:
The centripetal acceleration of a point located at a distance
Calculation:
It has been established in part (d) that at any instant of time, the point on the rim and the point located halfway between the rim and the axis of rotation have the same angular velocity.
Therefore, from equation (10), it can be inferred that
The point on the rim has the greater value of
Conclusion:
Thus, the point on the rim has a greater centripetal acceleration.
Want to see more full solutions like this?
Chapter 9 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- When 1.00 g of water at 100˚C changes from the liquid to the gas phase at atmospheric pressure, its change in volume is: 1.67 x 10^-3 How much heat is added to vaporize the water? How much work is done by the water against the atmosphere in expansion? What is the change in the internal energy of the water?arrow_forward1 m3 of pure water is heated from 10˚C to 120˚C at a constant pressure of 1 atm. The volume of the water is contained, but allowed to expand as needed remaining at 1 atm. Calculate the change in enthalpy of the water. You are provided with the following information at the conditions of 1 atm: The density of pure water between 10˚C and 100˚C: 1000kh/m^3 The heat capacity of water: 4.18 kj/kgK Enthalpy required to convert liquid water to gas (enthalpy of vaporization): 2260 kj/kg The heat capacity of steam: 1.7kj/kgk Is the reaction endothermic or exothermic? Why?arrow_forwardWhen a dilute gas expands quasi-statically from 0.50 to 4.0 L, it does 250 J of work. Assuming that the gas temperature remains constant at 300 K. What is the change in the internal energy of the gas? How much heat is absorbed by the gas in this process?arrow_forward
- A high-speed lifting mechanism supports an 881 kg object with a steel cable that is 22.0 m long and 4.00 cm^2 in cross-sectional area. Young's modulus for steel is 20.0 ⋅10^10 Pa. Determine the elongation of the cable.arrow_forwardNamor, from Wakanda Forever, sits on a throne at the bottom of the ocean in a city called Talocan (and Atlantis in the comics). Assuming he, including his gold headdress, has a density of 1085 kg/m3 and that Namor is surrounded by salt water with a density of 1027 kg/m3, what is Namor’s normal force while sitting underwater? Take Namor’s mass as 285. kg and solve as if he has a uniform density.arrow_forwardTo get there they need to travel through an area of salt-water, which seems to also be a magical portal, before arriving in a dry area. Judging by the time Maui and Moana spend falling through the water, it seems they dive 3440. ft deep. Assume the portal is non-magical salt-water, with a density of 1027 kg/m^3. Given that the air pressure above the portal is 1.013 ⋅10^5 Pa, what is the pressure when they are 3440. ft deep? 1 m = 3.28 ft. Moana would have a surface area of 1.30 m2. How much force would be acting on her at the bottom of this portal?arrow_forward
- A plank 2.00 cm thick and 15.7 cm wide is firmly attached to the railing of a ship by clamps so that the rest of the board extends 2.00 m horizontally over the sea below. A man of mass 92.9 kg is forced to stand on the very end. If the end of the board drops by 5.97 cm because of the man's weight, find the shear modulus of the wood.arrow_forwardwhen considering particle B (4,1) distances in relation to P (-4, 5), why are the y coordinates being used gto resolve the distance along the x-axis and vice-versa?arrow_forwardA 198 kg load is hung on a wire of length of 3.58 m, cross-sectional area 2.00⋅ 10-5 m2, and Young's modulus 8.00⋅10^10 Pa. What is its increase in length?arrow_forward
- I. Pushing on a File Cabinet Bob has been asked to push a heavy file cabinet down the hall to another office. It's not on rollers, so there is a lot of friction. At time t = 0 seconds, he starts pushing it from rest with increasing force until it starts to move at t = 2 seconds. He pushes the file cabinet down the hall with varying amounts of force. The velocity versus time graph of the cabinet is shown below. A. On the graphs provided below, 1. draw the net force vs. time that would produce this velocity graph; 2. draw the friction force vs. time for this motion; 3. draw the applied force (Fon Cabinet by Bob) VS. time for this motion (the first two seconds of this graph have been drawn for you). Velocity (m/s) Applied Force (N) Friction Force (N) Net Force (N) A -m B -U time (s) D time (s) time (s) time (s)arrow_forwardanswer itarrow_forwardPlease draw a sketch and a FBDarrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





