Chapter 9, Problem 1NT

NOW TRY THIS

a. In an experiment of tossing a fair die once, what is the sum of the probabilities of all the distinct outcomes in the sample space?

b. Does the sum of the probabilities of all the distinct outcomes of any sample space always result in same number?

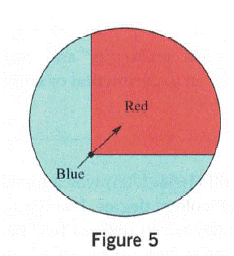
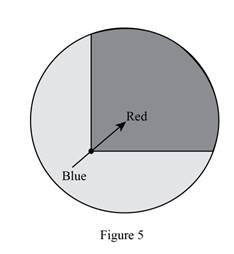
c. What is the probability of the spinner in Figure $5$ landing on Red? Why?

To determine

a.

To explain:

The sum of all the distinct outcomes in the sample space.

Answer to Problem 1NT

Solution:

The sum of probabilities of all the distinct outcomes in the sample space is always $1$.

Explanation of Solution

Given:

A fair die is tossed once.

Approach:

By calculating the probability for each event and taking the sum or by using the result that the sum of probabilities of all the events of sample space is $1$.

Calculation:

As on tossing a fair die sample space is $S=\left\{1,2,3,4,5,6\right\}$ and probability for each outcome is equal to $\frac{1}{6}$ and taking the sum gives $\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=1$.

To determine

b.

To explain:

Whether the sum of all the probabilities of all the distinct outcomes of any sample space always result in same number.

Answer to Problem 1NT

Solution:

Yes the sum of all the probabilities of all the distinct outcomes of any sample space always result in same number equal to $1$.

Explanation of Solution

Approach:

As the probability is the no. of times event happened divided by total events and when the sum is taken for all probabilities it gives $1$.

Calculation:

As on tossing a fair die sample space is $S=\left\{1,2,3,4,5,6\right\}$ and probability for each outcome is equal to $\frac{1}{6}$ and taking the sum gives $\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=1$.

To determine

c.

To explain:

The probability of spinner landing on Red.

Answer to Problem 1NT

Solution:

The probability of spinner landing on red is nearly $\frac{1}{3}$ as one third part of the circle is covered with Red color.

Explanation of Solution

Given:

A following spinner is given:

Approach:

By calculating the area covered by the color Red and taking the probability of it by whole area.

Calculation:

As the area of the Red part is nearly third part of the total area of the circle so the probability of getting red color on spinner is $\frac{1}{3}$.