
Concept explainers
NOW TRY THIS
a. In an experiment of tossing a fair die once, what is the sum of the probabilities of all the distinct outcomes in the
b. Does the sum of the probabilities of all the distinct outcomes of any sample space always result in same number?
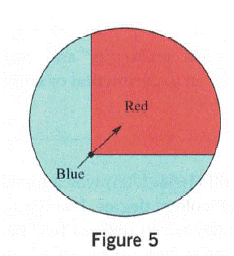
c. What is the probability of the spinner in Figure
a.
To explain:
The sum of all the distinct outcomes in the sample space.
Answer to Problem 1NT
Solution:
The sum of probabilities of all the distinct outcomes in the sample space is always
Explanation of Solution
Given:
A fair die is tossed once.
Approach:
By calculating the probability for each event and taking the sum or by using the result that the sum of probabilities of all the events of sample space is
Calculation:
As on tossing a fair die sample space is
b.
To explain:
Whether the sum of all the probabilities of all the distinct outcomes of any sample space always result in same number.
Answer to Problem 1NT
Solution:
Yes the sum of all the probabilities of all the distinct outcomes of any sample space always result in same number equal to
Explanation of Solution
Approach:
As the probability is the no. of times event happened divided by total events and when the sum is taken for all probabilities it gives
Calculation:
As on tossing a fair die sample space is
c.
To explain:
The probability of spinner landing on Red.
Answer to Problem 1NT
Solution:
The probability of spinner landing on red is nearly
Explanation of Solution
Given:
A following spinner is given:
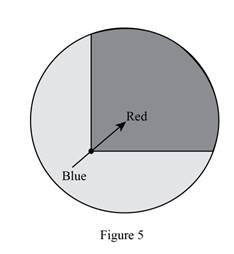
Approach:
By calculating the area covered by the color Red and taking the probability of it by whole area.
Calculation:
As the area of the Red part is nearly third part of the total area of the circle so the probability of getting red color on spinner is
Want to see more full solutions like this?
Chapter 9 Solutions
A Problem Solving Approach to Mathematics for Elementary School Teachers (12th Edition)
Additional Math Textbook Solutions
Pathways To Math Literacy (looseleaf)
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
Intermediate Algebra (13th Edition)
Introductory Statistics
Elementary Algebra For College Students (10th Edition)
- Consider the weighted voting system [11: 7, 4, 1]Find the Shapley-Shubik power distribution of this weighted voting system.List the power for each player as a fraction: P1: P2: P3:arrow_forwardConsider the weighted voting system [18: 15, 8, 3, 1]Find the Banzhaf power distribution of this weighted voting system.List the power for each player as a fraction: P1: P2: P3: P4:arrow_forwardConsider the weighted voting system [16: 15, 8, 3, 1]Find the Banzhaf power distribution of this weighted voting system.List the power for each player as a fraction: P1: P2: P3: P4:arrow_forward
- Consider the weighted voting system [18: 15, 8, 3, 1]Find the Banzhaf power distribution of this weighted voting system.List the power for each player as a fraction: P1 = P2 = P3 = P4 =arrow_forwardConsider the weighted voting system [18: 15, 8, 3, 1]Find the Banzhaf power distribution of this weighted voting system.List the power for each player as a fraction: P1: P2: P3: P4:arrow_forwardConsider the weighted voting system [18: 15, 8, 3, 1]Find the Banzhaf power distribution of this weighted voting system.List the power for each player as a fraction: P1: P2: P3: P4:arrow_forward
- Find the Banzhaf power distribution of the weighted voting system[26: 19, 15, 11, 6]Give each player's power as a fraction or decimal value P1 = P2 = P3 = P4 =arrow_forwardsolve it using augmented matrix. Also it is homeworkarrow_forward4. Now we'll look at a nonhomogeneous example. The general form for these is y' + p(x)y = f(x). For this problem, we will find solutions of the equation +2xy= xe (a) Identify p(x) and f(x) in the equation above. p(x) = f(x) = (b) The complementary equation is y' + p(x)y = 0. Write the complementary equation. (c) Find a solution for the complementary equation. We'll call this solution y₁. (You only need one particular solution, so you can let k = 0 here.) Y1 = (d) Check that y₁ satisfies the complementary equation, in other words, that y₁+ p(x)y₁ = 0.arrow_forward
- data managementarrow_forwarddata management 1arrow_forwardThe second solution I got is incorrect. What is the correct solution? The other thrree with checkmarks are correct Question 19 Score on last try: 0.75 of 1 pts. See Details for more. Get a similar question You can retry this question below Solve 3 sin 2 for the four smallest positive solutions 0.75/1 pt 81 99 Details T= 1.393,24.666,13.393,16.606 Give your answers accurate to at least two decimal places, as a list separated by commas Question Help: Message instructor Post to forum Submit Questionarrow_forward

 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning





