
Bucket A and block C are connected by a cable that passes over drum B. Knowing that drum B rotates slowly counterclockwise and that the coefficients of friction at all surfaces are μS = 0.35 and μk = 0.25, determine the smallest combined mass m of the bucket and its content for which block C will (a) remain at rest, (b) start moving up the incline, (c) continue moving up the incline at a constant speed.

Fig. P8.118
(a)
Find the smallest combined mass m of the bucket for the block C will remain at rest.
Answer to Problem 8.118P
The smallest combined mass m of the bucket is
Explanation of Solution
Given information:
The mass of the block C is
The coefficient of static friction is
The coefficient of kinetic friction is
Calculation:
Show the free-body diagram of the drum B as in Figure 1.
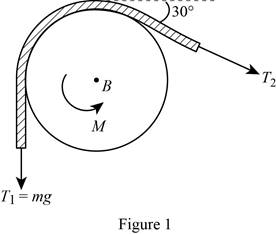
Find the angle of the belt wounded around the drum as follows;
Find the tension
Substitute mg for
Here, the acceleration due to gravity is g.
Consider the value of acceleration due to gravity is
Show the free-body diagram of the block C as in Figure 2.
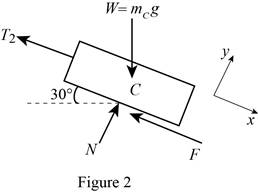
At rest, the cable slips on the drum. The motion impending is along the x-axis.
Substitute
Resolve the horizontal component of forces.
Substitute 100 kg for
Find the friction force (F) using the relation.
Substitute 0.35 for
Resolve the vertical component of forces.
Substitute
Therefore, the smallest combined mass m of the bucket is
(b)
Find the smallest combined mass m of the bucket for the block C start moving up the incline.
Answer to Problem 8.118P
The smallest combined mass m of the bucket is
Explanation of Solution
Given information:
The mass of the block C is
The coefficient of static friction is
The coefficient of kinetic friction is
Calculation:
Show the free-body diagram of the block C as in Figure 3.
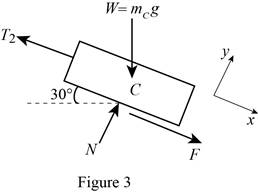
When the block start moving up the incline;
No slipping occurs at block and drum. The motion impending is against the x-axis.
Substitute
Resolve the horizontal component of forces.
Substitute 100 kg for
Find the friction force (F) using the relation.
Substitute 0.35 for
Resolve the vertical component of forces.
Substitute
Therefore, the smallest combined mass m of the bucket is
(c)
Find the smallest combined mass m of the bucket for the block C continue moving up the incline at constant speed.
Answer to Problem 8.118P
The smallest combined mass m of the bucket is
Explanation of Solution
Given information:
The mass of the block C is
The coefficient of static friction is
The coefficient of kinetic friction is
Calculation:
Show the free-body diagram of the block C as in Figure 3.
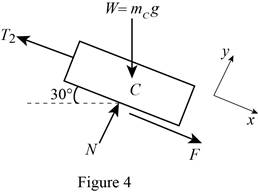
When the block start moving up the incline;
No slipping occurs at block and drum. The motion impending is against the x-axis.
Substitute
Resolve the horizontal component of forces.
Substitute 100 kg for
Find the friction force (F) using the relation.
Substitute 0.25 for
Resolve the vertical component of forces.
Substitute
Therefore, the smallest combined mass m of the bucket is
Want to see more full solutions like this?
Chapter 8 Solutions
VECTOR MECHANICS FOR ENGINEERS: STATICS
- Please can you help me with the attached question?arrow_forwardPlease can you help me with the attached question?arrow_forward4. The rod ABCD is made of an aluminum for which E = 70 GPa. For the loading shown, determine the deflection of (a) point B, (b) point D. 1.75 m Area = 800 mm² 100 kN B 1.25 m с Area = 500 mm² 75 kN 1.5 m D 50 kNarrow_forward
- Research and select different values for the R ratio from various engine models, then analyze how these changes affect instantaneous velocity and acceleration, presenting your findings visually using graphs.arrow_forwardQu. 7 The v -t graph of a car while travelling along a road is shown. Draw the s -t and a -t graphs for the motion. I need to draw a graph and I need to show all work step by step please do not get short cut from dtnaarrow_forwardAn unpressurized cylindrical tank with a 100-foot diameter holds a 40-foot column of water. What is total force acting against the bottom of the tank?arrow_forward
- 7. In the following problems check to see if the set S is a vector subspace of the corresponding R. If it is not, explain why not. If it is, then find a basis and the dimension. (a) S = (b) S = {[],+,"} X1 x12x2 = x3 CR³ {[1], 4+4 = 1} CR³ X2arrow_forwardAAA Show laplace transform on 1; (+) to L (y(+)) : SY(s) = x (0) Y(s) = £ [lx (+)] = 5 x(+) · est de 2 -St L [ y (^) ] = So KG) et de D 2 D D AA Y(A) → Y(s) Ŷ (+) → s Y(s) -yarrow_forward1) In each of the following scenarios, based on the plane of impact (shown with an (n, t)) and the motion of mass 1, draw the direction of motion of mass 2 after the impact. Note that in all scenarios, mass 2 is initially at rest. What can you say about the nature of the motion of mass 2 regardless of the scenario? m1 15 <+ m2 2) y "L χ m1 m2 m1 בז m2 Farrow_forward
- 8. In the following check to see if the set S is a vector subspace of the corresponding Rn. If it is not, explain why not. If it is, then find a basis and the dimension. X1 (a) S = X2 {[2], n ≤ n } c X1 X2 CR² X1 (b) S X2 = X3 X4 x1 + x2 x3 = 0arrow_forward2) Suppose that two unequal masses m₁ and m₂ are moving with initial velocities V₁ and V₂, respectively. The masses hit each other and have a coefficient of restitution e. After the impact, mass 1 and 2 head to their respective gaps at angles a and ẞ, respectively. Derive expressions for each of the angles in terms of the initial velocities and the coefficient of restitution. m1 m2 8 m1 ↑ บา m2 ñ Вarrow_forwardThe fallowing question is from a reeds book on applied heat i am studying. Although the answer is provided, im struggling to understand the whole answer and the formulas and the steps theyre using. Also where some ov the values such as Hg and Hf come from in part i for example. Please explain step per step in detail thanks In an NH, refrigerator, the ammonia leaves the evaporatorand enters the cornpressor as dry saturated vapour at 2.68 bar,it leaves the compressor and enters the condenser at 8.57 bar with50" of superheat. it is condensed at constant pressure and leavesthe condenser as saturated liquid. If the rate of flow of the refrigerantthrough the circuit is 0.45 kglmin calculate (i) the compressorpower, (ii) the heat rejected to the condenser cooling water in kJ/s,an (iii) the refrigerating effect in kJ/s. From tables page 12, NH,:2.68 bar, hg= 1430.58.57 bar, hf = 275.1 h supht 50" = 1597.2Mass flow of refrigerant--- - - 0.0075 kgls 60Enthalpy gain per kg of refrigerant in…arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





