
Concept explainers
Conversion of BCD (8421) numbers 11 0110 0101.0000 0111 to a decimal numbers.
Answer to Problem 21A
Decimal numbers is 365.0710.
Explanation of Solution
Given information:
A BCD (8421) numbers 11 0110 0101.0000 0111.
Calculation:
BCD number system uses 2 symbols: The numbers are 0 and 1.
And a decimal number system uses the number 10 as its base i.e. it has 10 symbols; decimal digits are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.
BCD numbers are represented as from decimal number
| BCD (8421) | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Each decimal digit consists of 4 BCD digits.
For example decimal number 9 is equal to BCD number 1001.
For converting integer part of BCD numbers into decimal numbers write down the BCD numbers and represent four binary digits from right by its decimal digit from the table.
Then combine all the digits together.
For converting fractional part of BCD numbers into decimal numbers write down the BCD numbers and represent four binary digits from left by its decimal digit from the table.
Then combine all the digits together.
Finally decimal number is combination of both integer and fractional part.
Decimal digits are equal to the summation of 2n where n = 0, 1, 2 and 3 (position from right)
For example 9 = 23+20; in this example 21 and 22 is not exist so at position 1 and 2 binary digit is zero and at position 0 and 3 binary digit is one; for example decimal of BCD 1001 is
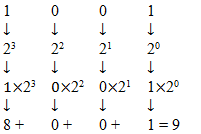
The decimal number is equal to the summation of binary digits dn × 2n
Divide the binary number into block of four digits if four digits are not exist the add additional zero in binary number for example 11 is written as 0011 and .11 is written as .1100
Decimal of BCD number 11 0110 0101.0000 0111 is (Starting from right for integer part and starting from left for fractional part)
Want to see more full solutions like this?
Chapter 84 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
- Complex Analysis 2 z3+3 Q1: Evaluate cz(z-i)² the Figure. First exam 2024-2025 dz, where C is the figure-eight contour shown inarrow_forwardConstruct a state-level description (i.e., a state diagram with transitions) for aTuring machine that decides the language {a^(n)b^(2n)c^(n) | n ∈ N}.arrow_forwardFind the sum of products expansion of the function F (x, y, z) = ̄x · y + x · z in two ways: (i) using a table; and (ii) using Boolean identitiesarrow_forward
- The NOR operator, denoted as ↓, behaves as 0 ↓ 0 = 1, 0 ↓ 1 = 0, 1 ↓ 0 = 0,1 ↓ 1 = 0. Show that the any Boolean function over any number of variables can be expressed using onlyNOR operators (in addition to those variables and constants). HINT: Recall that any Boolean function hasa representation as a sum of products expansionarrow_forwardConsider the Turing machine given in lecture which decides the languageB = {w#w | w is a binary string}.Simulate the Turing machine to show that the string 1001#1001 will be accepted by the Turing machine. Show all steps.arrow_forwardQ/Find the Laurent series of (2-3) cos↓ around z = 1. 2-1arrow_forward
- #1). A technique is given with 150 mAs is 40 kV and produces an EI value = 400. Find the new EI value, if mAs is 75 and 34 kV are used.arrow_forwardQ3: Answer the following: (i) Let f(z) is an analytic function in a simply connected domain S and y is a simple, closed, positively oriented contour lying in S. Prove that f, f(z)dz = 0.arrow_forwardUse the method of undetermined coefficients to solve the given nonhomogeneous system.X' = −1 33 −1 X + −4t2t + 2 X(t) =arrow_forward
- Detailed report without CHATGPT, accept if you can give with code and plots, previous reported . Do not waste my question.arrow_forwardPlease do not give inappropriate solutions, previous question reported, i need correct report solution for this, NO CHATGPTarrow_forwardNeed detailed report without CHATGPT, accept if you can give with code and plots, previous reported Plots are required.arrow_forward
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
 Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL




