Single Variable Calculus
8th Edition
ISBN: 9781305266636
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 8.3, Problem 7E
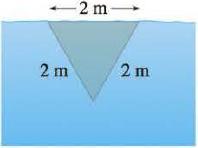
A vertical plate is submerged (or partially submerged) in water and has the indicated shape. Explain how to approximate the hydrostatic force against one side of the plate by a Riemann sum. Then express the force as an
7. 
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
An airplane flies due west at an airspeed of 428 mph. The wind blows in the direction of 41° south of west
at 50 mph. What is the ground speed of the airplane? What is the bearing of the airplane?
428 mph
41°
50 mph
a. The ground speed of the airplane is
b. The bearing of the airplane is
mph.
south of west.
Rylee's car is stuck in the mud. Roman and Shanice come along in a truck to help pull her out. They attach
one end of a tow strap to the front of the car and the other end to the truck's trailer hitch, and the truck
starts to pull. Meanwhile, Roman and Shanice get behind the car and push. The truck generates a
horizontal force of 377 lb on the car. Roman and Shanice are pushing at a slight upward angle and generate
a force of 119 lb on the car. These forces can be represented by vectors, as shown in the figure below. The
angle between these vectors is 20.2°. Find the resultant force (the vector sum), then give its magnitude
and its direction angle from the positive x-axis.
119 lb
20.2°
377 lb
a. The resultant force is
(Tip: omit degree notations from your answers; e.g. enter cos(45) instead of cos(45°))
b. It's magnitude is
lb.
c. It's angle from the positive x-axis is
Find a plane containing the point (3, -3, 1) and the line of intersection of the planes 2x + 3y - 3z = 14
and -3x - y + z = −21.
The equation of the plane is:
Chapter 8 Solutions
Single Variable Calculus
Ch. 8.1 - Use the arc length formula (3) to find the length...Ch. 8.1 - Use the arc length formula to find the length of...Ch. 8.1 - Set up an integral that represents the length of...Ch. 8.1 - Set up an integral that represents the length of...Ch. 8.1 - Set up an integral that represents the length of...Ch. 8.1 - Set up an integral that represents the length of...Ch. 8.1 - Set up an integral that represents the length of...Ch. 8.1 - Set up an integral that represents the length of...Ch. 8.1 - Find the exact length of the curve. 9. y = 1 +...Ch. 8.1 - Find the exact length of the curve. 10. 36y2 = (x2...
Ch. 8.1 - Find the exact length of the curve. 11....Ch. 8.1 - Find the exact length of the curve. 12....Ch. 8.1 - Find the exact length of the curve. 13....Ch. 8.1 - Find the exact length of the curve. 14. y = ln(cos...Ch. 8.1 - Find the exact length of the curve. 15. y = ln(sec...Ch. 8.1 - Find the exact length of the curve. 16....Ch. 8.1 - Find the exact length of the curve. 17....Ch. 8.1 - Find the exact length of the curve. 18....Ch. 8.1 - Find the exact length of the curve. 19....Ch. 8.1 - Find the exact length of the curve. 20. y = 1 ex,...Ch. 8.1 - Find the length of the arc of the curve from point...Ch. 8.1 - Find the length of the arc of the curve from point...Ch. 8.1 - Graph the curve and visually estimate its length....Ch. 8.1 - Prob. 24ECh. 8.1 - Prob. 25ECh. 8.1 - Prob. 26ECh. 8.1 - Prob. 27ECh. 8.1 - Prob. 28ECh. 8.1 - Prob. 29ECh. 8.1 - Prob. 30ECh. 8.1 - Prob. 33ECh. 8.1 - (a) Sketch the curve y3 = x2. (b) Use Formulas 3...Ch. 8.1 - Find the arc length function for the curve y =...Ch. 8.1 - (a) Find the arc length function for the curve y =...Ch. 8.1 - Find the arc length function for the curve...Ch. 8.1 - The arc length function for a curve y = f(x),...Ch. 8.1 - Prob. 39ECh. 8.1 - A steady wind blows a kite due west. The kites...Ch. 8.1 - A hawk flying at 15 m/s at an altitude of 180 m...Ch. 8.1 - Prob. 42ECh. 8.1 - Prob. 43ECh. 8.1 - (a) The figure shows a telephone wire hanging...Ch. 8.1 - Prob. 45ECh. 8.1 - The curves with equations x + y = l , n = 4, 6, 8,...Ch. 8.2 - (a) Set up an integral for the area of the surface...Ch. 8.2 - (a) Set up an integral for the area of the surface...Ch. 8.2 - (a) Set up an integral for the area of the surface...Ch. 8.2 - (a) Set up an integral for the area of the surface...Ch. 8.2 - (a) Set up an integral for the area of the surface...Ch. 8.2 - (a) Set up an integral for the area of the surface...Ch. 8.2 - Prob. 7ECh. 8.2 - Find the exact area of the surface obtained by...Ch. 8.2 - Prob. 9ECh. 8.2 - Find the exact area of the surface obtained by...Ch. 8.2 - Prob. 11ECh. 8.2 - Find the exact area of the surface obtained by...Ch. 8.2 - Prob. 13ECh. 8.2 - Prob. 14ECh. 8.2 - Prob. 15ECh. 8.2 - Prob. 16ECh. 8.2 - The given curve is rotated about the y-axis. Find...Ch. 8.2 - The given curve is rotated about the y-axis. Find...Ch. 8.2 - Prob. 19ECh. 8.2 - Prob. 20ECh. 8.2 - Prob. 21ECh. 8.2 - Prob. 22ECh. 8.2 - Prob. 23ECh. 8.2 - Prob. 24ECh. 8.2 - If the region R=(x,y)x1,0y1/x is rotated about the...Ch. 8.2 - If the infinite curve y = ex, x 0, is rotated...Ch. 8.2 - Prob. 29ECh. 8.2 - A group of engineers is building a parabolic...Ch. 8.2 - (a) The ellipsex2a2+y2b2=1abis rotated about the...Ch. 8.2 - Prob. 32ECh. 8.2 - If the curve y = f(x), a x b, is rotated about...Ch. 8.2 - Prob. 35ECh. 8.2 - Prob. 36ECh. 8.2 - Prob. 37ECh. 8.2 - Prob. 38ECh. 8.2 - Formula 4 is valid only when f(x) 0. Show that...Ch. 8.3 - An aquarium 5 ft long, 2 ft wide, and 3 ft deep is...Ch. 8.3 - A tank is 8 m long, 4 m wide, 2 m high, and...Ch. 8.3 - A vertical plate is submerged (or partially...Ch. 8.3 - A vertical plate is submerged (or partially...Ch. 8.3 - A vertical plate is submerged (or partially...Ch. 8.3 - A vertical plate is submerged (or partially...Ch. 8.3 - A vertical plate is submerged (or partially...Ch. 8.3 - A vertical plate is submerged (or partially...Ch. 8.3 - A vertical plate is submerged (or partially...Ch. 8.3 - A vertical plate is submerged (or partially...Ch. 8.3 - A vertical plate is submerged (or partially...Ch. 8.3 - A milk truck carries milk with density 64.6 lb/ft3...Ch. 8.3 - A trough is filled with a liquid of density 840...Ch. 8.3 - A vertical dam has a semicircular gate as shown in...Ch. 8.3 - Prob. 15ECh. 8.3 - Prob. 16ECh. 8.3 - A swimming pool is 20 ft wide and 40 ft long and...Ch. 8.3 - Prob. 18ECh. 8.3 - A metal plate was found submerged vertically in...Ch. 8.3 - Prob. 20ECh. 8.3 - Point-masses mi are located on the x-axis as...Ch. 8.3 - Point-masses mi are located on the x-axis as...Ch. 8.3 - The masses mi are located at the points Pi. Find...Ch. 8.3 - Prob. 24ECh. 8.3 - Sketch the region bounded by the curves, and...Ch. 8.3 - Prob. 26ECh. 8.3 - Prob. 27ECh. 8.3 - Sketch the region bounded by the curves, and...Ch. 8.3 - Prob. 29ECh. 8.3 - Prob. 30ECh. 8.3 - Find the centroid of the region bounded by the...Ch. 8.3 - Prob. 32ECh. 8.3 - Prob. 33ECh. 8.3 - Calculate the moments Mx and My and the center of...Ch. 8.3 - Calculate the moments Mx and My and the center of...Ch. 8.3 - Use Simpsons Rule to estimate the centroid of the...Ch. 8.3 - Find the centroid of the region bounded by the...Ch. 8.3 - Prob. 38ECh. 8.3 - Prove that the centroid of any triangle is located...Ch. 8.3 - Find the centroid of the region shown, not by...Ch. 8.3 - Find the centroid of the region shown, not by...Ch. 8.3 - Prob. 42ECh. 8.3 - Prob. 43ECh. 8.3 - Prob. 44ECh. 8.3 - Prob. 45ECh. 8.3 - Prob. 46ECh. 8.3 - Prob. 47ECh. 8.3 - The Second Theorem of Pappus is in the same spirit...Ch. 8.3 - Prob. 49ECh. 8.3 - Prob. 50ECh. 8.3 - Prob. 51ECh. 8.4 - The marginal cost function C(x) was defined to be...Ch. 8.4 - Prob. 2ECh. 8.4 - Prob. 3ECh. 8.4 - Prob. 4ECh. 8.4 - Prob. 5ECh. 8.4 - Prob. 6ECh. 8.4 - If a supply curve is modeled by the equation p =...Ch. 8.4 - In a purely competitive market, the price of a...Ch. 8.4 - Prob. 9ECh. 8.4 - A camera company estimates that the demand...Ch. 8.4 - Prob. 11ECh. 8.4 - A movie theater has been charging 10.00 per person...Ch. 8.4 - Prob. 13ECh. 8.4 - Prob. 14ECh. 8.4 - Prob. 15ECh. 8.4 - Prob. 16ECh. 8.4 - Prob. 17ECh. 8.4 - A hot, wet summer is causing a mosquito population...Ch. 8.4 - Prob. 19ECh. 8.4 - Prob. 20ECh. 8.4 - The dye dilution method is used to measure cardiac...Ch. 8.4 - Prob. 22ECh. 8.4 - The graph of the concentration function c(t) is...Ch. 8.5 - Let f (x) be the probability density function for...Ch. 8.5 - Let f(t) be the probability density function for...Ch. 8.5 - Prob. 3ECh. 8.5 - The density function f(x)=e3x(1+e3x)2 is an...Ch. 8.5 - Let f (x) = c/(1 + x2). (a) For what value of c is...Ch. 8.5 - Let f(x) = k (3x x2) if 0 x 3 and f(x) = 0 if x...Ch. 8.5 - Prob. 7ECh. 8.5 - (a) Explain why the function whose graph is shown...Ch. 8.5 - Show that the median waiting time for a phone call...Ch. 8.5 - (a) A type of light bulb is labeled as having an...Ch. 8.5 - Prob. 11ECh. 8.5 - The time between infection and the display of...Ch. 8.5 - REM sleep is the phase of sleep when most active...Ch. 8.5 - According to the National Health Survey, the...Ch. 8.5 - The Garbage Project at the University of Arizona...Ch. 8.5 - Boxes are labeled as containing 500 g of cereal....Ch. 8.5 - Prob. 17ECh. 8.5 - Prob. 18ECh. 8.5 - Prob. 19ECh. 8.5 - Prob. 20ECh. 8.5 - Prob. 21ECh. 8 - (a) How is the length of a curve defined? (b)...Ch. 8 - Prob. 2RCCCh. 8 - Prob. 3RCCCh. 8 - (a) What is the physical significance of the...Ch. 8 - Prob. 5RCCCh. 8 - Prob. 6RCCCh. 8 - Prob. 7RCCCh. 8 - Prob. 8RCCCh. 8 - Prob. 9RCCCh. 8 - Prob. 10RCCCh. 8 - Prob. 1RECh. 8 - Prob. 2RECh. 8 - Prob. 3RECh. 8 - Prob. 4RECh. 8 - Prob. 5RECh. 8 - Prob. 6RECh. 8 - Prob. 7RECh. 8 - Prob. 8RECh. 8 - Prob. 9RECh. 8 - Prob. 10RECh. 8 - A gate in an irrigation canal is constructed in...Ch. 8 - A trough is filled with water and its vertical...Ch. 8 - Find the centroid of the region shown. 13.Ch. 8 - Prob. 14RECh. 8 - Prob. 15RECh. 8 - Prob. 16RECh. 8 - Prob. 17RECh. 8 - Prob. 18RECh. 8 - Prob. 19RECh. 8 - After a 6-mg injection of dye into a heart, the...Ch. 8 - (a) Explain why the function...Ch. 8 - Lengths of human pregnancies are normally...Ch. 8 - The length of time spent waiting in line at a...Ch. 8 - Prob. 1PCh. 8 - Prob. 2PCh. 8 - If a sphere of radius r is sliced by a plane whose...Ch. 8 - (a) Show that an observer at height H above the...Ch. 8 - Prob. 5PCh. 8 - The figure shows a semicircle with radius 1,...Ch. 8 - Prob. 7PCh. 8 - Consider a flat metal plate to be placed...Ch. 8 - A uniform disk with radius 1 m is to be cut by a...Ch. 8 - Prob. 10PCh. 8 - In a famous 18th-century problem, known as Buffons...Ch. 8 - Prob. 12PCh. 8 - Prob. 13P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Determine whether the lines L₁ : F(t) = (−2, 3, −1)t + (0,2,-3) and L2 : ƒ(s) = (2, −3, 1)s + (−10, 17, -8) intersect. If they do, find the point of intersection. ● They intersect at the point They are skew lines They are parallel or equalarrow_forwardAnswer questions 2arrow_forwardHow does a fourier transform works?arrow_forward
- Determine the radius of convergence of a power series:12.6.5, 12.6.6, 12.6.7, 12.6.8Hint: Use Theorem12.5.1 and root test, ratio test, integral testarrow_forwardCan you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forwardCan you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forward
- There are three options for investing $1150. The first earns 10% compounded annually, the second earns 10% compounded quarterly, and the third earns 10% compounded continuously. Find equations that model each investment growth and use a graphing utility to graph each model in the same viewing window over a 20-year period. Use the graph to determine which investment yields the highest return after 20 years. What are the differences in earnings among the three investment? STEP 1: The formula for compound interest is A = nt = P(1 + − − ) n², where n is the number of compoundings per year, t is the number of years, r is the interest rate, P is the principal, and A is the amount (balance) after t years. For continuous compounding, the formula reduces to A = Pert Find r and n for each model, and use these values to write A in terms of t for each case. Annual Model r=0.10 A = Y(t) = 1150 (1.10)* n = 1 Quarterly Model r = 0.10 n = 4 A = Q(t) = 1150(1.025) 4t Continuous Model r=0.10 A = C(t) =…arrow_forwardUse a graphing utility to find the point of intersection, if any, of the graphs of the functions. Round your result to three decimal places. (Enter NONE in any unused answer blanks.) y = 100e0.01x (x, y) = y = 11,250 ×arrow_forward5. For the function y-x³-3x²-1, use derivatives to: (a) determine the intervals of increase and decrease. (b) determine the local (relative) maxima and minima. (e) determine the intervals of concavity. (d) determine the points of inflection. (e) sketch the graph with the above information indicated on the graph.arrow_forward
- Can you solve this 2 question numerical methodarrow_forward1. Estimate the area under the graph of f(x)-25-x from x=0 to x=5 using 5 approximating rectangles Using: (A) right endpoints. (B) left endpoints.arrow_forward9. Use fundamental theorem of calculus to find the derivative d a) *dt sin(x) b)(x)√1-2 dtarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
03a: Numerical Differentiation Review; Author: Jaisohn Kim;https://www.youtube.com/watch?v=IMYsqbV4CEg;License: Standard YouTube License, CC-BY