
Mouse in a Maze A mouse is placed in one of the compartments of the maze shown in Fig. 7. After each minute of looking unsuccessfully for food, the mouse exits through one of the doors at random and moves to an adjacent compartment. The Exit door is one way; that is, the mouse cannot return after it has exited the maze.
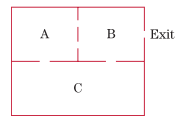
Figure 7
a. Draw the transition diagram for the Markov process.
b. Set up an absorbing stochastic matrix for the Markov process.
c. Find the stable matrix.
d. If the mouse begins in compartment A, what is the expected amount of time that it spends in the maze?
Note:
Want to see the full answer?
Check out a sample textbook solution
Chapter 8 Solutions
FINITE MATHEMATICS & ITS APPLICATIONS
- ANBNC ND B こ Ꭰarrow_forward1 Matching 10 points Factor and Solve 1)x3-216 0, x = {6,[B]} 2) 16x3 = 54 x-[3/2,[D]] 3)x4x2-42 0 x= [ +/-isqrt(7), [F] } 4)x+3-13-9x x=[+/-1.[H]] 5)x38x2+16x=0, x = {0,[K}} 6) 2x6-10x-48x2-0 x-[0, [M], +/-isqrt(3)) 7) 3x+2x²-8 x = {+/-i sqrt(2), {Q}} 8) 5x³-3x²+32x=2x+18 x = {3/5, [S]} [B] [D] [F] [H] [K] [M] [Q] +/-2 sqrt(2) +/- i sqrt(6) (-3+/-3 i sqrt(3))/4 +/- 1 +/-sqrt(6) +/- 2/3 sqrt(3) 4 -3 +/- 3 i sqrt(3) [S]arrow_forwardD U(AUBUC) B Darrow_forward
- helparrow_forwardAnswer question 2.28 please.arrow_forwardQuestion 2 Let F be a solenoidal vector field, suppose V × F = (-8xy + 12z², −9x² + 4y² + 9z², 6y²), and let (P,Q,R) = V²F(.725, —.283, 1.73). Then the value of sin(2P) + sin(3Q) + sin(4R) is -2.024 1.391 0.186 -0.994 -2.053 -0.647 -0.588 -1.851 1 ptsarrow_forward
- I just need b,c,darrow_forward1 pts Let F and G be vector fields such that ▼ × F(0, 0, 0) = (0.76, -9.78, 3.29), G(0, 0, 0) = (−3.99, 6.15, 2.94), and G is irrotational. Then sin(5V (F × G)) at (0, 0, 0) is Question 1 -0.246 0.072 -0.934 0.478 -0.914 -0.855 0.710 0.262 .arrow_forward8. In the following check to see if the set S is a vector subspace of the corresponding Rn. If it is not, explain why not. If it is, then find a basis and the dimension. X1 (a) S = X2 {[2], n ≤ n } c X1 X2 CR² X1 (b) S X2 = X3 X4 x1 + x2 x3 = 0arrow_forward
- Par quel quadrilatère est-elle représentée sur ce besoin en perspective cavalièrearrow_forwardPlease provide the solution for the attached image in detailed.arrow_forward5 Obtain by multiplying matrices the composite coordinate transformation of two transformations, first x' = (x + y√2+ z)/2 followed by y' = (x√√2-2√2)/2 z' = (-x+y√2-2)/2 x" = y" 2" = (x'√√2+2'√√2)/2 (-x'y'√√2+)/2 (x'y' √√2-z)/2.arrow_forward
 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning

