Single Variable Calculus: Early Transcendentals, Books a la Carte, and MyLab Math with Pearson eText -- Title-Specific Access Card Package (3rd Edition)

3rd Edition

ISBN: 9780134996103

Author: William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz

Publisher: PEARSON

See similar textbooks

Concept explainers

Optimization

Optimization comes from the same root as "optimal". "Optimal" means the highest. When you do the optimization process, that is when you are "making it best" to maximize everything and to achieve optimal results, a set of parameters is the base for the se…

Integration

Integration means to sum the things. In mathematics, it is the branch of Calculus which is used to find the area under the curve. The operation subtraction is the inverse of addition, division is the inverse of multiplication. In the same way, integratio…

Application of Integration

In mathematics, the process of integration is used to compute complex area related problems. With the application of integration, solving area related problems, whether they are a curve, or a curve between lines, can be done easily.

Volume

In mathematics, we describe the term volume as a quantity that can express the total space that an object occupies at any point in time. Usually, volumes can only be calculated for 3-dimensional objects. By 3-dimensional or 3D objects, we mean objects th…

Area

Area refers to the amount of space a figure encloses and the number of square units that cover a shape. It is two-dimensional and is measured in square units.

Videos

Textbook Question

Chapter 8.2, Problem 82E

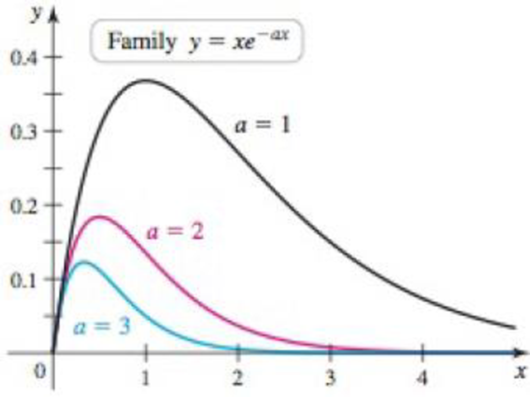
A family of exponentials The curves y = xe^−ax are shown in the figure for a = 1, 2, and 3.

a. Find the area of the region bounded by y = xe^−x and the x-axis on the interval [0, 4].
b. Find the area of the region bounded by y = xe^−ax and the x-axis on the interval [0, 4], where a > 0.
c. Find the area of the region bounded by y = xe^−ax and the x-axis on the interval [0, b]. Because this area depends on a and b, we call it A(a, b), where a > 0 and b > 0.
d. Use part (c) to show that A(l, ln b) = 4A(2, (ln b)/2).
e. Does this pattern continue? Is it true that A(1, ln b) = a²A(a, (ln b)/a)?

Chapter 8.2, Problem 82E, A family of exponentials The curves y = xeax are shown in the figure for a = 1, 2, and 3. a. Find

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 8.2, Problem 81E

Chapter 8.3, Problem 1QC

Students have asked these similar questions

Sketch a possible graph of a function f, together with vertical asymptotes, that satisfies all of the following conditions. f(2)=0 f(4) is undefined lim f(x)=1 X-6 lim f(x) = -∞ x-0+ lim f(x) = ∞ lim f(x) = ∞ x-4 _8

Determine the following limit. lim 35w² +8w+4 w→∞ √49w+w³ 3 Select the correct choice below, and, if necessary, fill in the answer box to complete your choice. ○ A. lim W→∞ 35w² +8w+4 49w+w3 (Simplify your answer.) B. The limit does not exist and is neither ∞ nor - ∞.

Calculate the limit lim X-a x-a 5 using the following factorization formula where n is a positive integer and x-➡a a is a real number. x-a = (x-a) (x1+x-2a+x lim x-a X - a x-a 5 = n- + xa an-2 + an−1)

Chapter 8 Solutions

Single Variable Calculus: Early Transcendentals, Books a la Carte, and MyLab Math with Pearson eText -- Title-Specific Access Card Package (3rd Edition)

Ch. 8.1 - What change of variable would you use for the...Ch. 8.1 - Prob. 2QC Ch. 8.1 - Prob. 3QC Ch. 8.1 - Prob. 4QC Ch. 8.1 - What change of variables would you use for the...Ch. 8.1 - Prob. 2E Ch. 8.1 - What trigonometric identity is useful in...Ch. 8.1 - Prob. 4E Ch. 8.1 - Prob. 5E Ch. 8.1 - Prob. 6E

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.