
Concept explainers
a)
Interpretation: Determine the order policy for the item based on silver-meal method.
Concept Introduction: Silver-Meal method is mainly used to determine the production quantities of the firm to be produced at the minimum cost.it is also provides the appropriate solutions to the time varying demand in production patterns.
a)
Answer to Problem 14P
The order policy according to silver meal method is 18 units in period-1,23 units in Period-4,50 units in Period-6,35 units in period-9 and 12 units in period-12.
Explanation of Solution
Given information: The anticipated demand for an inventory is as follows:
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Demand | 6 | 12 | 4 | 8 | 15 | 25 | 20 | 5 | 10 | 20 | 5 | 12 |
Current inventory is 4 and ending inventory is 8.
Holding cost (h) is $1 per period, set up cost (K) is $40
The objective of this method is to minimize the per-period-cost of ordering policy.
Net Requirements:
The order policy (lot-size) of the item under silver meal method can be calculated as follows:
According to silver meal method the average cost per period C (T) is a function of the average holding and set up cost per period for T number of Periods. The production in period 1 is equal to the demand in that period 1 to incur the order cost K.
Hence
And
And general equation is
Once
Now, calculate the order policy using the above formula as follows:
Starting in period 1:
Stop the process since
Starting in period 4:
Stop the process since
Starting in period 6:
Stop the process since
Starting in period 9:
Stop the process since
The same is explained with the help of a table shown below:
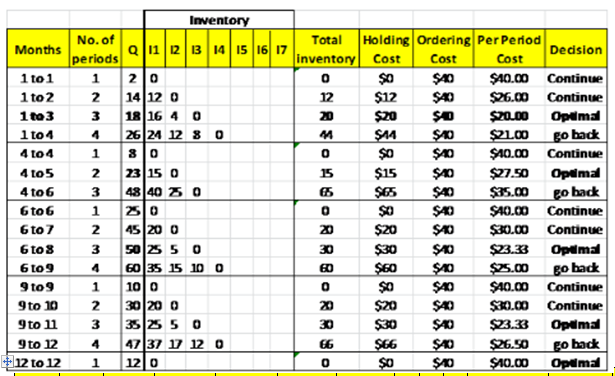
Table 1: Order Quantity using Silver-Meal Method:
| Months | No.of periods | Q | 11 | 12 | 13 | 14 | 15 | 16 | 17 | Total inventory | Holding Cost | Ordering Cost | Per Period Cost | Decision |
| 1 to 1 | 1 | 2 | 0 | =SUM(D3:J3) | =K3*1 | 40 | =SUM((L3:M3)/B3) | Continue | ||||||
| 1 to 2 | 2 | =2+12 | 12 | 0 | =SUM(D4:J4) | =K4*1 | 40 | =SUM((L4:M4)/B4) | Continue | |||||
| 1 to 3 | 3 | =14+4 | =C5-C3 | =C5-C4 | 0 | =SUM(D5:J5) | =K5*1 | 40 | =SUM((L5:M5)/B5) | Optimal | ||||
| 1 to 4 | 4 | =C5+8 | =C6-C3 | =C6-C4 | =C6-C5 | 0 | =SUM(D6:J6) | =K6*1 | 40 | =SUM((L6:M6)/B6) | Go Back | |||
| 4 to 4 | 1 | 8 | 0 | =SUM(D7:J7) | =K7*1 | 40 | =SUM((L7:M7)/B7) | Continue | ||||||
| 4 to 5 | 2 | =C7+15 | =C8-C7 | 0 | =SUM(D8:J8) | =K8*1 | 40 | =SUM((L8:M8)/B8) | Optimal | |||||
| 4 to 6 | 3 | =C8+25 | =C9-C7 | =C9-C8 | 0 | =SUM(D9:J9) | =K9*1 | 40 | =SUM((L9:M9)/B9) | Go Back | ||||
| 6 to 6 | 1 | 25 | 0 | =SUM(D10:J10) | =K10*1 | 40 | =SUM((L10:M10)/B10) | Continue | ||||||
| 6to 7 | 2 | =C10+20 | =C11-C10 | 0 | =SUM(D11:J11) | =K11*1 | 40 | =SUM((L11:M11)/B11) | Continue | |||||
| 6 to 8 | 3 | =C11+5 | =C12-C10 | =C12-C11 | 0 | =SUM(D12:J12) | =K12*1 | 40 | =SUM((L12:M12)/B12) | Optimal | ||||
| 6 to 9 | 4 | =C12+10 | =C13--C10 | =C13-C11 | =C13-C12 | =C13-C13 | =SUM(D13:J13) | =K13*1 | 40 | =SUM((L13:M13)/B13) | Go Back | |||
| 9 to 9 | 1 | 10 | 0 | =SUM(D14:J14) | =K14*1 | 40 | =SUM((L14:M14)/B14) | Continue | ||||||
| 9 to 10 | 2 | =C14+20 | =C15-C14 | 0 | =SUM(D15:J15) | =K15*1 | 40 | =SUM((L15:M15)/B15) | Continue | |||||
| 9 to 11 | 3 | =C15+5 | =C16-C14 | =C16-C15 | 0 | =SUM(D16:J16) | =K16*1 | 40 | =SUM((L16:M16)/B16) | Optimal | ||||
| 9 to 12 | 4 | =C16+12 | =C17--C14 | =C17-C15 | =C17-C16 | =C17-C17 | =SUM(D17:J17) | =K17*1 | 40 | =SUM((L17:M17)/B17) | Go Back | |||
| 12 to 12 | 1 | 12 | 0 | =SUM(D18:J18) | =K18*1 | 40 | =SUM((L18:M18)/B18) | Optimal |
b)
Interpretation: Determine the order policy for the item based on Least Unit Cost method.
Concept Introduction: Least unit cost produced the demand of the present periods based on the trial basis, yield the future periods. The method is calculated by adding the setup cost and carrying inventory cost and finally find the smallest cost per unit.
b)
Answer to Problem 14P
The order policy according to LUC method is 26 units in period-1, 40 units in Period-5, 25 units in Period-7, 35 units in period-9 and 12 units in period-12.
Explanation of Solution
Given information: The anticipated demand for a component VC is as follows:
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Demand | 42 | 42 | 32 | 12 | 26 | 112 | 45 | 14 | 76 | 38 |
Holding cost (h) is $0.60 per period, set up cost (K) is $132
The order policy (lot-size) of the item under Least Unit Cost(LUC)method can be calculated as follows:
LUC divides the average cost per period C (T) by the total number of units demanded. Hence
And
And general equation is
Once
Starting from period 1
Stop the process since
Starting in period 5:
Stop the process since
Starting in period 7:
Stop the process since
Starting in period 9:
Stop the process since
The same is explained with the help of a table shown below:
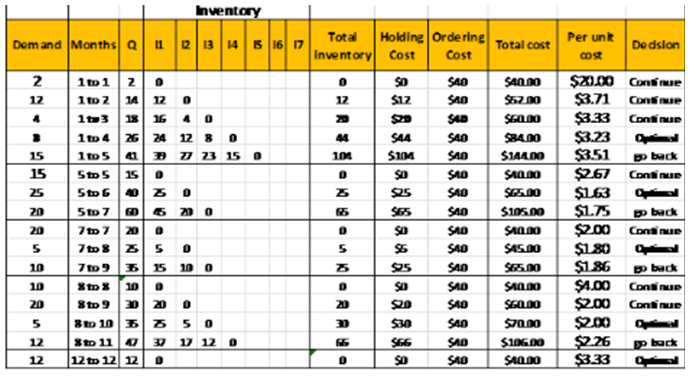
Table 2: Order Quantity using Least-Unit-Cost Method:
| Demand | Months | Q | 11 | 12 | 13 | 14 | 15 | Total inventory | Holding Cost | Ordering Cost | Total Cost | Per Period Cost | Decision |
| 2 | 1 to 1 | =A3 | 0 | =SUM(D3:H3) | =L3*1 | 40 | =K3+J3 | =L3/C3 | Continue | ||||
| 12 | 1 to 2 | =C3+A4 | =C4-C3 | 0 | =SUM(D4:H4) | =L4*1 | 40 | =K4+J4 | =L4/C4 | Continue | |||
| 4 | 1 to 3 | =C4+A5 | =C5-C3 | =C5-C4 | 0 | =SUM(D5:H5) | =L5*1 | 40 | =K5+J5 | =L5/C5 | Continue | ||
| 8 | 1 to 4 | =C5+A6 | =C6-C3 | =C6-C4 | =C6-C5 | =C6-C6 | =SUM(D6:H6) | =L6*1 | 40 | =K6+J6 | =L6/C6 | Optimal | |
| 15 | 1 to 5 | =C6+A7 | =C7-C3 | =C7-C4 | =C7-C5 | =C7-C6 | =C7-C7 | =SUM(D7:H7) | =L7*1 | =K7+J7 | =L7/C7 | Go Back | |
| 15 | 5 to 5 | =A8 | 0 | =SUM(D8:H8) | =L8*1 | 40 | =K8+J8 | =L8/C8 | Continue | ||||
| 25 | 5 to 6 | =C8+A9 | =C9-C8 | 0 | =SUM(D9:H9) | =L9*1 | 40 | =K9+J8 | =L9/C9 | Optimal | |||
| 20 | 5 to 7 | =C9+A11 | =C10-C8 | =C10-C9 | =C10-C10 | =SUM(D10:H10) | =L10*1 | 40 | =K10+J10 | =L10/C10 | Go Back | ||
| 20 | 7 to 7 | =A11 | 0 | =SUM(D11:H11) | =L11*1 | 40 | =K11+J11 | =L11/C11 | Continue | ||||
| 5 | 7 to 8 | =C11+A12 | =C12-C11 | 0 | =SUM(D12:H12) | =L12*1 | 40 | =K12+J12 | =L12/C12 | Optimal | |||
| 10 | 7 to 9 | =C12+A13 | =C13-C11 | =C13-C12 | =C13-C13 | =SUM(D13:H13) | =L13*1 | 40 | =K13+J13 | =L13/C13 | Go Back | ||
| 10 | 8 to 8 | =A14 | 0 | =SUM(D14:H14) | =L14*1 | 40 | =K14+J14 | =L14/C14 | Continue | ||||
| 20 | 8 to 9 | =C14+A15 | =C15-C14 | 0 | =SUM(D15:H15) | =L15*1 | 40 | =K15+J15 | =L15/C15 | Continue | |||
| 5 | 8 to 10 | =C15+A16 | =C16-C14 | =C16-C15 | 0 | =SUM(D16:H16) | =L16*1 | 40 | =K16+J16 | =L16/C16 | Optimal | ||
| 12 | 8 to 11 | =C16+A17 | =C17-C14 | =C17-C15 | -C17-C16 | =C17-C17 | =SUM(D17:H17) | =L17*1 | 40 | =K17+J17 | =L17/C17 | Go Back | |
| 12 | 12 to 12 | 12 | 0 | =SUM(D18:H18) | =L18*1 | 40 | =K18+J18 | ==L18/C18 | Optimal |
c)
Interpretation: Determine the order policy for the item based on Part Period Balancing method.
Concept Introduction: Part Period Balancing method is the lot-size method which use the starting and ending of the process function to consider the multiple periods to modifying the calculation based on the least total cost.
c)
Answer to Problem 14P
The order policy according to part period balancing method is 26 units in period-1, 60 units in Period-5, 35 units in Period-8, 17 units in period-11.
Explanation of Solution
Given information: The anticipated demand for a component VC is as follows:
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Demand | 42 | 42 | 32 | 12 | 26 | 112 | 45 | 14 | 76 | 38 |
Holding cost (h) is $0.60 per period, set up cost (K) is $132
The order policy (lot size) according to part period balancing method can be calculated as follows:
In this method the order horizon that equates holding and setup cost over that period has to be calculated as follows:
Starting from Period 1
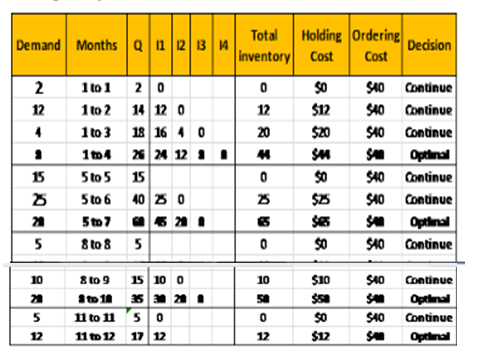
d)
Interpretation: Determine the three lot-sizing method resulted in the lowest cost for the 12 periods.
Concept Introduction: Lot size is determined the quantity order during the production time. The size of the lot may be dynamic or fixed.ERP (Enterprise Resource Planning) is the inbuilt multiple heuristic methods to determine the size of the lot to the production unit.
d)
Answer to Problem 14P
The Silver-meal method is giving lowest cost.
Explanation of Solution
Given information: The anticipated demand for a component VC is as follows:
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Demand | 42 | 42 | 32 | 12 | 26 | 112 | 45 | 14 | 76 | 38 |
Holding cost (h) is $0.60 per period, set up cost (K) is $132
Calculate the total cost of the ordering for the three methods as shown below:
| Silver-meal | Least Unit Cost | Part Period Balancing | |
| Holding Cost | =20+15+30+30 | =44+25+5+30 | =44+65+50+12 |
| Setup Cost | =40*5 | =40*5 | =4*40 |
| Total Cost | =B3+B2 | =C3+C2 | =D3+D2 |
| Silver-meal | Least Unit Cost | Part Period Balancing | |
| Holding Cost | 95 | 104 | 171 |
| Setup Cost | 200 | 200 | 160 |
| Total Cost | 295 | 304 | 331 |
Want to see more full solutions like this?
Chapter 8 Solutions
Production and Operations Analysis, Seventh Edition
- This area of emotional intelligence describes your ability to not only understand your strengths and weaknesses but to recognize your emotions and their effect on you and your team’s performance self management self awareness relationship management social awarenessarrow_forwardEmotional intelligence is defined as the ability to understand and manage your emotions, as well as recognize and influence the emotions of those around you. True Falsearrow_forwardAt the Ford automobile Highland plant, assume the one-millionth vehicle was produced in 1916 at a cost of $8084 (in 2013 US$), by how much did the Ford company reduce his cost with each doubling of cumulative output from 1916 to 1927?arrow_forward
- At the Ford automobile Highland plant,in 1913, how long did the average worker stay with the plant and what was the average tenure of a worker?arrow_forwardCommunity Federal Bank in Dothan, Alabama, recently increased its fees to customers who use employees as tellers. Management is interested in whether its new tee policy has increased the number of customers now using its automatic teller machines to that point that more machines are required. The following table provides the number of automatic teller transactions by week. Use trend projection with regression to forecast usage for weeks 13-16.arrow_forwardDavison Electronics manufactures three LED television monitors, identified as Model A, Model B, and Model C. Davison Electronics four manufacturing plants. Each model has its lowest possible production cost when produced at Plant 1. However, Plant 1 does not have the capacity to handle the total production of all three models. As a result, at least some of the production must be routed to the other manufacturing plants. The following table shows the minimum production requirements for next month, the plant capacities in units per month, and the production cost per unit at each plant: Model Production Cost per Unit Minimum Production Requirements Plant 1 Plant 2 Plant 3 Plant 4 A $25 $28 $37 $34 48,000 B $26 $35 $36 $41 75,000 C $20 $31 $26 $23 60,000 Production Capacity 65,000 50,000 32,000 43,000 Davison’s objective is to determine the cost-minimizing production planarrow_forward
- Anecdotally, entrepreneurs frequently encounter two critical dilemmas in managing human resources: the timing of hiring and the decision regarding hiring a generalist versus a specialist for their growing venture. Deciding when to expand a team is crucial, as premature hiring (i.e., hiring too soon) can strain resources, while delayed hiring (i.e., hiring too late) might hinder growth opportunities. Moreover, the choice between hiring a generalist or a specialist depends on the specific needs and stage of the venture, with each option presenting distinct advantages and challenges. To address these issues, a management scholar seeks to identify the factors shaping the hiring cycle throughout the entrepreneurial journey and to understand the criteria for choosing between generalists and specialists at various stages of a venture. The scholar has assembled a sample of 20 experienced South African entrepreneurs who have encountered both failure and success in the financial technology…arrow_forward3. [25 pts.] Four projects are available for investment. The projects require the cash flows and yield the net present values (NPV) (in millions) shown in the following table. Project id. 1 2 Cash outflow at time 0 (million Lira) 8 8 NPV (million Lira) 12 11 3 4 6 5 8 6 If 20 million Lira is available for investment at time 0, find the investment plan that maximizes NPV. All investments are required to be 0 or 1 (fractional investment values are not permitted). a. Formulate the mathematical model. (Write the decision variables, objective function and the constraints.) [10 pts.] b. Find the optimal solution by using Branch and Bound method (Draw the branch and bound tree clearly, write also lower bounds(LB)) (Left branches x=0, right branches x =1) [15 pts.].arrow_forwardexamine the production concept and operations management, what are the key steps required to achieve success? Be specific in your response.arrow_forward
- Produce a 3000 report with references on one international organization of your choice and Address the following: Provide a brief introduction of the organisation and sector it operates in, including its mission and vision statements, its core values, a summary of its financial performance and a general overview of the business’s operational activities. From the relevant literature explain the Total Quality Management (TQM) processes the chosen organization follows and identify one quality challenge/issue that the organization faced or is currently facing. Explain how the organization managed/or still managing the particular quality challenge/issue. Critically analyze whether the organization failed or succeeded in achieving and maintaining quality performance. Provide a few critical recommendations for business managers in order to highlight the importance of Total Quality Management (TQM) within an organization.arrow_forward問題2 Production system design involves determining the arrangement of workstations and the... O allocation of resources to workstations design of the process O production schedule all of the abovearrow_forwardElaborate on the need for and the benefits of an effective supply chain management (SCM) system in the context of a globalized and networked economy. In your answer, explain how organizations like Dell and Hewlett-Packard leverage supply chain networks to maintain competitiveness, and analyse the impact of globalization, technological advancements, and business environment changes on supply chain structures. Additionally, evaluate the key components of SCM, including distribution network configuration, inventory management, and cash-flow management, and discuss how these components contribute to creating an effective and integrated supply chain. (15) 3.2. Critically evaluate the requirements for effective inventory management within an organization. In your answer, discuss the importance of inventory accounting systems, the role of cost information (holding, ordering, and shortage costs), and the significance of classification systems like ABC analysis. Additionally, analyse how…arrow_forward
 Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning
Purchasing and Supply Chain ManagementOperations ManagementISBN:9781285869681Author:Robert M. Monczka, Robert B. Handfield, Larry C. Giunipero, James L. PattersonPublisher:Cengage Learning Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,- MarketingMarketingISBN:9780357033791Author:Pride, William MPublisher:South Western Educational Publishing



