Differential Equations: An Introduction to Modern Methods and Applications
Differential Equations: An Introduction to Modern Methods and Applications
3rd Edition
ISBN: 9781118531778
Author: James R. Brannan, William E. Boyce
Publisher: WILEY
bartleby

Concept explainers

Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
bartleby

Videos

Textbook Question
Book Icon
Chapter 8.2, Problem 13P

Complete the calculations leading to the entries in columns three and four of the table 8.2.1.

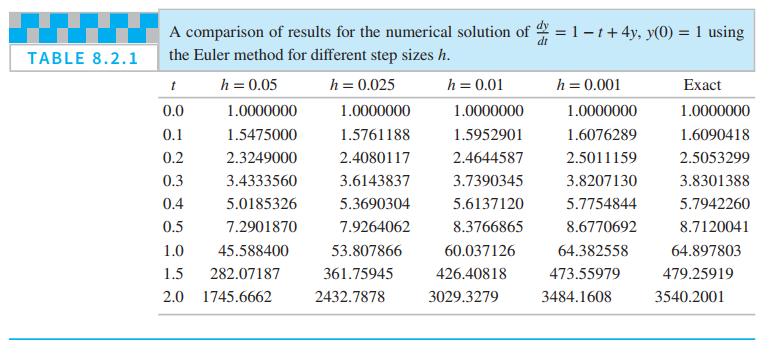
Chapter 8.2, Problem 13P, Complete the calculations leading to the entries in columns three and four of the table 8.2.1

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 8.2, Problem 12P
Next
Chapter 8.2, Problem 14P

Chapter 8 Solutions

Differential Equations: An Introduction to Modern Methods and Applications

Ch. 8.1 - In each of Problems 1 through 4 : Find approximate...Ch. 8.1 - In each of Problems 1 through 4 : Find approximate...Ch. 8.1 - In each of Problems 1 through 4: a) Find...Ch. 8.1 - In each of Problems 1 through 4 : Find approximate...Ch. 8.1 - In each of Problems 5 through 10 , draw a...Ch. 8.1 - In each of Problems 5 through 10, draw a direction...Ch. 8.1 - In each of Problems 5 through 10, draw a direction...Ch. 8.1 - In each of Problems 5 through 10, draw a direction...Ch. 8.1 - In each of Problems 5 through 10 , draw a...Ch. 8.1 - In each of Problems 5 through 10, draw a direction...
Ch. 8.1 - In each of Problems 11 through 14 , use Eular’s...Ch. 8.1 - In each of Problems 11 through 14 , use Eular’s...Ch. 8.1 - In each of Problems 11 through 14 , use Eular’s...Ch. 8.1 - In each of Problems 11 through 14 , use Eular’s...Ch. 8.1 - Consider the initial value problem...Ch. 8.1 - Consider the initial value problem Use Euler’s...Ch. 8.1 - Consider the initial value problem...Ch. 8.1 - Consider the initial value problem Where is a...Ch. 8.1 - Consider the initial value problem y=y2t2,y(0)=,...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - Complete the calculations leading to the entries...Ch. 8.2 - Using three terms in the Taylor series given in...Ch. 8.2 - In each of Problems 15 and 16, estimate the local...Ch. 8.2 - In each of Problems 15 and 16, estimate the local...Ch. 8.2 - In each of Problems 17 and 20, obtain a formula...Ch. 8.2 - In each of Problems 17 and 20, obtain a formula...Ch. 8.2 - In each of Problems 17 and 20, obtain a formula...Ch. 8.2 - In each of Problems 17 and 20, obtain a formula...Ch. 8.2 - Consider the initial value problem y=cos5t,y(0)=1....Ch. 8.2 - Using a step size h=0.05 and the Euler method,...Ch. 8.2 - The following problem illustrates a danger that...Ch. 8.2 - The distributive law a(bc)=abac does not hold, in...Ch. 8.2 - In this section we stated that the global...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - Complete the calculation leading to the entries in...Ch. 8.3 - Confirm the results in Table 8.3.2 by executing...Ch. 8.3 - Consider the initial value problem y=t2+y2,y(0)=1....Ch. 8.3 - Consider the initial value problem Draw a...Ch. 8.3 - In this problem, we establish that the local...Ch. 8.3 - Consider the improved Euler method for solving the...Ch. 8.3 - In each of Problems 19 and 20, use the actual...Ch. 8.3 - In each of Problems 19 and 20, use the actual...Ch. 8.3 - In each of Problems 21 through 24, carry out one...Ch. 8.3 - In each of Problems 21 through 24, carry out one...Ch. 8.3 - In each of Problems 21 through 24, carry out one...Ch. 8.3 - In each of Problems 21 through 24, carry out one...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - Consider the example problemwith the initial...Ch. 8.4 - Consider the initial value problem...Ch. 8.P1 - Assume that the shape of the dispensers are...Ch. 8.P1 - After viewing the results of her computer...Ch. 8.P2 - Show that Euler’s method applied to the...Ch. 8.P2 - Simulate five sample trajectories of Eq. (1) for...Ch. 8.P2 - Use the differential equation (4) to generate an...Ch. 8.P2 - Variance Reduction by Antithetic Variates. A...

Additional Math Textbook Solutions

Find more solutions based on key concepts
In the savings plan formula, assuming all other variables are constant, the accumulated balance in the savings ...

Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)

Highest Degree Planned The next table shows the results from The American Freshman: National Norms Fall 2015 of...

Finite Mathematics & Its Applications (12th Edition)

Challenge Yourself In Example 6, we found that the average daily balance method gave the highest finance charge...

Mathematics All Around (6th Edition)

If you multiply an odd number by 2 and add 1, is your answer even or odd?

A Problem Solving Approach to Mathematics for Elementary School Teachers (12th Edition)

Checkpoint1 Use the substitution method to solve this system: Answers to Checkpoint exercises are found at the...

Mathematics with Applications In the Management, Natural, and Social Sciences (12th Edition)

30. Web Data Sets. Go to any website that gives data sets, such as the Census Bureau, the U.S. Energy Informati...

Using & Understanding Mathematics: A Quantitative Reasoning Approach (7th Edition)

Knowledge Booster
Background pattern image
Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Text book image
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
SEE MORE TEXTBOOKS
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY