
MML PRECALCULUS ENHANCED
7th Edition
ISBN: 9780134119250
Author: Sullivan
Publisher: INTER PEAR
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 8.2, Problem 10SB
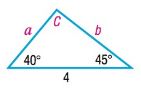
In Problems 9-16, solve each triangle.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(1) Write the following quadratic equation in terms of the vertex coordinates.
The final answer is 8/π(sinx) + 8/3π(sin 3x)+ 8/5π(sin5x)....
Keity
x२
1. (i)
Identify which of the following subsets of R2 are open and which
are not.
(a)
A = (2,4) x (1, 2),
(b)
B = (2,4) x {1,2},
(c)
C = (2,4) x R.
Provide a sketch and a brief explanation to each of your answers.
[6 Marks]
(ii)
Give an example of a bounded set in R2 which is not open.
[2 Marks]
(iii)
Give an example of an open set in R2 which is not bounded.
[2 Marks
Chapter 8 Solutions
MML PRECALCULUS ENHANCED
Ch. 8.1 - In a right triangle, if the length of the...Ch. 8.1 - If is an acute angle, solve the equation tan= 1 2...Ch. 8.1 - If is an acute angle, solve the equation sin= 1 2...Ch. 8.1 - True or False sin 52 =cos 48Ch. 8.1 - The sum of the measures of the two acute angles in...Ch. 8.1 - When you look up at an object, the acute angle...Ch. 8.1 - True or False In a right triangle, if two sides...Ch. 8.1 - True or False In a right triangle, if we know the...Ch. 8.1 - In Problems 9-18, find the exact value of the six...Ch. 8.1 - In Problems 9-18, find the exact value of the six...
Ch. 8.1 - In Problems 9-18, find the exact value of the six...Ch. 8.1 - In Problems 9-18, find the exact value of the six...Ch. 8.1 - In Problems 9-18, find the exact value of the six...Ch. 8.1 - In Problems 9-18, find the exact value of the six...Ch. 8.1 - In Problems 9-18, find the exact value of the six...Ch. 8.1 - Prob. 16SBCh. 8.1 - Prob. 17SBCh. 8.1 - In Problems 9-18, find the exact value of the six...Ch. 8.1 - Prob. 19SBCh. 8.1 - In Problems 19-28, find the exact value of each...Ch. 8.1 - Prob. 21SBCh. 8.1 - Prob. 22SBCh. 8.1 - In Problems 19-28, find the exact value of each...Ch. 8.1 - In Problems 19-28, find the exact value of each...Ch. 8.1 - In Problems 19-28, find the exact value of each...Ch. 8.1 - In Problems 19-28, find the exact value of each...Ch. 8.1 - In Problems 19-28, find the exact value of each...Ch. 8.1 - In Problems 19-28, find the exact value of each...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - In Problems 29-42, use the right triangle shown...Ch. 8.1 - Geometry The hypotenuse of a right triangle is 5...Ch. 8.1 - Geometry The hypotenuse of a right triangle is 3...Ch. 8.1 - Geometry A right triangle has a hypotenuse of...Ch. 8.1 - Geometry A right triangle has a hypotenuse of...Ch. 8.1 - Geometry A right triangle contains a 25 angle. (a)...Ch. 8.1 - Geometry A right triangle contains an angle of 8...Ch. 8.1 - Finding the Width of a Gorge Find the distance...Ch. 8.1 - Finding the Distance across a Pond Find the...Ch. 8.1 - The Eiffel Tower The tallest tower built before...Ch. 8.1 - Finding the Distance of a Ship from Shore A person...Ch. 8.1 - Finding the Distance to a Plateau Suppose that you...Ch. 8.1 - Finding the Reach of a Ladder A 22-foot extension...Ch. 8.1 - Finding the Angle of Elevation of the Sun At 10 AM...Ch. 8.1 - Directing a Laser Beam A laser beam is to be...Ch. 8.1 - Finding the Speed of a Truck A state trooper is...Ch. 8.1 - Security A security camera in a neighborhood bank...Ch. 8.1 - Parallax One method of measuring the distance from...Ch. 8.1 - Parallax See Problem 59. 61 Cygni, sometimes...Ch. 8.1 - Washington Monument The angle of elevation of the...Ch. 8.1 - Finding the Length of a Mountain Trail A straight...Ch. 8.1 - Finding the Bearing of an Aircraft A DC-9 aircraft...Ch. 8.1 - Prob. 64AECh. 8.1 - Niagara Falls Incline Railway Situated between...Ch. 8.1 - Willis Tower Willis Tower in Chicago is the second...Ch. 8.1 - Constructing a Highway A highway whose primary...Ch. 8.1 - Photography A camera is mounted on a tripod 4 feet...Ch. 8.1 - Finding the Distance between Two Objects A blimp,...Ch. 8.1 - Hot-Air Balloon While taking a ride in a hot-air...Ch. 8.1 - Mt. Rushmore To measure the height of Lincoln’s...Ch. 8.1 - The CN Tower The CN Tower, located in Toronto,...Ch. 8.1 - Chicago Skyscrapers The angle of inclination from...Ch. 8.1 - Estimating the Width of the Mississippi River A...Ch. 8.1 - Finding the Pitch of a Roof A carpenter is...Ch. 8.1 - Shooting Free Throws in Basketball The eyes of a...Ch. 8.1 - Geometry Find the value of the angle in degrees...Ch. 8.1 - Surveillance Satellites A surveillance satellite...Ch. 8.1 - Calculating Pool Shots A pool player located at X...Ch. 8.1 - One World Trade Center One World Trade Center...Ch. 8.1 - Explain how you would measure the width of the...Ch. 8.1 - Explain how you would measure the height of a TV...Ch. 8.1 - The Gibb’s Hill Lighthouse, Southampton, Bermuda...Ch. 8.1 - Determine whether x3 is a factor of x 4 +2 x 3 21...Ch. 8.1 - Find the exact value of sin15 . Hint: 15=4530Ch. 8.1 - Prob. 86RYKCh. 8.1 - Solve 2 sin 2 sin1=0 for 02 .Ch. 8.2 - The difference formula for the sine function is...Ch. 8.2 - If is an acute angle, solve the equation cos= 3 2...Ch. 8.2 - The two triangles shown are similar. Find the...Ch. 8.2 - If none of the angles of a triangle is a right...Ch. 8.2 - For a triangle with sides a, b, c and opposite...Ch. 8.2 - True or False An oblique triangle in which two...Ch. 8.2 - True or False The Law of Sines can be used to...Ch. 8.2 - Triangles for which two sides and the angle...Ch. 8.2 - In Problems 9-16, solve each triangle.Ch. 8.2 - In Problems 9-16, solve each triangle.Ch. 8.2 - In Problems 9-16, solve each triangle.Ch. 8.2 - In Problems 9-16, solve each triangle.Ch. 8.2 - In Problems 9-16, solve each triangle.Ch. 8.2 - In Problems 9-16, solve each triangle.Ch. 8.2 - In Problems 9-16, solve each triangle.Ch. 8.2 - In Problems 9-16, solve each triangle.Ch. 8.2 - In Problems 17-24, solve each triangle. A= 40 ,...Ch. 8.2 - In Problems 17-24, solve each triangle. A= 50 ,...Ch. 8.2 - In Problems 17-24, solve each triangle. B= 70 ,...Ch. 8.2 - In Problems 17-24, solve each triangle. A= 70 ,...Ch. 8.2 - In Problems 17-24, solve each triangle. A= 110 ,...Ch. 8.2 - In Problems 17-24, solve each triangle. B= 10 ,...Ch. 8.2 - In Problems 17-24, solve each triangle. A= 40 ,...Ch. 8.2 - In Problems 17-24, solve each triangle. B= 20 ,...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - In Problems 25-36, two sides and an angle are...Ch. 8.2 - Finding the Length of a Ski Lift Consult the...Ch. 8.2 - Finding the Height of a Mountain Use the...Ch. 8.2 - Finding the Height of an Airplane An aircraft is...Ch. 8.2 - Finding the Height of the Bridge over the Royal...Ch. 8.2 - Land Dimensions A triangular plot of land has one...Ch. 8.2 - Distance between Runners Two runners in a marathon...Ch. 8.2 - Landscaping Pat needs to determine the height of a...Ch. 8.2 - Construction A loading ramp 10 feet long that...Ch. 8.2 - Prob. 45AECh. 8.2 - Prob. 46AECh. 8.2 - Rescue at Sea Coast Guard Station Able is located...Ch. 8.2 - Prob. 48AECh. 8.2 - Finding the Lean of the Leaning Tower of Pisa The...Ch. 8.2 - Crankshafts on Cars On a certain automobile, the...Ch. 8.2 - Constructing a Highway A highway whose primary...Ch. 8.2 - Calculating Distances at Sea The navigator of a...Ch. 8.2 - Designing an Awning An awning that covers a...Ch. 8.2 - Finding Distances A forest ranger is walking on a...Ch. 8.2 - Prob. 55AECh. 8.2 - Determining the Height of an Aircraft Two sensors...Ch. 8.2 - The Original Ferris Wheel George Washington Gale...Ch. 8.2 - Mollweides Formula For any triangle, Mollweides...Ch. 8.2 - Mollweides Formula Another form of Mollweides...Ch. 8.2 - For any triangle, derive the formula a=bcosC+ccosB...Ch. 8.2 - Law of Tangents For any triangle, derive the Law...Ch. 8.2 - Prob. 64AECh. 8.2 - Make up three problems involving oblique...Ch. 8.2 - What do you do first if you are asked to solve a...Ch. 8.2 - What do you do first if you are asked to solve a...Ch. 8.2 - Solve Example 6 using right-triangle geometry....Ch. 8.2 - Solve: 3 x 3 +4 x 2 27x36=0Ch. 8.2 - Find the exact distance between P 1 =( 1,7 ) and P...Ch. 8.2 - Find the exact value of tan[ cos 1 ( 7 8 ) ] .Ch. 8.2 - Graph y=4sin( 1 2 x ) . Show at least two periods.Ch. 8.3 - Write the formula for the distance d from P 1 =( x...Ch. 8.3 - If is an acute angle, solve the equation cos= 2 2...Ch. 8.3 - If three sides of a triangle are given, the Law of...Ch. 8.3 - If one side and two angles of a triangle are...Ch. 8.3 - If two sides and the included angle of a triangle...Ch. 8.3 - True or False Given only the three sides of a...Ch. 8.3 - True or False The Law of Cosines states that the...Ch. 8.3 - True or False A special case of the Law of Cosines...Ch. 8.3 - In Problems 9-16, solve each triangle.Ch. 8.3 - In Problems 9-16, solve each triangle.Ch. 8.3 - In Problems 9-16, solve each triangle.Ch. 8.3 - In Problems 9-16, solve each triangle.Ch. 8.3 - In Problems 9-16, solve each triangle.Ch. 8.3 - In Problems 9-16, solve each triangle.Ch. 8.3 - In Problems 9-16, solve each triangle.Ch. 8.3 - In Problems 9-16, solve each triangle.Ch. 8.3 - In Problems 17-32, solve each triangle. a=3 , b=4...Ch. 8.3 - In Problems 17-32, solve each triangle. a=2 , c=1...Ch. 8.3 - In Problems 17-32, solve each triangle. b=1 , c=3...Ch. 8.3 - In Problems 17-32, solve each triangle. a=6 , b=4...Ch. 8.3 - In Problems 17-32, solve each triangle. a=3 , c=2...Ch. 8.3 - In Problems 17-32, solve each triangle. b=4 , c=1...Ch. 8.3 - In Problems 17-32, solve each triangle. a=2 , b=2...Ch. 8.3 - In Problems 17-32, solve each triangle. a=3 , c=2...Ch. 8.3 - In Problems 17-32, solve each triangle. a=12 ,...Ch. 8.3 - In Problems 17-32, solve each triangle. a=4 , b=5...Ch. 8.3 - In Problems 17-32, solve each triangle. a=2 , b=2...Ch. 8.3 - In Problems 17-32, solve each triangle. a=3 , b=3...Ch. 8.3 - In Problems 17-32, solve each triangle. a=5 , b=8...Ch. 8.3 - In Problems 17-32, solve each triangle. a=4 , b=3...Ch. 8.3 - In Problems 17-32, solve each triangle. a=10 , b=8...Ch. 8.3 - In Problems 17-32, solve each triangle. a=9 , b=7...Ch. 8.3 - In Problems 33-42, solve each triangle using...Ch. 8.3 - In Problems 33-42, solve each triangle using...Ch. 8.3 - In Problems 33-42, solve each triangle using...Ch. 8.3 - In Problems 33-42, solve each triangle using...Ch. 8.3 - In Problems 33-42, solve each triangle using...Ch. 8.3 - In Problems 33-42, solve each triangle using...Ch. 8.3 - In Problems 33-42, solve each triangle using...Ch. 8.3 - In Problems 33-42, solve each triangle using...Ch. 8.3 - In Problems 33-42, solve each triangle using...Ch. 8.3 - In Problems 33-42, solve each triangle using...Ch. 8.3 - Distance to the Green A golfer hits an errant tee...Ch. 8.3 - Navigation An airplane flies due north from Ft....Ch. 8.3 - Avoiding a Tropical Storm A cruise ship maintains...Ch. 8.3 - Revising a Flight Plan In attempting to fly from...Ch. 8.3 - Major League Baseball Field A major league...Ch. 8.3 - Little League Baseball Field According to Little...Ch. 8.3 - Finding the Length of a Guy Wire The height of a...Ch. 8.3 - Finding the Length of a Guy Wire A radio tower 500...Ch. 8.3 - Identifying Remains The Purkait triangle, located...Ch. 8.3 - Identifying Remains Like the Purkait triangle in...Ch. 8.3 - Soccer Angles A soccer goal is 8 yards wide....Ch. 8.3 - Wrigley Field, Home of the Chicago Cubs The...Ch. 8.3 - Little League Baseball The distance from home...Ch. 8.3 - Building a Swing Set Clint is building a wooden...Ch. 8.3 - Rods and Pistons Rod OA rotates about the fixed...Ch. 8.3 - Geometry Show that the length d of a chord of a...Ch. 8.3 - Prob. 60AECh. 8.3 - For any triangle, show that sin c 2 = ( sa )( sb )...Ch. 8.3 - Use the law of Cosines to prove the identity cosA...Ch. 8.3 - What do you do first if you are asked to solve a...Ch. 8.3 - What do you do first if you are asked to solve a...Ch. 8.3 - Make up an applied problem that requires using the...Ch. 8.3 - Write down your strategy for solving an oblique...Ch. 8.3 - State the Law of Cosines in words.Ch. 8.3 - Graph: R( x )= 2x+1 x3Ch. 8.3 - Solve 4 x =3 x+1 . If the solution is irrational,...Ch. 8.3 - Given tan= 2 6 5 and cos= 5 7 , find the exact...Ch. 8.3 - Find an equation for the graph.Ch. 8.4 - The area K of a triangle whose base is b and whose...Ch. 8.4 - If two sides a and b and the included angle C are...Ch. 8.4 - The area K of a triangle with sides a , b , and c...Ch. 8.4 - True or False The area of a triangle equals...Ch. 8.4 - Given two sides of a triangle, b and c , and the...Ch. 8.4 - Heron's Formula is used to find the area of...Ch. 8.4 - Prob. 7SBCh. 8.4 - Prob. 8SBCh. 8.4 - Prob. 9SBCh. 8.4 - Prob. 10SBCh. 8.4 - Prob. 11SBCh. 8.4 - Prob. 12SBCh. 8.4 - Prob. 13SBCh. 8.4 - Prob. 14SBCh. 8.4 - Prob. 15SBCh. 8.4 - Prob. 16SBCh. 8.4 - Prob. 17SBCh. 8.4 - Prob. 18SBCh. 8.4 - Prob. 19SBCh. 8.4 - Prob. 20SBCh. 8.4 - Prob. 21SBCh. 8.4 - Prob. 22SBCh. 8.4 - In Problems 15-26, find the area of each triangle....Ch. 8.4 - Prob. 24SBCh. 8.4 - Prob. 25SBCh. 8.4 - In Problems 15-26, find the area of each triangle....Ch. 8.4 - Area of an ASA Triangle If two angles and the...Ch. 8.4 - Area of a Triangle Prove the two other forms of...Ch. 8.4 - In Problems 29-34, use the results of Problem 27...Ch. 8.4 - In Problems 29-34, use the results of Problem 27...Ch. 8.4 - In Problems 29-34, use the results of Problem 27...Ch. 8.4 - In Problems 29-34, use the results of Problem 27...Ch. 8.4 - In Problems 29-34, use the results of Problem 27...Ch. 8.4 - In Problems 29-34, use the results of Problem 27...Ch. 8.4 - Area of a Segment Find the area of the segment...Ch. 8.4 - Area of a Segment Find the area of the segment of...Ch. 8.4 - Cost of a Triangular Lot The dimensions of a...Ch. 8.4 - Amount of Material to Make a Tent A cone-shaped...Ch. 8.4 - Prob. 39AECh. 8.4 - Dimensions of Home Plate The dimensions of home...Ch. 8.4 - Computing Areas See the figure. Find the area of...Ch. 8.4 - Geometry See the figure, which shows a circle of...Ch. 8.4 - Approximating the Area of a Lake To approximate...Ch. 8.4 - Bermuda Triangle The Bermuda Triangle is roughly...Ch. 8.4 - The Flatiron Building Completed in 1902 in New...Ch. 8.4 - Area of a Quadrilateral Bretschneider’s Formula...Ch. 8.4 - The Cow Problem A cow is tethered to one corner of...Ch. 8.4 - Perfect Triangles A perfect triangle is one having...Ch. 8.4 - If h 1 , h 2 , and h 3 are the altitudes dropped...Ch. 8.4 - Show that a formula for the altitude h from a...Ch. 8.4 - Inscribed Circle For Problems 55-58, the lines...Ch. 8.4 - Inscribed Circle For Problems 55-58, the lines...Ch. 8.4 - Inscribed Circle For Problems 55-58, the lines...Ch. 8.4 - Inscribed Circle For Problems 55-58, the lines...Ch. 8.4 - A triangle has vertices A( 0,0 ) , B( 1,0 ) , and...Ch. 8.4 - What do you do first if you are asked to find the...Ch. 8.4 - What do you do first if you are asked to find the...Ch. 8.4 - State the area of an SAS triangle in words.Ch. 8.4 - Without graphing, determine whether the quadratic...Ch. 8.4 - Solve the inequality: x+1 x 2 9 0Ch. 8.4 - P=( 7 3 , 2 3 ) is the point on the unit circle...Ch. 8.4 - Establish the identity: cscsin=coscotCh. 8.5 - The amplitude A and period T of f( x )=5sin( 4x )...Ch. 8.5 - The motion of an object obeys the equation d=4cos(...Ch. 8.5 - When a mass hanging from a spring is pulled down...Ch. 8.5 - True or False If the distance d of an object from...Ch. 8.5 - In Problems 5-8, an object attached to a coiled...Ch. 8.5 - In Problems 5-8, an object attached to a coiled...Ch. 8.5 - In Problems 5-8, an object attached to a coiled...Ch. 8.5 - In Problems 5-8, an object attached to a coiled...Ch. 8.5 - Rework Problem 5 under the same conditions, except...Ch. 8.5 - Rework Problem 6 under the same conditions, except...Ch. 8.5 - Rework Problem 7 under the same conditions, except...Ch. 8.5 - Rework Problem 8 under the same conditions, except...Ch. 8.5 - In Problems 13-20, the displacement d (in meters)...Ch. 8.5 - In Problems 13-20, the displacement d (in meters)...Ch. 8.5 - In Problems 13-20, the displacement d (in meters)...Ch. 8.5 - In Problems 13-20, the displacement d (in meters)...Ch. 8.5 - In Problems 13-20, the displacement d (in meters)...Ch. 8.5 - In Problems 13-20, the displacement d (in meters)...Ch. 8.5 - In Problems 13-20, the displacement d (in meters)...Ch. 8.5 - In Problems 13-20, the displacement d (in meters)...Ch. 8.5 - In Problems 21-24, graph each damped vibration...Ch. 8.5 - In Problems 21-24, graph each damped vibration...Ch. 8.5 - In Problems 21-24, graph each damped vibration...Ch. 8.5 - In Problems 21-24, graph each damped vibration...Ch. 8.5 - In Problems 25-32, use the method of adding...Ch. 8.5 - In Problems 25-32, use the method of adding...Ch. 8.5 - In Problems 25-32, use the method of adding...Ch. 8.5 - In Problems 25-32, use the method of adding...Ch. 8.5 - In Problems 25-32, use the method of adding...Ch. 8.5 - In Problems 25-32, use the method of adding...Ch. 8.5 - In Problems 25-32, use the method of adding...Ch. 8.5 - In Problems 25-32, use the method of adding...Ch. 8.5 - In Problems 33-38, (a) use the Product-to-Sum...Ch. 8.5 - In Problems 33-38, (a) use the Product-to-Sum...Ch. 8.5 - In Problems 33-38, (a) use the Product-to-Sum...Ch. 8.5 - In Problems 33-38, (a) use the Product-to-Sum...Ch. 8.5 - In Problems 33-38, (a) use the Product-to-Sum...Ch. 8.5 - In Problems 3338, (a) use the ProducttoSum...Ch. 8.5 - In Problems 39-44, an object of mass m (in grams)...Ch. 8.5 - In Problems 39-44, an object of mass m (in grams)...Ch. 8.5 - In Problems 39-44, an object of mass m (in grams)...Ch. 8.5 - In Problems 39-44, an object of mass m (in grams)...Ch. 8.5 - In Problems 39-44, an object of mass m (in grams)...Ch. 8.5 - In Problems 39-44, an object of mass m (in grams)...Ch. 8.5 - In Problems 45-50. the distance d (in meters) of...Ch. 8.5 - In Problems 45-50. the distance d (in meters) of...Ch. 8.5 - In Problems 45-50. the distance d (in meters) of...Ch. 8.5 - In Problems 45-50. the distance d (in meters) of...Ch. 8.5 - In Problems 45-50. the distance d (in meters) of...Ch. 8.5 - In Problems 45-50. the distance d (in meters) of...Ch. 8.5 - Loudspeaker A loudspeaker diaphragm is oscillating...Ch. 8.5 - Colossus Added to Six Flags St. Louis in 1986, the...Ch. 8.5 - Tuning Fork The end of a tuning fork moves in...Ch. 8.5 - Tuning Fork The end of a tuning fork moves in...Ch. 8.5 - Charging a Capacitor See the illustration. If a...Ch. 8.5 - The Sawtooth Curve An oscilloscope often displays...Ch. 8.5 - Touch-Tone Phones On a Touch-Tone phone, each...Ch. 8.5 - Use a graphing utility to graph the sound emitted...Ch. 8.5 - Use a graphing utility to graph the function f( x...Ch. 8.5 - Use a graphing utility to graph y=xsinx,y= x 2...Ch. 8.5 - Use a graphing utility to graph y= 1 x sinx,y= 1 x...Ch. 8.5 - How would you explain to a friend what simple...Ch. 8.5 - Problems 65-68 are based on material learned...Ch. 8.5 - Problems 65-68 are based on material learned...Ch. 8.5 - Problems 65-68 are based on material learned...Ch. 8.R - In Problems 1 and 2, find the exact value of the...Ch. 8.R - In Problems 1 and 2, find the exact value of the...Ch. 8.R - In Problems 3-5, find the exact value of each...Ch. 8.R - In Problems 3-5, find the exact value of each...Ch. 8.R - In Problems 3-5, find the exact value of each...Ch. 8.R - In Problems 6 and 7, solve each triangle.Ch. 8.R - In Problems 6 and 7, solve each triangle.Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 8-20, find the remaining angle(s) and...Ch. 8.R - In Problems 21-25, find the area of each triangle....Ch. 8.R - In Problems 21-25, find the area of each triangle....Ch. 8.R - In Problems 21-25, find the area of each triangle....Ch. 8.R - In Problems 21-25, find the area of each triangle....Ch. 8.R - In Problems 21-25, find the area of each triangle....Ch. 8.R - Area of a Segment Find the area of the segment of...Ch. 8.R - Geometry The hypotenuse of a right triangle is 12...Ch. 8.R - Finding the Width of a River Find the distance...Ch. 8.R - Finding the Distance to Shore The Willis Tower in...Ch. 8.R - Finding the speed of a Glider From a glider 200...Ch. 8.R - Finding the Grade of a Mountain Trail A straight...Ch. 8.R - Finding the Height of a Helicopter Two observers...Ch. 8.R - Constructing a Highway A highway whose primary...Ch. 8.R - Prob. 34RE
Additional Math Textbook Solutions
Find more solutions based on key concepts
Two cards are randomly selected from an ordinary playing deck. What is the probability that they loin, a blackj...
A First Course in Probability (10th Edition)
Fill in each blank so that the resulting statement is true.
1. A combination of numbers, variables, and opera...
College Algebra (7th Edition)
Area Suppose that the radius r and area A = πr2 of a circle are differentiable functions of t. Write an equatio...
University Calculus: Early Transcendentals (4th Edition)
CHECK POINT I Express as a percent.
Thinking Mathematically (6th Edition)
Identifying a Test In Exercises 21–24, determine whether the hypothesis test is left-tailed, right-tailed, or t...
Elementary Statistics: Picturing the World (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 2. (i) Which of the following statements are true? Construct coun- terexamples for those that are false. (a) sequence. Every bounded sequence (x(n)) nEN C RN has a convergent sub- (b) (c) (d) Every sequence (x(n)) nEN C RN has a convergent subsequence. Every convergent sequence (x(n)) nEN C RN is bounded. Every bounded sequence (x(n)) EN CRN converges. nЄN (e) If a sequence (xn)nEN C RN has a convergent subsequence, then (xn)nEN is convergent. [10 Marks] (ii) Give an example of a sequence (x(n))nEN CR2 which is located on the parabola x2 = x², contains infinitely many different points and converges to the limit x = (2,4). [5 Marks]arrow_forward2. (i) What does it mean to say that a sequence (x(n)) nEN CR2 converges to the limit x E R²? [1 Mark] (ii) Prove that if a set ECR2 is closed then every convergent sequence (x(n))nen in E has its limit in E, that is (x(n)) CE and x() x x = E. [5 Marks] (iii) which is located on the parabola x2 = = x x4, contains a subsequence that Give an example of an unbounded sequence (r(n)) nEN CR2 (2, 16) and such that x(i) converges to the limit x = (2, 16) and such that x(i) # x() for any i j. [4 Marksarrow_forward1. (i) which are not. Identify which of the following subsets of R2 are open and (a) A = (1, 3) x (1,2) (b) B = (1,3) x {1,2} (c) C = AUB (ii) Provide a sketch and a brief explanation to each of your answers. [6 Marks] Give an example of a bounded set in R2 which is not open. (iii) [2 Marks] Give an example of an open set in R2 which is not bounded. [2 Marks]arrow_forward
- 2. if limit. Recall that a sequence (x(n)) CR2 converges to the limit x = R² lim ||x(n)x|| = 0. 818 - (i) Prove that a convergent sequence (x(n)) has at most one [4 Marks] (ii) Give an example of a bounded sequence (x(n)) CR2 that has no limit and has accumulation points (1, 0) and (0, 1) [3 Marks] (iii) Give an example of a sequence (x(n))neN CR2 which is located on the hyperbola x2 1/x1, contains infinitely many different Total marks 10 points and converges to the limit x = (2, 1/2). [3 Marks]arrow_forward3. (i) Consider a mapping F: RN Rm. Explain in your own words the relationship between the existence of all partial derivatives of F and dif- ferentiability of F at a point x = RN. (ii) [3 Marks] Calculate the gradient of the following function f: R2 → R, f(x) = ||x||3, Total marks 10 where ||x|| = √√√x² + x/2. [7 Marks]arrow_forward1. (i) (ii) which are not. What does it mean to say that a set ECR2 is closed? [1 Mark] Identify which of the following subsets of R2 are closed and (a) A = [-1, 1] × (1, 3) (b) B = [-1, 1] x {1,3} (c) C = {(1/n², 1/n2) ER2 | n EN} Provide a sketch and a brief explanation to each of your answers. [6 Marks] (iii) Give an example of a closed set which does not have interior points. [3 Marks]arrow_forward
- A company specializing in lubrication products for vintage motors produce two blended oils, Smaza and Nefkov. They make a profit of K5,000.00 per litre of Smaza and K4,000.00 per litre of Nefkov. A litre of Smaza requires 0.4 litres of heavy oil and 0.6 litres of light oil. A litre of Nefkov requires 0.8 litres of heavy oil and 0.2 litres of light oil. The company has 100 litres of heavy oil and 80 litres of light oil. How many litres of each product should they make to maximize profits and what level of profit will they obtain? Show all your workings.arrow_forward1. Show that the vector field F(x, y, z) = (2x sin ye³)ix² cos yj + (3xe³ +5)k satisfies the necessary conditions for a conservative vector field, and find a potential function for F.arrow_forward1. Newton's Law of Gravitation (an example of an inverse square law) states that the magnitude of the gravitational force between two objects with masses m and M is |F| mMG |r|2 where r is the distance between the objects, and G is the gravitational constant. Assume that the object with mass M is located at the origin in R³. Then, the gravitational force field acting on the object at the point r = (x, y, z) is given by F(x, y, z) = mMG r3 r. mMG mMG Show that the scalar vector field f(x, y, z) = = is a potential function for r √√x² + y² . Fi.e. show that F = Vf. Remark: f is the negative of the physical potential energy, because F = -V(-ƒ).arrow_forward
- 2. Suppose f(x) = 3x² - 5x. Show all your work for the problems below.arrow_forwardwrite it down for better understanding pleasearrow_forward1. Suppose F(t) gives the temperature in degrees Fahrenheit t minutes after 1pm. With a complete sentence, interpret the equation F(10) 68. (Remember this means explaining the meaning of the equation without using any mathy vocabulary!) Include units. (3 points) =arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning

Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning

Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning


Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
How to apply the law of sines to find the remaining parts of a triangle; Author: Brian McLogan;https://www.youtube.com/watch?v=NdRF18HWkmE;License: Standard YouTube License, CC-BY