
Concept explainers
(a)
The minimum speed of the swing with which Jane must begin her swing to just make it to the other side.
(a)
Answer to Problem 8.81CP
The minimum speed of the swing with which Jane must begin her swing to just make it to the other side is
Explanation of Solution
Given info: The mass of Jane is
The diagram is shown below.
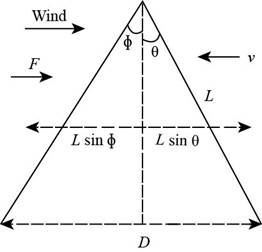
Figure I
From the figure, the width of the river is,
Here,
Rearrange the above formula for
Substitute
Thus, the value of
The formula to calculate the initial kinetic energy of Jane is,
Here,
Thus, the initial kinetic energy of Jane is
The formula to calculate the final kinetic energy of Jane is,
Here,
Substitute
Thus, the final kinetic energy of the Jane is
The formula to calculate the initial gravitational potential energy is,
Here,
Thus, the initial gravitational potential energy is
The formula to calculate the final gravitational potential energy is,
Here,
Thus the final potential energy of the car is
The formula to calculate the initial work done of the wind due to constant force is,
Here,
Substitute
Thus, the initial work done of the wind is
The formula to calculate the law of conservation of energy to the total system is,
Here,
Substitute
Substitute
Conclusion:
Therefore, the minimum speed of the swing that must Jane begin her swing to just make it to the other side is
(b)
The minimum speed of the swing at the beginning.
(b)
Answer to Problem 8.81CP
The minimum speed of the swing at the beginning is
Explanation of Solution
Given info: The mass of Jane is
The formula to calculate the combined mass is,
Here,
Substitute
The formula to calculate the initial kinetic energy is,
Here,
Thus, the initial kinetic energy is
The formula to calculate the final kinetic energy of Jane is,
Here,
Substitute
Thus, the final kinetic energy is
The formula to calculate the initial gravitational potential energy is,
Here,
Thus, the initial gravitational potential energy is
The formula to calculate the final gravitational potential energy is,
Here,
Thus the final potential energy of the car is
The formula to calculate the initial work done of the wind due to constant force is,
Here,
Substitute
Thus, the initial work done of the wind is
The formula to calculate the law of conservation of energy to the total system is,
Here,
Substitute
Substitute
Conclusion:
Therefore, the minimum speed of the swing at the beginning is
Want to see more full solutions like this?
Chapter 8 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- Four capacitors are connected as shown in the figure below. (Let C = 12.0 µF.) A circuit consists of four capacitors. It begins at point a before the wire splits in two directions. On the upper split, there is a capacitor C followed by a 3.00 µF capacitor. On the lower split, there is a 6.00 µF capacitor. The two splits reconnect and are followed by a 20.0 µF capacitor, which is then followed by point b. (a) Find the equivalent capacitance between points a and b. µF(b) Calculate the charge on each capacitor, taking ΔVab = 16.0 V. 20.0 µF capacitor µC 6.00 µF capacitor µC 3.00 µF capacitor µC capacitor C µCarrow_forwardTwo conductors having net charges of +14.0 µC and -14.0 µC have a potential difference of 14.0 V between them. (a) Determine the capacitance of the system. F (b) What is the potential difference between the two conductors if the charges on each are increased to +196.0 µC and -196.0 µC? Varrow_forwardPlease see the attached image and answer the set of questions with proof.arrow_forward
- How, Please type the whole transcript correctly using comma and periods as needed. I have uploaded the picture of a video on YouTube. Thanks,arrow_forwardA spectra is a graph that has amplitude on the Y-axis and frequency on the X-axis. A harmonic spectra simply draws a vertical line at each frequency that a harmonic would be produced. The height of the line indicates the amplitude at which that harmonic would be produced. If the Fo of a sound is 125 Hz, please sketch a spectra (amplitude on the Y axis, frequency on the X axis) of the harmonic series up to the 4th harmonic. Include actual values on Y and X axis.arrow_forwardSketch a sign wave depicting 3 seconds of wave activity for a 5 Hz tone.arrow_forward
- Sketch a sine wave depicting 3 seconds of wave activity for a 5 Hz tone.arrow_forwardThe drawing shows two long, straight wires that are suspended from the ceiling. The mass per unit length of each wire is 0.050 kg/m. Each of the four strings suspending the wires has a length of 1.2 m. When the wires carry identical currents in opposite directions, the angle between the strings holding the two wires is 20°. (a) Draw the free-body diagram showing the forces that act on the right wire with respect to the x axis. Account for each of the strings separately. (b) What is the current in each wire? 1.2 m 20° I -20° 1.2 marrow_forwardplease solve thisarrow_forward
- please solve everything in detailarrow_forward6). What is the magnitude of the potential difference across the 20-02 resistor? 10 Ω 11 V - -Imm 20 Ω 10 Ω 5.00 10 Ω a. 3.2 V b. 7.8 V C. 11 V d. 5.0 V e. 8.6 Varrow_forward2). How much energy is stored in the 50-μF capacitor when Va - V₁ = 22V? 25 µF b 25 µF 50 µFarrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





