
Concept explainers
A light rod of length 2L is free to rotate in a vertical plane about a frictionless pivot through its center. A particle of mass m1 is attached at one end of the rod, and a mass m2 is at the opposite end, where m1 > m2. The system is released from rest in the vertical position shown in Figure P8.84a, and at some later time, the system is rotating in the Position shown in Figure P8.84b. Take the reference point of the gravitational potential energy to be at the pivot, (a) Find an expression for the system's total mechanical energy in the vertical position. (b) Find an expression for the total mechanical energy in the rotated position shown in Figure P8.84b. (c) Using the fact that the mechanical energy of the system is conserved, how would you determine the angular speed co of the system in the rotated position? (d) Find the magnitude of the torque on the system in the vertical position and in the routed position. Is the torque constant? Explain what these results imply regarding the
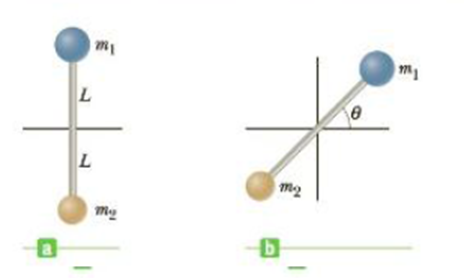
Figure P8.84
(a)
Answer to Problem 84AP
Explanation of Solution
Given Info:
The mass of the particles are m1 and m2 and light rod of length 2L . Mass m1 is attached at one end and m2 attached at other end.
In Figure P8.84 (a) the system has only potential energy and at centre the potential energy is zero since the reference point of the gravitational potential energy is at the pivot that is at the midpoint.
The formula to calculate total mechanical energy of the system about vertical position is
E=m1gL−m2gL
- g is the acceleration due to gravity
- L is the distance of the masses from the pivot
Thus, the total mechanical energy of the system about vertical position is m1gL−m2gL
Conclusion:
Therefore the total mechanical energy of the system about vertical position is m1gL−m2gL
(b)
Answer to Problem 84AP
Explanation of Solution
Given Info: The mass of the particles are m1 and m2 and light rod of length 2L . Mass m1 is attached at one end and m2 attached at other end.
In Figure P8.84 (b) the system has potential energy and rotational kinetic energy.
The expression to calculate total mechanical energy of the rotating system is,
E′=KE′+PE′
- KE′ is the rotational kinetic energy
- PE′ is the new potential energy
The potential energy of the system is given by
PE′=m1gLsinθ−m2gLsinθ (I)
The formula to calculate the rotational kinetic energy is given by
KE′=12(I1+I2)ω2
- I1 is moment of inertia of mass m1
- I2 is the moment of inertia of mass m2
- ω is the angular speed of the rotated system
The formula to calculate moment of inertia of mass m1 is
I1=m1L2
The formula to calculate moment of inertia of mass m2 is
I2=m2L2
Rewrite the above equation for KE′ using the expression for I1 and I2
KE′=12(m1L2+m2L2)ω2=12(m1+m2)L2ω2 (II)
Formula to calculate the total mechanical energy is,
E′=PE′+KE′
- E′ is the total mechanical energy at the rotated position
Substitute equation (I) and (II) in above equation to calculate E′.
E′=12(m1+m2)L2ω2+m1gLsinθ−m2gLsinθ=12(m1+m2)L2ω2+(m1−m2)gLsinθ
Conclusion: The total mechanical energy in the rotated position is 12(m1+m2)L2ω2+(m1−m2)gLsinθ
(c)
Answer to Problem 84AP
Explanation of Solution
Given Info:
According to conservation of total mechanical energy of the system, the total mechanical energy of the vertical system is same as total mechanical energy of the rotated system.
The formula to calculate total mechanical energy of the system about vertical position is
E=m1gL−m2gL
Formula to calculate the mechanical energy of the rotated system is,
E′=12(m1+m2)L2ω2+(m1−m2)gLsinθ
Equate the above expressions for E and E′ to calculate ω
12(m1+m2)L2ω2+(m1−m2)gLsinθ=m1gL−m2gL12(m1+m2)L2ω2=(m1−m2)gL(1−sinθ)ω=(2g(m1−m2)(1−sinθ)(m1+m2)L)12
Conclusion:
Therefore the angular speed of the rotated system is (2g(m1−m2)(1−sinθ)(m1+m2)L)12
(d)
Answer to Problem 84AP
Explanation of Solution
Given Info:
In the case of vertical position the gravitational force and the position of the masses from the axis of rotation lies in the same line so the net torque on the system is zero.
Formula to calculate the torque on the mass m1 is,
τ1=m1gLsin(π2−θ)=m1gLcosθ
Formula to calculate the torque on the mass m2 is,
τ2=−m2gLsin(π2−θ)=−m2gLcosθ
Formula to calculate net torque on the system is,
τ=τ1+τ2
Substitute m1gLcosθ for τ1 and −m2gLcosθ for τ2 to calculate τ
τ=m1gLcosθ−m2gLcosθ=(m1−m2)gLcosθ
Conclusion:
Therefore the net torque on the vertical system is zero and rotated system is (m1−m2)gLcosθ
Torque is not a constant therefore angular momentum will change with a non-uniform rate.
(e)
Answer to Problem 84AP
Angular acceleration has maximum value when rod is horizontal and has minimum value when rod is vertical.
Explanation of Solution
Explanation:
Given Info:
Formula to calculate the angular acceleration of the rotated system is given by
α=τ(I1+I2)
Substitute (m1−m2)gLcosθ for τ and (m1L2+m2L2) for I1+I2 in the above equation to calculate α
α=(m1−m2)gLcosθ(m1L2+m2L2)=(m1−m2)gcosθ(m1+m2)L
Thus the angular acceleration of the rotated system is ((m1−m2)gcosθ(m1+m2)L)
Conclusion:
When rod is horizontal that is θ is zero
Substitute 0 for θ in the above equation to calculate angular acceleration to calculate angular acceleration
α=((m1−m2)gcos0(m1+m2)L)=((m1−m2)g(m1+m2)L)
Angular acceleration of the rod when the rod is horizontal is ((m1−m2)g(m1+m2)L)
When rod is vertical that is θ is 90.
Substitute 0 for θ in the above equation to calculate angular acceleration to calculate angular acceleration
α=((m1−m2)gcos90(m1+m2)L)=0
Angular acceleration of the rod when the rod is vertical is 0. Therefore the rod has maximum angular acceleration when rod is horizontal. This is position corresponds to unstable equilibrium position.
Want to see more full solutions like this?
Chapter 8 Solutions
College Physics
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Concepts of Genetics (12th Edition)
Fundamentals of Physics Extended
Chemistry: The Central Science (14th Edition)
Biological Science (6th Edition)
Microbiology with Diseases by Body System (5th Edition)
- Min Min is hanging from her spring-arms off the edge of the level. Due to the spring like nature of her arms she is bouncing up and down in simple harmonic motion with a maximum displacement from equilibrium of 0.118 m. The spring constant of Min-Min’s arms is 9560. N/m and she has a mass of 87.5 kg. What is the period at which she oscillates? Find her maximum speed. Find her speed when she is located 5.00 cm from her equilibrium position.arrow_forward(a) What magnification in multiples is produced by a 0.150 cm focal length microscope objective that is 0.160 cm from the object being viewed? 15.9 (b) What is the overall magnification in multiples if an eyepiece that produces a magnification of 7.90x is used? 126 × ×arrow_forwardGravitational Potential Energyarrow_forward
- E = кедо Xo A continuous line of charge lies along the x axis, extending from x = +x to positive infinity. The line carries positive charge with a uniform linear charge density 10. (a) What is the magnitude of the electric field at the origin? (Use the following as necessary: 10, Xo, and ke.) (b) What is the direction of the electric field at the origin? O O O O O O G -y +z ○ -z +x -x +yarrow_forwardInclude free body diagramarrow_forward2 Spring 2025 -03 PITT Calculate the acceleration of a skier heading down a 10.0° slope, assuming the coefficient of cold coast at a constant velocity. You can neglect air resistance in both parts. friction for waxed wood on wet snow fly 0.1 (b) Find the angle of the slope down which this skier Given: 9 = ? 8=10° 4=0.1arrow_forward
- dry 5. (a) When rebuilding her car's engine, a physics major must exert 300 N of force to insert a c piston into a steel cylinder. What is the normal force between the piston and cyli=030 What force would she have to exert if the steel parts were oiled? k F = 306N 2 =0.03 (arrow_forwardInclude free body diagramarrow_forwardInclude free body diagramarrow_forward
- Test 2 МК 02 5. (a) When rebuilding her car's engine, a physics major must exert 300 N of force to insert a dry = 0.03 (15 pts) piston into a steel cylinder. What is the normal force between the piston and cylinder? What force would she have to exert if the steel parts were oiled? Mk Giren F = 306N MK-0.3 UK = 0.03 NF = ?arrow_forward2. A powerful motorcycle can produce an acceleration of 3.50 m/s² while traveling at 90.0 km/h. At that speed the forces resisting motion, including friction and air resistance, total 400 N. (Air resistance is analogous to air friction. It always opposes the motion of an object.) What force does the motorcycle exert backward on the ground to produce its acceleration if the mass of the motorcycle with rider is 245 ke? a = 350 m/s 2arrow_forward2. A powerful motorcycle can produce an acceleration of 3.50 m/s² while traveling at 90.0 km/h. At that speed the forces resisting motion, including friction and air resistance, total 400 N. (Air resistance is analogous to air friction. It always opposes the motion of an object.) What force does the motorcycle exert backward on the ground to produce its acceleration if the mass of the motorcycle with rider is 245 kg? (10 pts) a = 3.50 m/s 2 distance 90 km/h = 3.50m/62 M = 245garrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





