Chapter 8, Problem 7A

To determine

The decimal values of A, B, C, D and E.

Answer to Problem 7A

A $=$ $0.3$ unit.

B $=$ $0.5$ unit.

C $=$ $0.8$ unit.

D $=$ $0.92$ unit.

E $=$ $0.04$ unit.

Given information:

A scale is given as below.

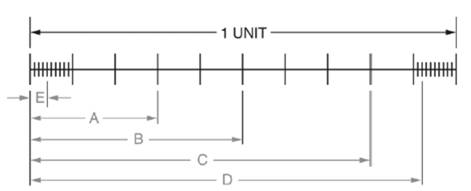
Calculation:

We have been given a scale as below.

From above scale we observe that length of scale is $1$ unit.

Distance A is equal to $3$ part out of $10$ part of the scale.

i.e. Distance A $=\frac{3}{10}\times \text{ length of scale}$

i.e. Distance A $=\frac{3}{10}\times 1=\frac{3}{10}=0.3$ unit.

Hence, A $=$ $0.3$ unit.

Similarly,

Distance B is equal to $5$ part out of $10$ part of the scale.

i.e. Distance B $=\frac{5}{10}\times \text{ length of scale}$

i.e. Distance B $=\frac{5}{10}\times 1=\frac{5}{10}=0.5$ unit.

Hence, B $=$ $0.5$ unit.

Again,

Distance C is equal to $8$ part out of $10$ part of the scale.

i.e. Distance C $=\frac{8}{10}\times \text{ length of scale}$

i.e. Distance C $=\frac{8}{10}\times 1=\frac{8}{10}=0.8$ unit.

Hence, C $=$ $0.8$ unit.

Further distance D is equal to $9$ part out of $10$ part of the scale plus $2$ parts out of $10$ parts of one-tenth of scale.

i.e. Distance D $=\frac{9}{10}\times \text{ length of scale}+\frac{2}{10}\times \frac{1}{10}$

i.e. Distance D $=\frac{9}{10}\times 1+\frac{2}{100}=0.9+0.02=0.92$ unit.

Hence, D $=$ $0.92$ unit.

Also, distance E is equal to $4$ parts out of $10$ parts of one-tenth of scale.

i.e. Distance E $=\frac{4}{10}\times \frac{1}{10}\times \text{length of scale}=\frac{4}{100}\times 1=0.04$ unit.

Hence, E $=$ $0.04$ unit.

Explanation of Solution

Given information:

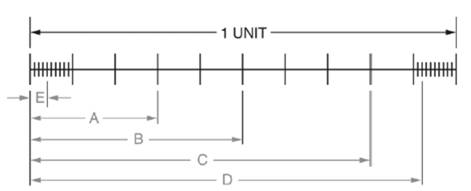
A scale is given as below.

Calculation:

We have been given a scale as below.

From above scale we observe that length of scale is $1$ unit.

Distance A is equal to $3$ part out of $10$ part of the scale.

i.e. Distance A $=\frac{3}{10}\times \text{ length of scale}$

i.e. Distance A $=\frac{3}{10}\times 1=\frac{3}{10}=0.3$ unit.

Hence, A $=$ $0.3$ unit.

Similarly,

Distance B is equal to $5$ part out of $10$ part of the scale.

i.e. Distance B $=\frac{5}{10}\times \text{ length of scale}$

i.e. Distance B $=\frac{5}{10}\times 1=\frac{5}{10}=0.5$ unit.

Hence, B $=$ $0.5$ unit.

Again,

Distance C is equal to $8$ part out of $10$ part of the scale.

i.e. Distance C $=\frac{8}{10}\times \text{ length of scale}$

i.e. Distance C $=\frac{8}{10}\times 1=\frac{8}{10}=0.8$ unit.

Hence, C $=$ $0.8$ unit.

Further distance D is equal to $9$ part out of $10$ part of the scale plus $2$ parts out of $10$ parts of one-tenth of scale.

i.e. Distance D $=\frac{9}{10}\times \text{ length of scale}+\frac{2}{10}\times \frac{1}{10}$

i.e. Distance D $=\frac{9}{10}\times 1+\frac{2}{100}=0.9+0.02=0.92$ unit.

Hence, D $=$ $0.92$ unit.

Also, distance E is equal to $4$ parts out of $10$ parts of one-tenth of scale.

i.e. Distance E $=\frac{4}{10}\times \frac{1}{10}\times \text{length of scale}=\frac{4}{100}\times 1=0.04$ unit.

Hence, E $=$ $0.04$ unit.