
Concept explainers
Draw the influence lines for the force in member AB, BG, DF, and FG.
Explanation of Solution
Calculation:
Find the support reactions.
Apply 1 k moving load from E to G in the top chord member.
Draw the free body diagram of the member as in Figure 1.
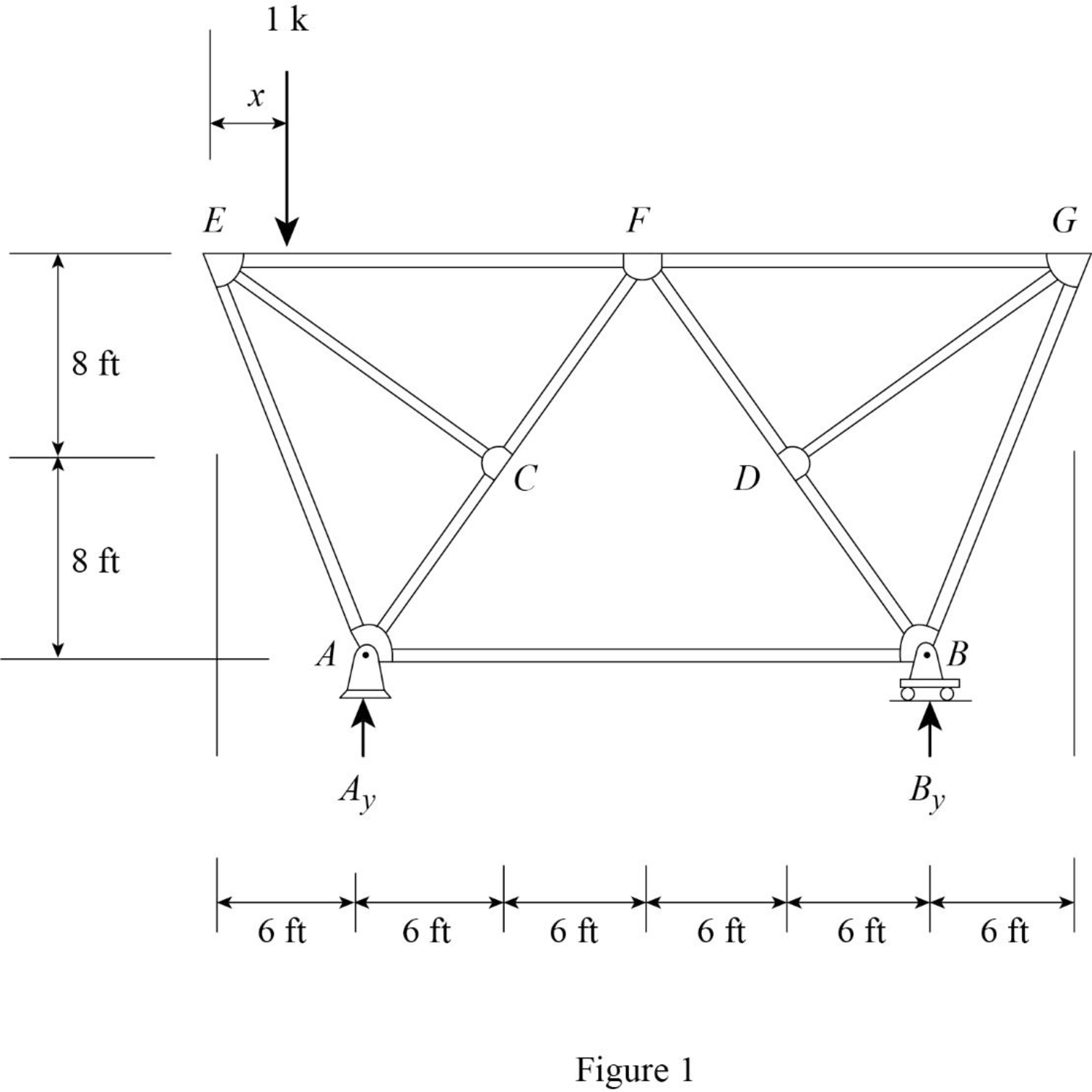
Find the reaction at A and B when 1 k load placed from E to G.
Apply moment equilibrium at A.
Apply force equilibrium equation along vertical.
Consider the upward force as positive
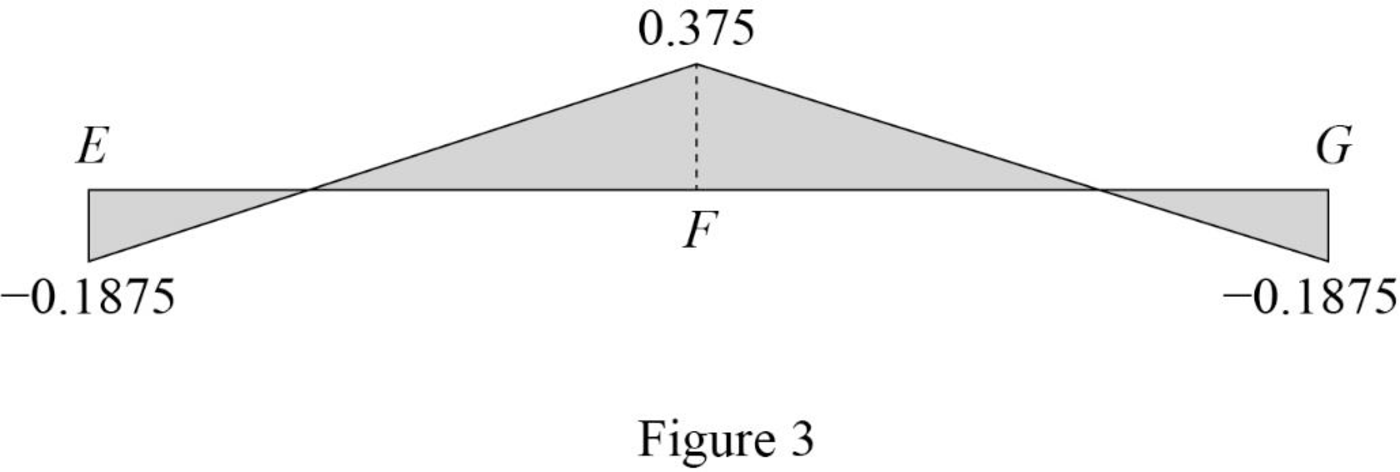
Influence line for the force in member AB.
The expressions for the member force
Draw the free body diagram of member with section aa as shown in Figure 2.

Refer Figure 2.
Find the equation of member force AB.
Apply a 1 k load at just left of F
Consider the right hand portion to section a-a.
Apply moment equilibrium equation at F.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Apply a 1 k load at just right of F
Consider the left hand portion to section a-a.
Apply moment equilibrium equation at F.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Thus, the equation of force in the member AB,
Find the force in member AB using the Equation (1) and (2) and then summarize the value in Table 1.
| x (ft) | Apply 1 k load | Force in member AB (k) | Influence line ordinate for the force in member AB (k/k) |
| 0 | E | ||
| 18 | F | 0.375 | |
| 36 | G |
Sketch the influence line diagram for ordinate for the force in member AB using Table 2 as shown in Figure 3.
Influence line for the force in member BG.
The expressions for the member force
Draw the free body diagram of section a-a as shown in Figure 4.

Refer Figure 4.
Find the force in member BG.
Apply 1 k load just left of F
Consider the section EF.
The member force of EF not affected when 1 k load applied from E to F. Therefore, the influence line ordinate of member force BG is 0 k/k from E to F.
Apply a 1 k load just the right of F
Apply moment equilibrium at F.
Consider the section right of line a-a.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Thus, the equation of force in the member BG,
Find the force in member BG using the Equation (3) and (4) and then summarize the value in Table 2.
| x (ft) | Apply 1 k load | Force in member BG (k) | Influence line ordinate for the force in member BG (k/k) |
| 0 | E | 0 | |
| 18 | F | 0 | |
| 36 | G | ‑1.07 |
Sketch the influence line diagram for ordinate for the force in member BG using Table 2 as shown in Figure 5.
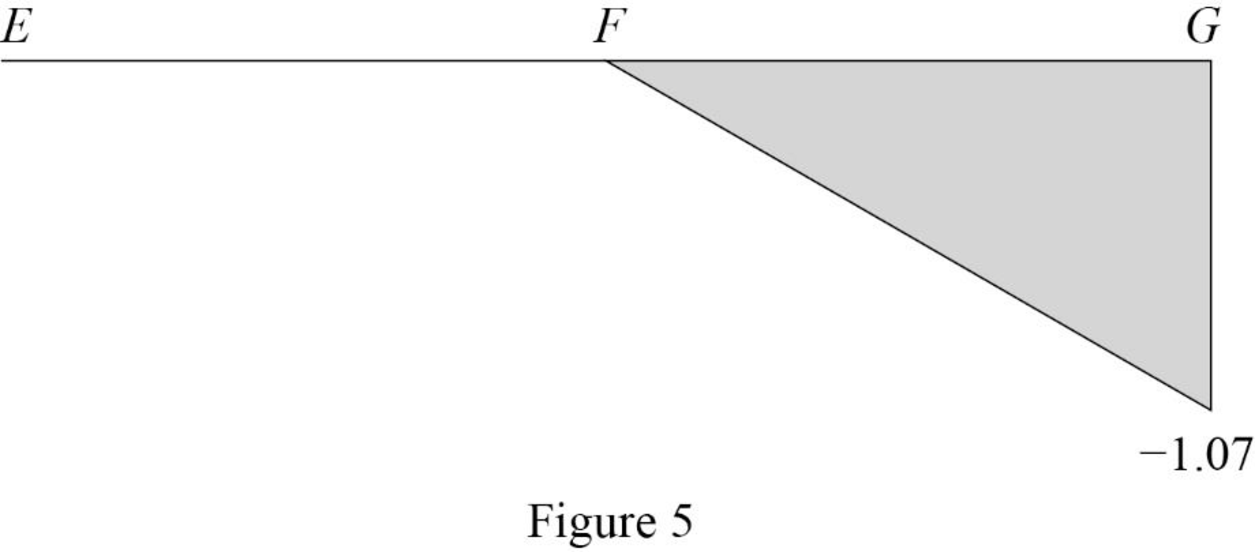
Influence line for the force in member DF.
The expressions for the member force
Draw the free body diagram of section a-a as shown in Figure 6.
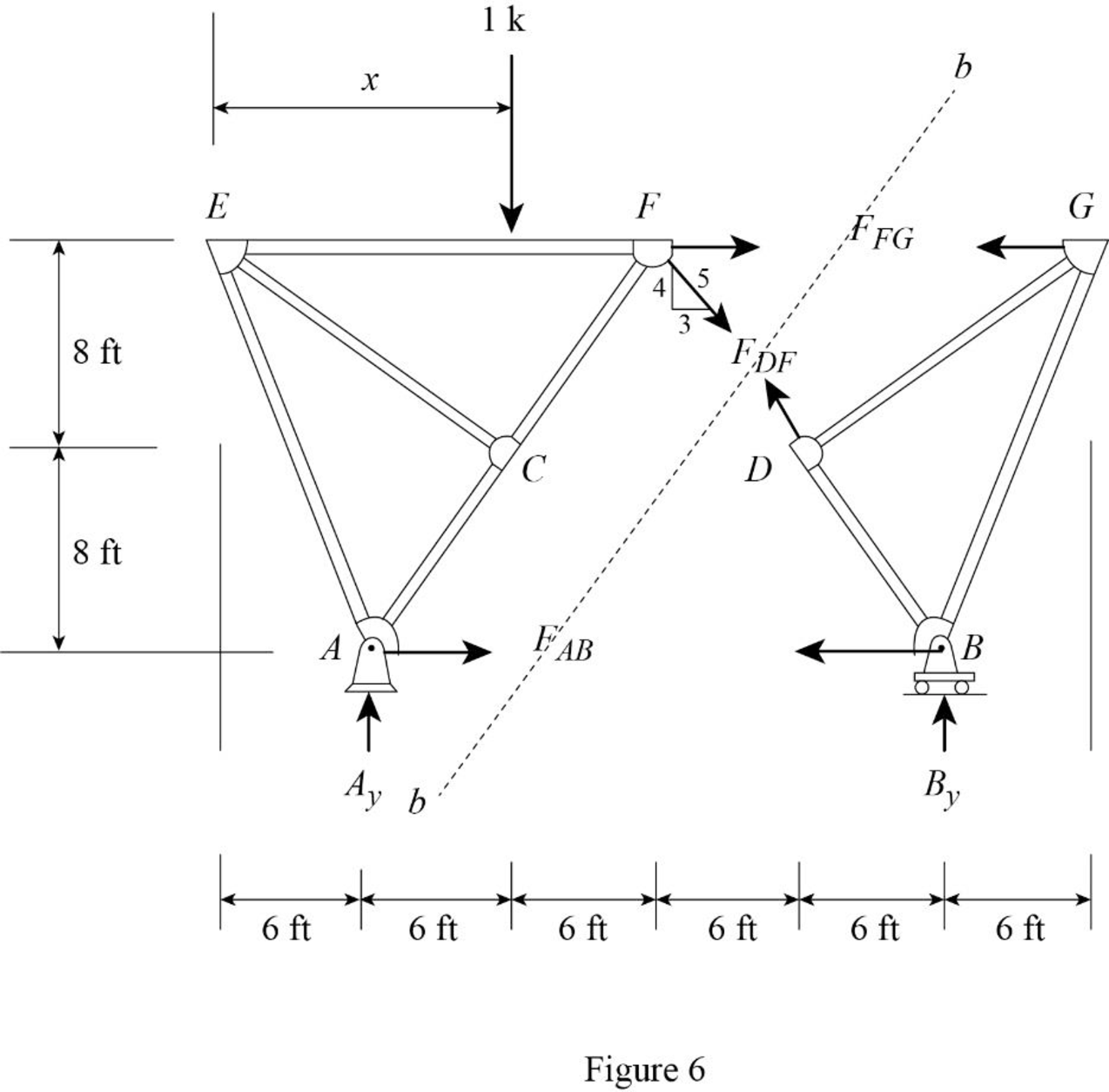
Refer Figure 6.
Find the force in member DF.
Apply 1 k load just left of F
Consider the section right of line bb.
Apply moment equilibrium at G.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Apply 1 k load just right of F
Consider the section left of line bb.
Apply moment equilibrium at E.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Thus, the equation of force in the member DF,
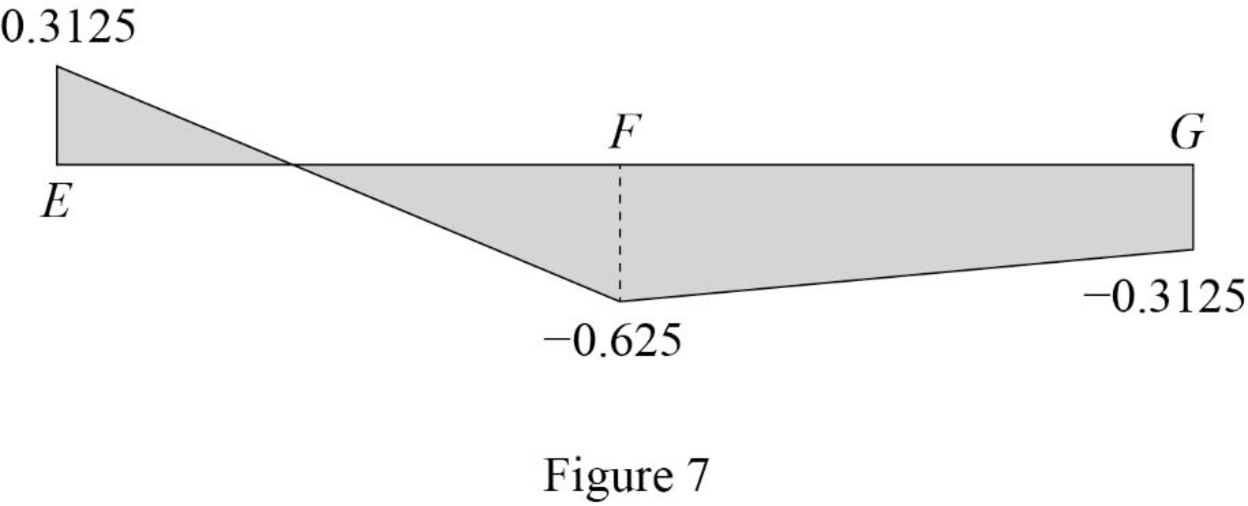
Find the force in member DF using the Equation (5) and (6) and then summarize the value in Table 3.
| x (ft) | Apply 1 k load | Force in member DF (k) | Influence line ordinate for the force in member DF (k/k) |
| 0 | E | 0.3125 | |
| 18 | F | ‑0.625 | ‑0.625 |
| 36 | G | ‑0.3125 | ‑0.3125 |
Sketch the influence line diagram for ordinate for the force in member DF using Table 3 as shown in Figure 7.
Influence line for the force in member FG.
Refer Figure 6.
Find the force in member FG.
Apply 1 k load just left of F
Consider the section right of line bb.
Apply moment equilibrium at B.
Consider clockwise moment as positive and anticlockwise moment as negative.
Apply 1 k load just right of F
Consider the section left of line bb.
Apply moment equilibrium at A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Thus, the equation of force in the member FG,
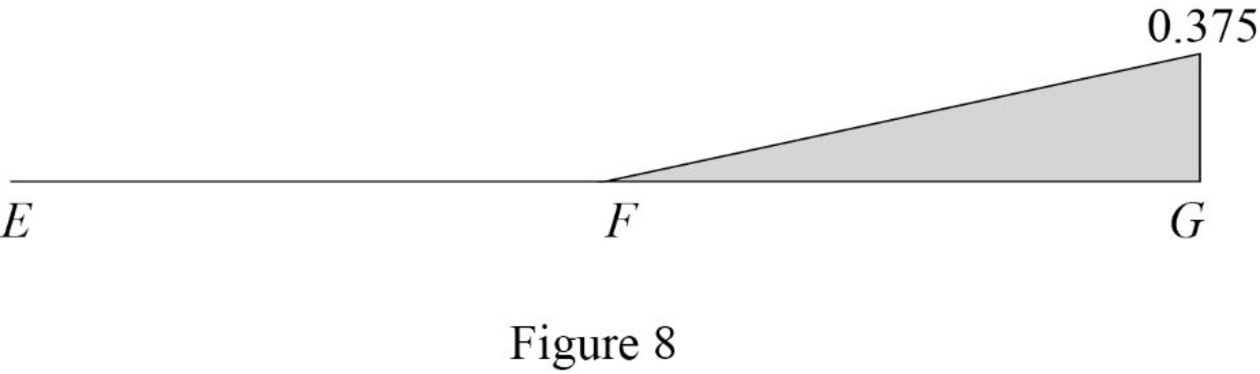
Find the force in member FG using the Equation (7) and (8) and then summarize the value in Table 4.
| x (ft) | Apply 1 k load | Force in member FG (k) | Influence line ordinate for the force in member FG (k/k) |
| 0 | E | 0.3125 | |
| 18 | F | ‑0.625 | ‑0.625 |
| 36 | G | ‑0.3125 | ‑0.3125 |
Sketch the influence line diagram for ordinate for the force in member FG using Table 4 as shown in Figure 8.
Want to see more full solutions like this?
Chapter 8 Solutions
Structural Analysis, Si Edition
- 13-31. The steel bar AB has a rectangular cross section. If it is pin connected at its ends, determine the maximum allowable intensity w of the distributed load that can be applied to BC without causing bar AB to buckle. Use a factor of safety with respect to buckling of 1.5. Est = 200 GPa, σy 360 MPa. = B W 5 m 3 m -20 mm 30 mm x x A 20 mm y Carrow_forwardProblem 1: A man-made 30 ft tall, 1.5:1 slope is to be build as shown in the figure. The soil is homogeneous with shear strength parameters c = 400 psf and φ = 290 . The moist unit weight of the soil is 119 pcf above the groundwater table and the saturated unit weight is 123 pcf below. Using the ordinary method of slices, compute the Factor of Safety (FS) along the trial failure surface shown. (Hint: Please note the unit weight is changing within the same slice.) Note 1: Use the same number of slices and dimensions as provided. Document ALL the calculations of weight (W) for each slice. Note 2: Document your solutions by following the same approach illustrated in the class, including a summary table showing all the variables and calculations involved in assessing FS.arrow_forwardhow to manually plotting by coordinatesarrow_forward
- mapping surveys/mappingarrow_forwardQuestion 3 (15pt) A traffic signal control is being designed for a four-leg intersection on a divided highway with the characteristics show in the table below. Determine an appropriate length of the yellow interval for each approach. (assuming the average vehicle length is 20ft, and the perception-reaction time is 1.0 sec, and deceleration rate of 11.2ft/sec²) Median width (ft) Number of 12ft lanes on each approach Design speed (mph) Grade North South approaches East West Approaches 18 3 45 0 10 2 35 3.5 SPEED LIMIT 45 18ft SPEED LIMIT 45 5arrow_forwardHi! Can you help me compute the concrete and masonry works for this structure based on the attached elevation drawing?The image shows the side view of a small building with labeled sections, wall openings (windows), and dimensions in centimeters. Specifically, I need help computing the following: For Concrete Works: Volume of concrete for footings, columns, and slab (if applicable) For Masonry Works (CHB Walls): Total wall area (excluding window openings) Number of CHBs required (based on 0.4 m x 0.2 m CHB) Cement and sand for block laying Cement, sand, and gravel for core filling (if reinforced) Cement and fine sand for plastering (both sides) Rebars needed for CHB reinforcement (if any) Please base it on the drawing dimensions. Let me know if additional assumptions or standards are needed (e.g., CHB size, mix ratio, thickness of plaster). Thank you!arrow_forward
- Hi! Can you help me compute the Masonry Works for the 3rd Floor only based on this image?This image shows all my completed concrete, rebar, slab, and formwork computations for the 3rd floor of a 3-storey residential building. Specifically, I need the following for CHB walls: Quantity of CHB Cement & sand for block laying (mortar) Cement, sand, and gravel for core filling Cement & fine sand for plastering Cement, sand, and gravel for CHB wall footing Number and length of vertical & horizontal rebars (10mm or as required)arrow_forwardP16.11 WP An assembly consisting of tie rod (1) and pipe strut (2) is used to support an 80 kip load, which is applied to joint B. Strut (2) is a pin-connected steel [E = 29,000 ksi] pipe with an outside diameter of 8.625 in. and a wall thickness of 0.322 in. For the loading shown in Figure P16.11, determine the factor of safety with respect to buckling for member (2). A C 24 ft B 80 kips FIGURE P16.11 12 ft 30 ftarrow_forwardHi! Based on the computations I've already completed for the second floor (shown in the attached image), can you help me compute the required materials for masonry works? Specifically, I need the following: Total quantity of CHB (Concrete Hollow Blocks) Cement and sand for block laying (mortar) Cement, sand, and gravel for CHB core filling Cement and fine sand for plastering Cement, sand, and gravel for CHB footing with pest control Reinforcing steel bars (vertical and horizontal) Please assume standard block size (e.g., 0.4m x 0.2m x 0.2m) and standard mortar/plaster thickness if not specified. Thank you!"arrow_forward
- Hi! I would like helping hand in computing all the materials needed for masonry works (CHB walls) on the ground floor. I’ve already computed the other structural elements — please refer to the attached image.arrow_forwardHi! Kindly help me compute the following based on the attached elevation plan and floor plan: Total Perimeter of the building – to be used for layouting. Total Length of Batter Board – include all sides where batter boards will be installed. Number and spacing of Stakes – assuming a stake is placed every 1.2 meters along the perimeter. Please show the complete solution and breakdown of your computation. Thank you!arrow_forwardE D (B) (<) 2945 3725 250 2225 Car Port 5000 2500 Pool Area 2 3925 3465 2875 13075 Staff Room Bar Counter 1 GROUND FLOOR PLAN SCALE 1:100 Hallway 3 1560 4125 3125 $685 Laundry & Service Area 5 A Common T&B Kitchen & Dining Arear B Living Area 2425 Terrace E 2 12150 1330 2945 4150 5480 1800 3725 1925 3800 3465 2 3 9150 4125 3575 3925 Terrace Toilet & Bathroom Toilet Bathroom Bedroom 1 Bedroom 2 SECOND FLOOR PLAN SCALE Hallway 1:100 OPEN TO BELOW E B A 3 3725 2150 1330 2945 5480 4150 1925 ⑨ 2 9150 3800 4125 3465 3575 3925 Terrace R Toilet & Bathroom Toilet & Bathroom SECOND FLOOR PLAN SCALE Hallway 1:100 OPEN TO BELOW +arrow_forward
