
| Classify angles. | (a) 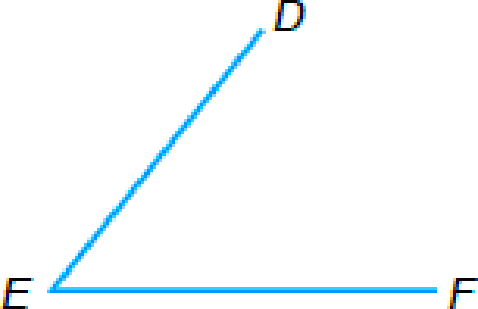 |
(a) ∡DEF is _____ |
(b) 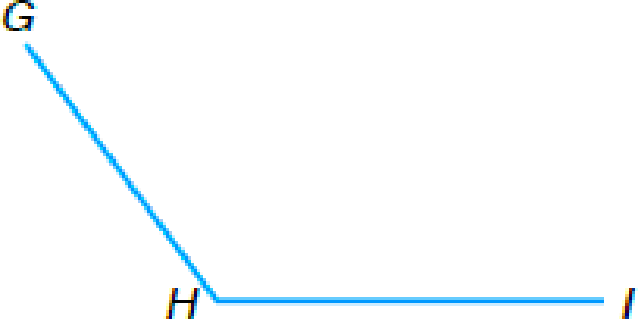 |
(b) ∡GHI is _____ | |
(c) 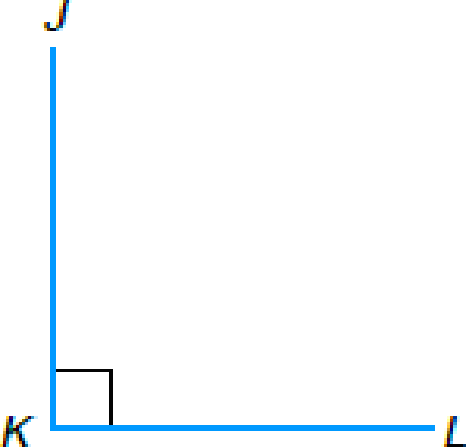 |
(c) ∡JKL is _____ |
a.
To classify: The angle DEF as acute, obtuse, or right.
Answer to Problem 2P
The angle DEF is
Explanation of Solution
Definition used:
An angle is acute when the measure of the angle is in between
An angle is right when the measure of the angle is exactly
An angle is obtuse when the measure of the angle is in between
Calculation:
Note that the measure of the given angle is less than
Thus by the above definition, the angle DEF is
b.
To classify: The angle GHI as acute, obtuse, or right.
Answer to Problem 2P
The angle GHI is
Explanation of Solution
Definition used:
An angle is said to be acute when the measure of the angle is in between
An angle is said to be right when the measure of the angle is exactly
An angle is said to be obtuse when the measure of the angle is in between
Calculation:
Note that the measure of the given angle is less than
Thus by the above definition, the angle GHI is
c.
To classify: The angle JKL as acute, obtuse, or right.
Answer to Problem 2P
The angle JKL is
Explanation of Solution
Definition used:
An angle is said to be acute when the measure of the angle is in between
An angle is said to be right when the measure of the angle is exactly
An angle is said to be obtuse when the measure of the angle is in between
Calculation:
Note that the measure of the angle JKL is exactly
Thus by the above definition, the angle JKL is
Want to see more full solutions like this?
Chapter 8 Solutions
EP MATHEMATICS FOR THE TRADES
Additional Math Textbook Solutions
Pathways To Math Literacy (looseleaf)
Elementary and Intermediate Algebra: Concepts and Applications (7th Edition)
A First Course in Probability (10th Edition)
College Algebra (7th Edition)
- Let Y be a continuous RV with PDF otherwise Find the CDF, Fry), of Y . Find an expression for pth, p € (0, 1), quantile of the distribution. Find E(Y) and V(Y). Find E(-2Y + 1) and V(-3Y - 2). Find E(Y3).arrow_forwardProvethat a) prove that for any irrational numbers there exists? asequence of rational numbers Xn converg to S. b) let S: RR be a sunctions-t. f(x)=(x-1) arc tan (x), xe Q 3(x-1) 1+x² x&Q Show that lim f(x)= 0 14x C) For any set A define the set -A=yarrow_forwardLet X be a continuous RV with CDF Find P(X < 0), P(-1 < X < 1) and P(0.5 < X). Based on your answers to the above questions, what is the median of the distribu-tion? Why Find the PDF, fx (x), of X.arrow_forwardNo chatgpt pls will upvote Already got wrong chatgpt answer Plzarrow_forwardQ2: Find the interval and radius of convergence for the following series: Σ n=1 (-1)η-1 xn narrow_forwardA survey of 581 citizens found that 313 of them favor a new bill introduced by the city. We want to find a 95% confidence interval for the true proportion of the population who favor the bill. What is the lower limit of the interval? Enter the result as a decimal rounded to 3 decimal digits. Your Answer:arrow_forwardLet X be a continuous RV with PDF where a > 0 and 0 > 0 are parameters. verify that f-∞ /x (x)dx = 1. Find the CDF, Fx (7), of X.arrow_forward6. [20] Let X be a continuous RV with PDF 2(1), 1≤x≤2 fx(x) = 0, otherwisearrow_forwardA survey of 581 citizens found that 313 of them favor a new bill introduced by the city. We want to find a 95% confidence interval for the true proportion of the population who favor the bill. What is the lower limit of the interval? Enter the result as a decimal rounded to 3 decimal digits. Your Answer:arrow_forwardA survey of 581 citizens found that 313 of them favor a new bill introduced by the city. We want to find a 95% confidence interval for the true proportion of the population who favor the bill. What is the lower limit of the interval? Enter the result as a decimal rounded to 3 decimal digits. Your Answer:arrow_forward2. The SMSA data consisting of 141 observations on 10 variables is fitted by the model below: 1 y = Bo+B1x4 + ẞ2x6 + ẞ3x8 + √1X4X8 + V2X6X8 + €. See Question 2, Tutorial 3 for the meaning of the variables in the above model. The following results are obtained: Estimate Std. Error t value Pr(>|t|) (Intercept) 1.302e+03 4.320e+02 3.015 0.00307 x4 x6 x8 x4:x8 x6:x8 -1.442e+02 2.056e+01 -7.013 1.02e-10 6.340e-01 6.099e+00 0.104 0.91737 -9.455e-02 5.802e-02 -1.630 0.10550 2.882e-02 2.589e-03 11.132 1.673e-03 7.215e-04 2.319 F) x4 1 3486722 3486722 17.9286 4.214e-05 x6 1 14595537 x8 x4:x8 x6:x8 1 132.4836 < 2.2e-16 1045693 194478 5.3769 0.02191 1 1198603043 1198603043 6163.1900 < 2.2e-16 1 25765100 25765100 1045693 Residuals 135 26254490 Estimated variance matrix (Intercept) x4 x6 x8 x4:x8 x6:x8 (Intercept) x4 x6 x8 x4:x8 x6:x8 0.18875694 1.866030e+05 -5.931735e+03 -2.322825e+03 -16.25142055 0.57188953 -5.931735e+03 4.228816e+02 3.160915e+01 0.61621781 -0.03608028 -0.00445013 -2.322825e+03…arrow_forwardIn some applications the distribution of a discrete RV, X resembles the Poisson distribution except that 0 is not a possible value of X. Consider such a RV with PMF where 1 > 0 is a parameter, and c is a constant. (a) Find the expression of c in terms of 1. (b) Find E(X). (Hint: You can use the fact that, if Y ~ Poisson(1), the E(Y) = 1.)arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
