
Concept explainers
Draw the influence lines for the shear and bending moment at point B.
Draw the influence lines for the shear at internal hinge C.
Explanation of Solution
Calculation:
Influence line for shear at point B:
Apply a 1 kN unit moving load at a distance of x from left end A.
Sketch the free body diagram of frame as shown in Figure 1.
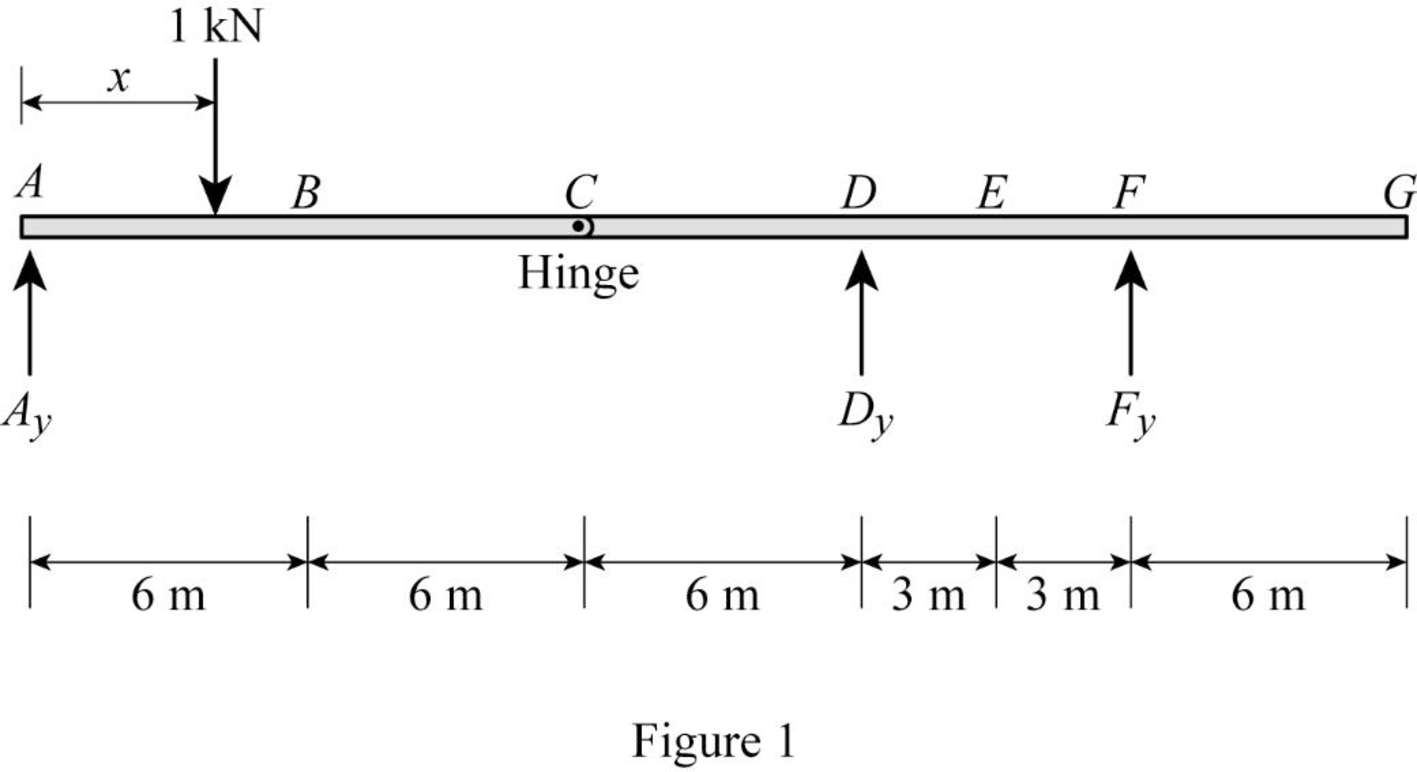
Refer Figure 1.
Consider the unit load at a variable position x to the left hinge C. (placed portion AC of the beam
Find the vertical support reaction
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Consider the unit load at a variable position x to the right hinge C. (Place portion CG of the beam
Find the vertical support reaction
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Thus, the equations of the influence line ordinate for
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction
Apply moment equilibrium at F.
Consider clockwise moment as positive and anticlockwise moment as negative.
Find the influence line ordinate of vertical reaction
Substitute
Find the influence line ordinate of vertical reaction
Substitute
Thus, the equations of the influence line ordinate for
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction
Consider the vertical forces equilibrium condition, take the upward force as positive
Find the influence line ordinate of vertical reaction
Substitute
Find the influence line ordinate of vertical reaction
Substitute
Thus, the equations of the influence line ordinate for
Find the equation of shear at B of portion AB
Sketch the free body diagram of the section AB as shown in Figure 2.
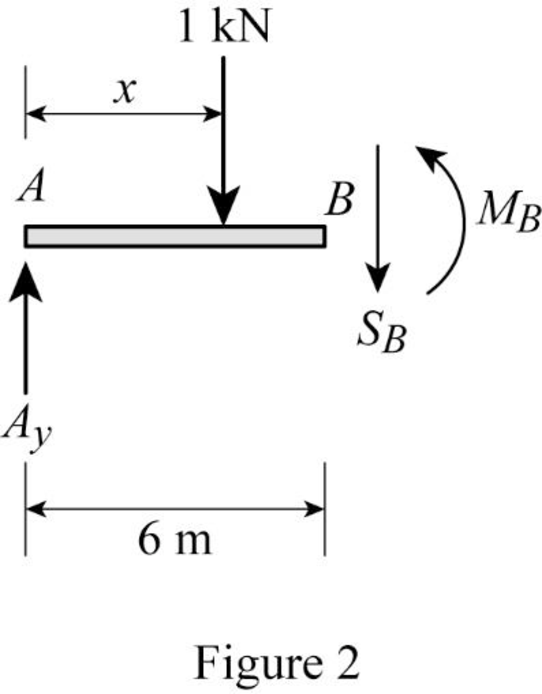
Refer Figure 2.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Find the equation of shear at B of portion BG
Sketch the free body diagram of the section BG as shown in Figure 3.
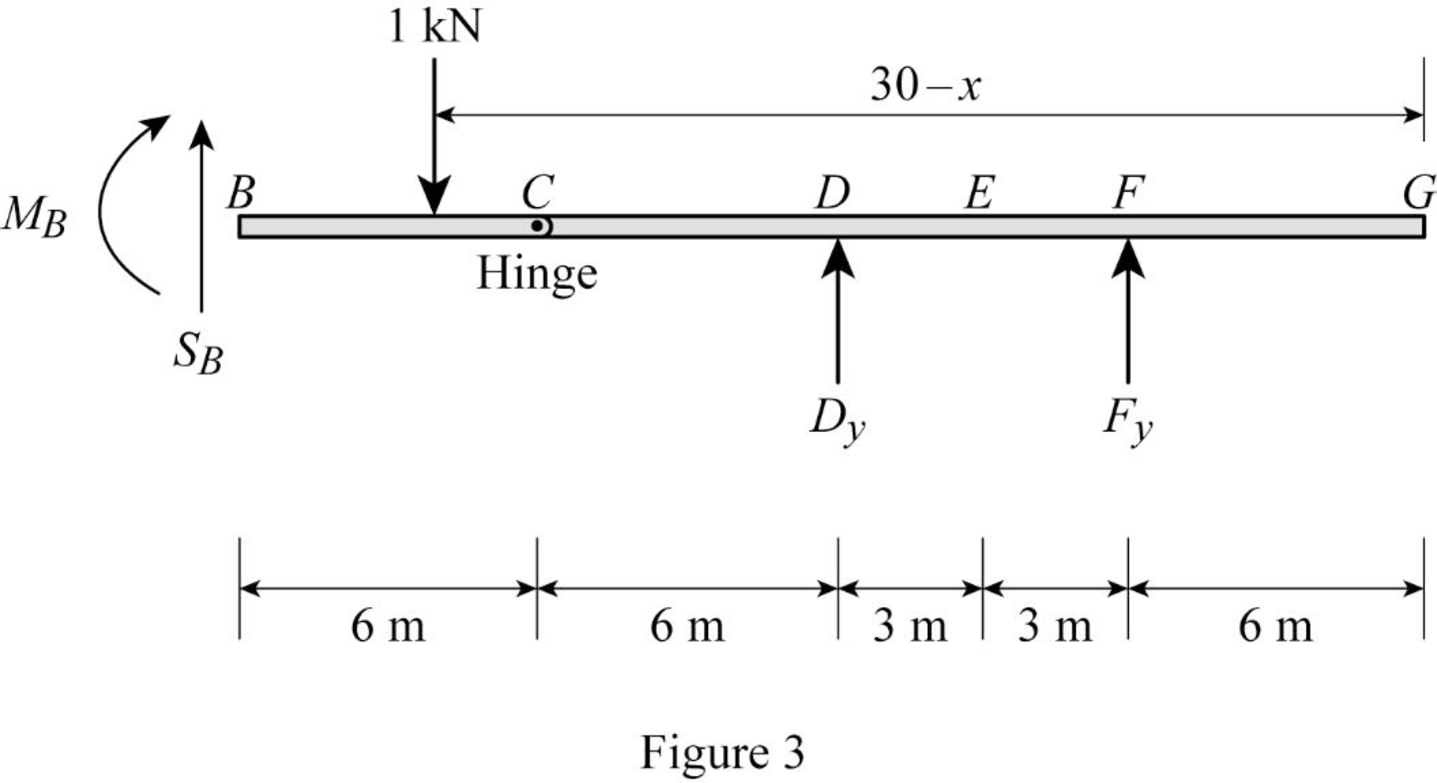
Refer Figure 3.
Apply equilibrium equation of forces.
Consider upward force as positive
Find the influence line ordinate of shear at B
Substitute
Find the influence line ordinate of shear at B
Substitute
Thus, the equations of the influence line ordinate for
Find the influence line ordinate of
| x (m) | Points | Influence line ordinate of |
| 0 | A | 0 |
| 6 | ‑0.5 | |
| 6 | 0.5 | |
| 12 | C | 0 |
| 18 | D | 0 |
| 21 | E | 0 |
| 24 | F | 0 |
| 30 | G | 0 |
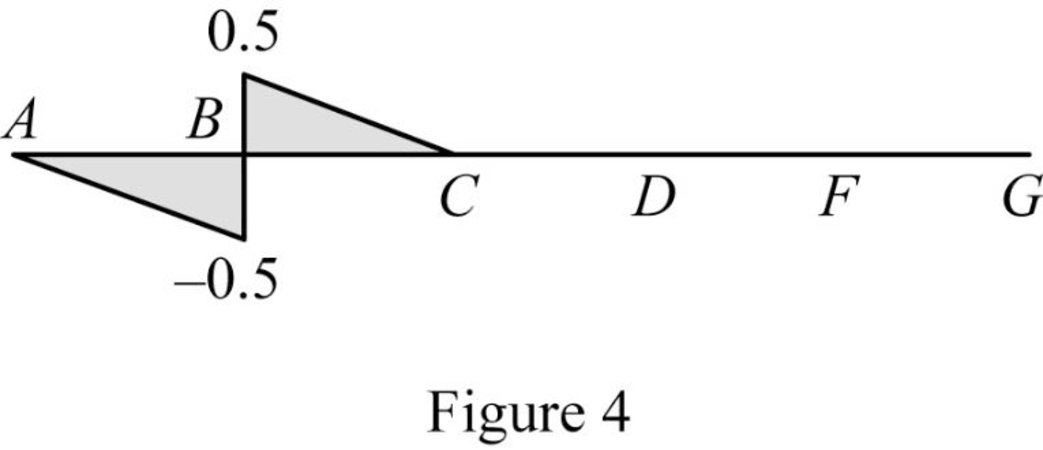
Sketch the influence line diagram for the shear at pointB as shown in Figure 4.
Influence line for moment at point B:
Refer Figure 2.
Find the equation of bending moment at B of portion AB
Take moment at B.
Consider clockwise moment as positive and anticlockwise moment as negative.
Substitute
Refer Figure 3.
Find the equation of bending moment at B of portion BG
Take moment at B.
Consider clockwise moment as negative and anticlockwise moment as positive.
Find the influence line ordinate of moment at B
Substitute
Find the influence line ordinate of moment at B
Substitute
Thus, the equations of the influence line ordinate for
Find the influence line ordinate of
| x (m) | Points | Influence line ordinate of |
| 0 | A | 0 |
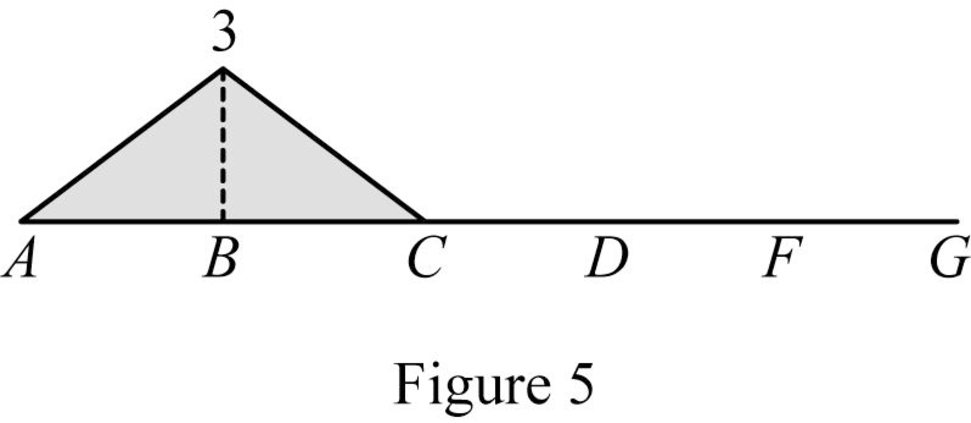
| 6 | ‑3 | |
| 12 | C | 0 |
| 18 | D | 0 |
| 21 | E | 0 |
| 24 | F | 0 |
| 30 | G | 0 |
Sketch the influence line diagram for the bending moment at point B as shown in Figure 5.
Influence line for shear at hinge C:
Apply a 1 kN unit moving load at a distance of x from left end A.
Sketch the free body diagram of frame as shown in Figure 6.
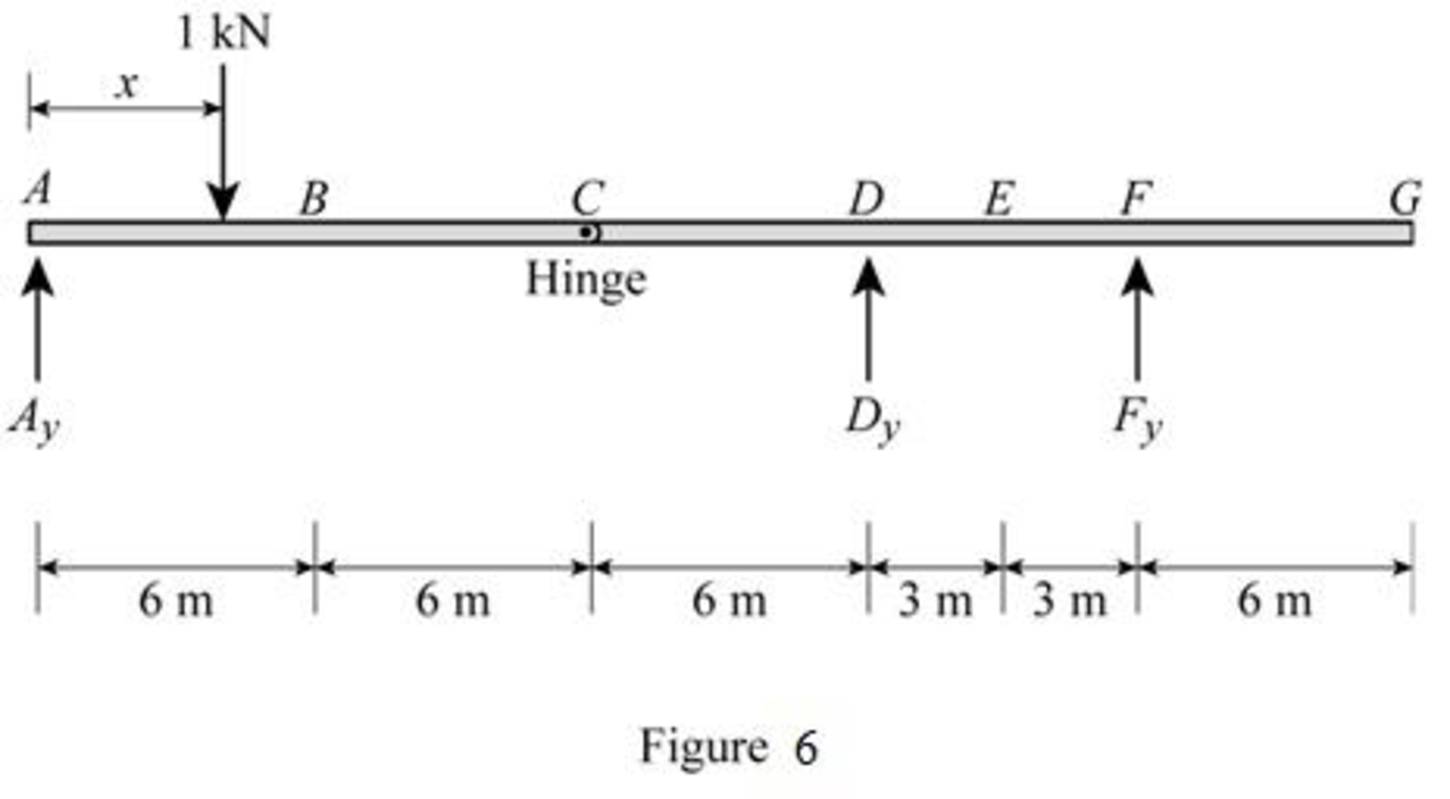
Refer Figure 6.
Consider the unit load at a variable position x to the left hinge C. (placed portion AC of the beam
Find the vertical support reaction
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Consider the unit load at a variable position x to the right hinge C. (Place portion CG of the beam
Find the vertical support reaction
Take Moment at hinge C from left end A.
Consider clockwise moment as positive and anticlockwise moment as negative.
Thus, the equations of the influence line ordinate for
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction
Apply moment equilibrium at F.
Consider clockwise moment as positive and anticlockwise moment as negative.
Find the influence line ordinate of vertical reaction
Substitute
Find the influence line ordinate of vertical reaction
Substitute
Thus, the equations of the influence line ordinate for
Refer Figure 1.
Find the equation of influence line ordinate for the vertical reaction
Consider the vertical forces equilibrium condition, take the upward force as positive
Find the influence line ordinate of vertical reaction
Substitute
Find the influence line ordinate of vertical reaction
Substitute
Thus, the equations of the influence line ordinate for
Find the equation of shear at C of portion AC
Sketch the free body diagram of the section AC as shown in Figure 7.
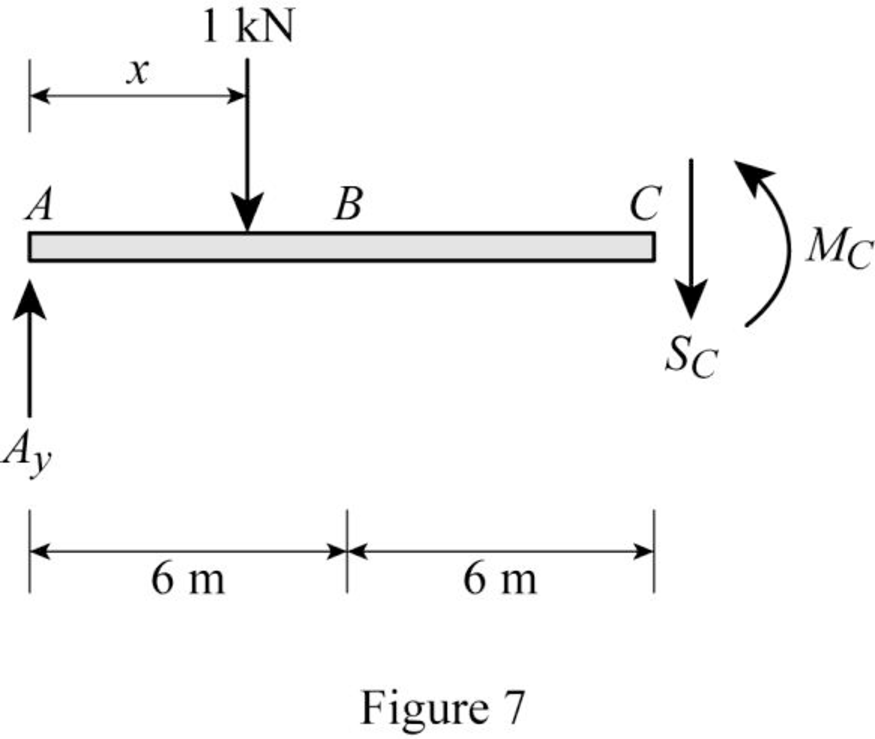
Refer Figure 7.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Find the equation of shear at C of portion CG
Sketch the free body diagram of the section CG as shown in Figure 8.
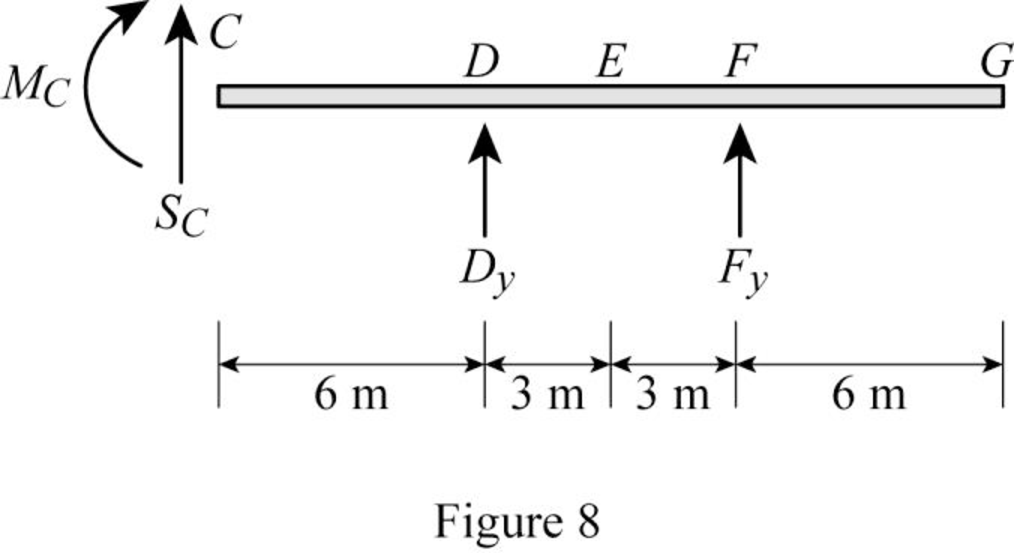
Refer Figure 8.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Thus, the equations of the influence line ordinate for
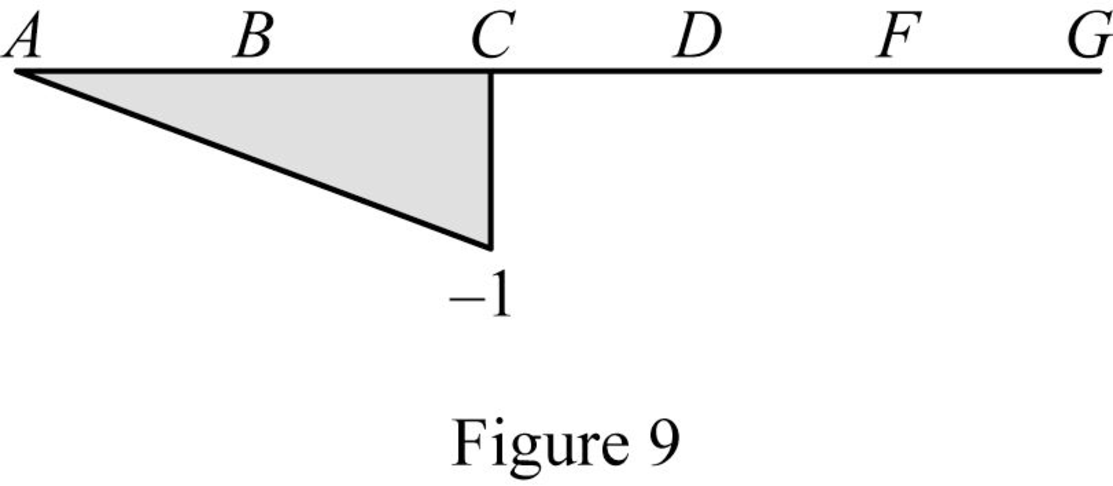
Find the influence line ordinate of
| x (m) | Points | Influence line ordinate of |
| 0 | A | 0 |
| 6 | ‑0.5 | |
| 12 | ‑1 | |
| 12 | 0 | |
| 18 | D | 0 |
| 21 | E | 0 |
| 24 | F | 0 |
| 30 | G | 0 |
Sketch the influence line diagram for the shear at point C as shown in Figure 9.
Want to see more full solutions like this?
Chapter 8 Solutions
Structural Analysis, Si Edition (mindtap Course List)
- In testing a certain kind or truck tire over rugged terrain, it is found that 20% of the trucks fail to complete the test run without a blowout. Of the next 13 trucks tested, find the probability that (a) from 2 to 6 have blowouts, (b) fewer than 4 have blowouts, and (c) more than 5 have blowouts. Click here to view page 1 of the table of binomial probability sums. Click here to view page 2 of the table of binomial probability sums. (a) The probability that from 2 to 6 trucks have blowouts is (Round to four decimal places as needed.)arrow_forwardA project requires 125 cubic yards of concrete sidewalk to be placed, for which 165 workhours have been budgeted. The latest weekly progress report shows that 78 cubic yards have been placed and 103 workhours have been expended to date. What is the status of the concrete placement? Significantly under budget. On budget. Significantly over budget. Status cannot be determined with information supplied.arrow_forwardRefer to exhibit #098. At what depth was water encountered?arrow_forward
- What is the reaction moment at A for the frame shown? a. 222.1 k-ft b. 107.8 k-ft c. 20.8 k-ft d. 23.25 k-ftarrow_forward“When a conflict exists between the project floor plans and detailed material schedule relative to size or number, which of the following usually governs in typical order of precedence?arrow_forwardWhat are the critical activitiesarrow_forward
- Approximately how many pounds of water are necessary to hydrate 100 pounds of type I Portland cement? 30 50 75 94arrow_forward7:05 3.1 Trabajo en clase.pptx .III LTE 8 Trabajo en clases 3.1 C9 X 20 W8 X 21 5-15. PL¹× 12 Fy = 50 klb/plg² KL = 16 pies KL 21 pies 2 plg MC 13 × 50 PL × 12 Fy = 42 klb/plg2 Fy = 36 klb/plg² 8 plg K k MC8 × 21.4 KL = 20 piesarrow_forwardThe steel frameword below is used to support the reinforced concrete slab used for an office area above the first storey. The slab is 210 mm thick. Sketch the loading that acts along members BE and FED. Use a = 2.15 m and b = 5.25 m. Refer to the 2024 OBC live load table. The unit weight for the concrete is 24.15 kN/m3.find:Loading for member BE Loading for member FED Live and Dead Loadsarrow_forward
- For the simply supported beam below, draw both the shear force (VFD) and ending moment (BDM) diagrams. Please show all equations and free body diagrams (FBD). Note: I want a cut through each of the three sections of the beam, with all related forces calculated and shown on the VFD and BMD.Reaction Forces Shear Force DiagramMaximum Shear ForceEquation for cut 1, 2, 3 respectively.Confirmation of Reaction ForcesBending Moment DiagramMaximum Bending Momentarrow_forwardFor the structural frame below, draw the shear force (VFD) and bending moment (BMD) diagrams for each of the three members of the frame. The frame is pin connected at A, C and D and fixed at joint B.Find:VFD & BMD for segment AB VFD & BMD for segment BCVFD & BMD for segment CD Reaction Forces VFD Equations BMD EquationsFree Body Diagramsarrow_forwardDetermine the horizontal and vertical reactions at A and C for the two member frame below. Use P1 = 3.2 kN, P2 = 14.5 kN/m, L1 = 3.3 m, and L2 = 2.3 m. Free Body DiagramsTriangular Load Use of Pin Reaction Forcesarrow_forward
