
For the digraph shown in Fig. 8-25, find
a. the indegree and outdegree of A.
b. the indegree and outdegree of B.
c. the indegree and outdegree of D.
d. the sum of the indegrees of all the vertices.
e. the sum of the outdegrees of all the vertices.
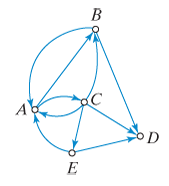
Figure 8-25
(a)
To find:
The in degree and out degree of A in the given digraph.
Answer to Problem 1E
Solution:
The in degree of A is 3 and out degree of A is 2.
Explanation of Solution
Given:
The given digraph is shown in figure (1).
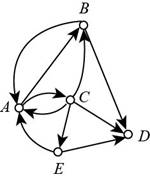
Figure (1)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (1) it can be noticed that there are 3 arcs having their ending vertex as A and 2 arcs having their starting vertex as A.
So, the indegree of A is 3 and outdegree of A is 2.
Conclusion:
Thus, the indegree of A is 3 and outdegree of A is 2.
(b)
To find:
The in degree and out degree of B in the given digraph.
Answer to Problem 1E
Solution:
The in degree of B is 2 and out degree of B is 2.
Explanation of Solution
Given:
The given digraph is shown in figure (2).
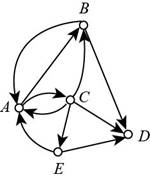
Figure (2)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (2) it can be noticed that there are 2 arcs having their ending vertex as B and 2 arcs having their starting vertex as B.
So, the indegree of B is 2 and outdegree of A is 2.
Conclusion:
Thus, the indegree of B is 2 and outdegree of B is 2.
(c)
To find:
The in degree and out degree of D in the given digraph.
Answer to Problem 1E
Solution:
The in degree of D is 3 and out degree of D is 0.
Explanation of Solution
Given:
The given digraph is shown in figure (3).
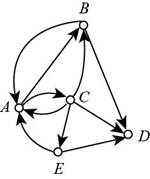
Figure (3)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (3) it can be noticed that there are 3 arcs having their ending vertex as D and no arc having their starting vertex as D.
So, the indegree of D is 3 and outdegree of D is 0.
Conclusion:
Thus, the indegree of D is 3 and outdegree of D is 0.
(d)
To find:
The sum of the in degrees of all the vertices.
Answer to Problem 1E
Solution:
The sum of all the indegrees is 10.
Explanation of Solution
Given:
The given digraph is shown in figure (4).

Figure (4)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (4) it can be noticed that there total 10 arcs, so there will be total 10 indegrees for all the vertices.
Conclusion:
Thus, the sum of all the indegrees is 10.
(e)
To find:
The sum of the out degrees of all the vertices.
Answer to Problem 1E
Solution:
The sum of all the outdegrees is 10.
Explanation of Solution
Given:
The given digraph is shown in figure (5).

Figure (5)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (5) it can be noticed that there total 10 arcs, so there will be total 10 outdegrees for all the vertices.
Conclusion:
Thus, the sum of all the outdegrees is 10.
Want to see more full solutions like this?
Chapter 8 Solutions
EXCURSIONS IN MOD.MATH W/ACCESS >BI<
- 16:39 < 文字 15:28 |美图秀秀 保存 59% 5G 46 照片 完成 Bonvicino - Period Name: 6. A right regular hexagonal pyramid with the top removed (as shown in Diagram 1) in such a manner that the top base is parallel to the base of the pyramid resulting in what is shown in Diagram 2. A wedge (from the center) is then removed from this solid as shown in Diagram 3. 30 Diogram 1 Diegrom 2. Diagram 3. If the height of the solid in Diagrams 2 and 3 is the height of the original pyramid, the radius of the base of the pyramid is 10 cm and each lateral edge of the solid in Diagram 3 is 12 cm, find the exact volume of the solid in Diagram 3, measured in cubic meters. Show all work. (T 文字 贴纸 消除笔 涂鸦笔 边框 马赛克 去美容arrow_forwardAnswer question 4 pleasearrow_forward16:39 < 文字 15:28 |美图秀秀 保存 59% 5G 46 照片 完成 Bonvicino - Period Name: 6. A right regular hexagonal pyramid with the top removed (as shown in Diagram 1) in such a manner that the top base is parallel to the base of the pyramid resulting in what is shown in Diagram 2. A wedge (from the center) is then removed from this solid as shown in Diagram 3. 30 Diogram 1 Diegrom 2. Diagram 3. If the height of the solid in Diagrams 2 and 3 is the height of the original pyramid, the radius of the base of the pyramid is 10 cm and each lateral edge of the solid in Diagram 3 is 12 cm, find the exact volume of the solid in Diagram 3, measured in cubic meters. Show all work. (T 文字 贴纸 消除笔 涂鸦笔 边框 马赛克 去美容arrow_forward
- Problem 11 (a) A tank is discharging water through an orifice at a depth of T meter below the surface of the water whose area is A m². The following are the values of a for the corresponding values of A: A 1.257 1.390 x 1.50 1.65 1.520 1.650 1.809 1.962 2.123 2.295 2.462|2.650 1.80 1.95 2.10 2.25 2.40 2.55 2.70 2.85 Using the formula -3.0 (0.018)T = dx. calculate T, the time in seconds for the level of the water to drop from 3.0 m to 1.5 m above the orifice. (b) The velocity of a train which starts from rest is given by the fol- lowing table, the time being reckoned in minutes from the start and the speed in km/hour: | † (minutes) |2|4 6 8 10 12 14 16 18 20 v (km/hr) 16 28.8 40 46.4 51.2 32.0 17.6 8 3.2 0 Estimate approximately the total distance ran in 20 minutes.arrow_forward- Let n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p − 1)/2 multiple of n, i.e. n mod p, 2n mod p, ..., p-1 2 -n mod p. Let T be the subset of S consisting of those residues which exceed p/2. Find the set T, and hence compute the Legendre symbol (7|23). 23 32 how come? The first 11 multiples of 7 reduced mod 23 are 7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8. The set T is the subset of these residues exceeding So T = {12, 14, 17, 19, 21}. By Gauss' lemma (Apostol Theorem 9.6), (7|23) = (−1)|T| = (−1)5 = −1.arrow_forwardLet n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p-1)/2 multiple of n, i.e. n mod p, 2n mod p, ..., 2 p-1 -n mod p. Let T be the subset of S consisting of those residues which exceed p/2. Find the set T, and hence compute the Legendre symbol (7|23). The first 11 multiples of 7 reduced mod 23 are 7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8. 23 The set T is the subset of these residues exceeding 2° So T = {12, 14, 17, 19, 21}. By Gauss' lemma (Apostol Theorem 9.6), (7|23) = (−1)|T| = (−1)5 = −1. how come?arrow_forward
- Shading a Venn diagram with 3 sets: Unions, intersections, and... The Venn diagram shows sets A, B, C, and the universal set U. Shade (CUA)' n B on the Venn diagram. U Explanation Check A- B Q Search 田arrow_forward3. A different 7-Eleven has a bank of slurpee fountain heads. Their available flavors are as follows: Mountain Dew, Mountain Dew Code Red, Grape, Pepsi and Mountain Dew Livewire. You fill five different cups full with each type of flavor. How many different ways can you arrange the cups in a line if exactly two Mountain Dew flavors are next to each other? 3.2.1arrow_forwardBusinessarrow_forward

 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell





