Videos
For the digraph shown in Fig. 8-25, find
a. the indegree and outdegree of A.
b. the indegree and outdegree of B.
c. the indegree and outdegree of D.
d. the sum of the indegrees of all the vertices.
e. the sum of the outdegrees of all the vertices.
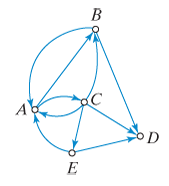
Figure 8-25
(a)
To find:
The in degree and out degree of A in the given digraph.
Answer to Problem 1E
Solution:
The in degree of A is 3 and out degree of A is 2.
Explanation of Solution
Given:
The given digraph is shown in figure (1).
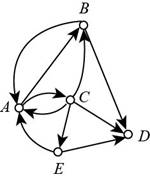
Figure (1)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (1) it can be noticed that there are 3 arcs having their ending vertex as A and 2 arcs having their starting vertex as A.
So, the indegree of A is 3 and outdegree of A is 2.
Conclusion:
Thus, the indegree of A is 3 and outdegree of A is 2.
(b)
To find:
The in degree and out degree of B in the given digraph.
Answer to Problem 1E
Solution:
The in degree of B is 2 and out degree of B is 2.
Explanation of Solution
Given:
The given digraph is shown in figure (2).
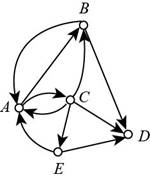
Figure (2)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (2) it can be noticed that there are 2 arcs having their ending vertex as B and 2 arcs having their starting vertex as B.
So, the indegree of B is 2 and outdegree of A is 2.
Conclusion:
Thus, the indegree of B is 2 and outdegree of B is 2.
(c)
To find:
The in degree and out degree of D in the given digraph.
Answer to Problem 1E
Solution:
The in degree of D is 3 and out degree of D is 0.
Explanation of Solution
Given:
The given digraph is shown in figure (3).
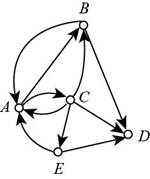
Figure (3)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (3) it can be noticed that there are 3 arcs having their ending vertex as D and no arc having their starting vertex as D.
So, the indegree of D is 3 and outdegree of D is 0.
Conclusion:
Thus, the indegree of D is 3 and outdegree of D is 0.
(d)
To find:
The sum of the in degrees of all the vertices.
Answer to Problem 1E
Solution:
The sum of all the indegrees is 10.
Explanation of Solution
Given:
The given digraph is shown in figure (4).
Figure (4)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (4) it can be noticed that there total 10 arcs, so there will be total 10 indegrees for all the vertices.
Conclusion:
Thus, the sum of all the indegrees is 10.
(e)
To find:
The sum of the out degrees of all the vertices.
Answer to Problem 1E
Solution:
The sum of all the outdegrees is 10.
Explanation of Solution
Given:
The given digraph is shown in figure (5).
Figure (5)
Definitions:
Arc:
An arc
Indegree:
For a vertex Y, the number of arcs having Y as their ending vertex is called indegree.
Outdegree:
For a vertex X, the number of arcs having X as their starting vertex is called outdegree.
Calculation:
From figure (5) it can be noticed that there total 10 arcs, so there will be total 10 outdegrees for all the vertices.
Conclusion:
Thus, the sum of all the outdegrees is 10.
Want to see more full solutions like this?
Chapter 8 Solutions
Excursions in Modern Mathematics (9th Edition)
- Solve by the quadratic formula or completing the square to obtain exact solutions. 2 e 104 OA) -16±3√6 B) 8±√10 O c) -8±√10 OD) 8±3√√6 Uarrow_forwardQuestion 14 (1 point) Listen The frame on a picture is 18 in by 22 in outside and is of uniform width. Using algebraic methods, what is the width of the frame if the inner area of the picture shown is 250 in²2? Write answer to 2 decimal places. (Write the number with no units). 18 in Your Answer: 22 inarrow_forward◄ Listen A vacant lot is being converted into a community garden. The garden and a walkway around its perimeter have an area of 560 square feet. Find the width of the walkway (x) if the garden measures 15 feet wide by 19 feet long. Write answer to 2 decimal places. (Write the number without units). X 15 feet Your Answer: 19 feet Xarrow_forward
- Listen A stuntman jumps from a roof 440 feet from the ground. How long will it take him to reach the ground? Use the formula, distance, d = 16t2, (where t is in seconds). Write answer to 1 decimal place. (Write the number, not the units). Your Answer:arrow_forwardSolve x² - 10x + 24 = 0 ○ A) 4,6 B) -12, -2 C) 12,2 D) -4, -6arrow_forwardc7. = -(9 - x) 25 A a) -1, 11 b) 31 c) 11 d) 1, 11arrow_forward
- 2 4x² - 12x-7=0 A) 7 ON 1,-1 4 OB)-, 7 1 C) 2,2 Oa½½-½ c) 17/17, - 1/1/1 D) 2, 2 ODI-,-arrow_forwardSolve using the quadratic equation formula 4x² + 12x=-6 ○ a) -12±√√3 2 b) -3±√15 -3+√15 2 ○ c) c) -3±√√√3 2 d) -3±√3 8arrow_forwardListen Solve the quadratic equation by factoring. One solution is 0. Find the other. 2x² + 16x = 0 Your Answer: Answerarrow_forward
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell