Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 78, Problem 11A
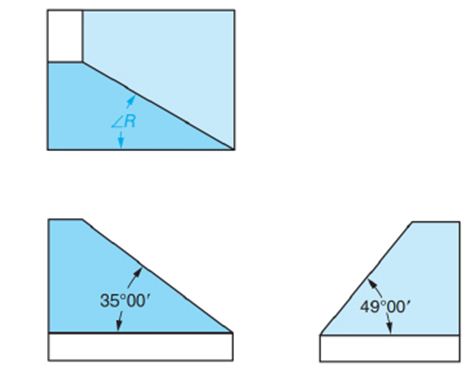
In each of Exercises 11 through 14, three views of a part are shown. Two surfaces are to be machined in reference to the horizontal plane at the angles shown in the front and right side views. Do not use intersecting angular surface formulas in solving these exercises. For each exercise:
a. Sketch and label a rectangular solid and the pyramid formed by the angular surface edges. Show the right triangle that contains
b. Compute
c. Compute
a. (sketch)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Not use ai please
O State Jordan's lemma.
Calculate the following integrals using complex variable techniques.
2π
do
(i)
1+8 cos²0'
I COS x dx
x²-2x+5°
Leave your answers in terms of real functions of real variables.
Refer to page 138 of the shared file for the numerical methods problem. Use Newton's method
to approximate the solution of the given nonlinear system of equations. Start with an initial guess
provided in the problem and iterate for at least two steps.
Link: [https://drive.google.com/file/d/1RQ2OZk-LSxpRyejKEMg1t2q15dbpVLCS/view?
usp=sharing]
Show the Jacobian matrix, iteration formulas, and each step of the computation.
Chapter 78 Solutions
Mathematics For Machine Technology
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Refer to page 128 for the heat equation problem. Solve the one-dimensional heat equation with the given initial and boundary conditions. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Use Fourier series or other appropriate methods.arrow_forwardGo to page 137 for the real analysis problem. Determine whether the given infinite series converges or diverges using appropriate convergence tests, such as the ratio test, root test, or comparison test. Justify your choice of test and provide clear steps. Link: [https://drive.google.com/file/d/1RQ2OZk-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Explain your reasoning and show all calculations.arrow_forwardRefer to page 132 of the document for the linear algebra problem. Solve the given nonhomogeneous system of equations using Gaussian elimination or matrix inverses, and express the general solution in parametric form. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Justify each step in the elimination process and interpret the solution.arrow_forward
- Tum to page 134 for the vector calculus problem. Verify Stokes' theorem by calculating the surface integral of the curl of a vector field over the given surface S and comparing it to the line integral of the same field over the boundary curve C. Link: [https://drive.google.com/file/d/1RQ2OZk-LSxpRyej KEMg1t2q15dbpVLCS/view? usp=sharing] Provide all detailed steps for calculating the curl, surface integral, and line integral.arrow_forwardThe Laplace equation problem is provided on page 136. Solve the two-dimensional Laplace equation on a rectangular region using the method of separation of variables with the specified boundary conditions. Link: [https://drive.google.com/file/d/1RQ2OZk-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Include all steps, separation constants, and final solution in series form.arrow_forwardThe dynamical systems problem is on page 127. Determine the stability of the fixed points of the given nonlinear system using linearization techniques. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Provide phase plane analysis if necessary.arrow_forward
- Refer to page 130 in the shared document for the differential equation problem. Solve the given second-order linear ordinary differential equation with the specified boundary conditions using the method of undetermined coefficients or variation of parameters as appropriate. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Show all intermediate steps, including how you satisfy the given boundary conditions.arrow_forwardWrite down the nth derivative of the function 1/z, and hence find the Taylor series of this function about the point 2 = 2. State the radius of convergence of the power series.arrow_forwardThe Laplace transform problem is on page 129. Compute the Laplace transform of the given function and find its inverse. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Present all calculations in detail and verify the result.arrow_forward
- The statistics problem is on page 95. Compute the mean (average) of the given dataset. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg 1t2q15dbpVLCS/view? usp=sharing] Show your calculations clearly.arrow_forwardRefer to page 118 for the optimization problem. Solve the constrained optimization problem using the Lagrangian method. Link: [https://drive.google.com/file/d/1RQ2OZk-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Provide all derivations and interpretations of your solution.arrow_forwardRefer to page 113 of the document for the vector calculus problem. Verify the divergence theorem for the given vector field and surface. Link: [https://drive.google.com/file/d/1RQ2OZK-LSxpRyejKEMg1t2q15dbpVLCS/view? usp=sharing] Show the calculation for both sides of the theorem.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL- Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License