Videos
For Exercises 7 through 20, compute angles to the nearer minute or hundredth degree.
Computing Angles of Rotation and Tilt Without Using Machining Formulas
Three views of a rectangular solid block are shown in which a compound-angular surface is to be machined. A pictorial view of the block with auxiliary lines required for computations is also shown. Do not use machining formulas in solving these exercises. For each of Exercises 7 through 10
a. Determine the angle of rotation,
b. Determine the angle of tilt,
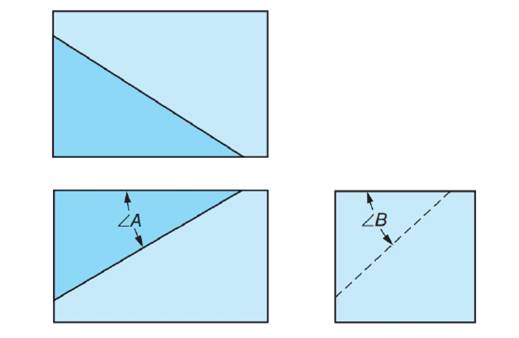
Given:
Want to see the full answer?
Check out a sample textbook solution
Chapter 77 Solutions
Mathematics For Machine Technology
- Consider the initial value problem y"+y'-12y= 0, y(0) = a, y'(0) = 4 Find the value of a so that the solution to the initial value problem approaches zero as too a =arrow_forwardConsider the initial value problem y"+y'-12y= 0, y(0) = a, y'(0) = 4 Find the value of a so that the solution to the initial value problem approaches zero as too a =arrow_forward2 x²+1 dx x47x²+1arrow_forward
- Your employer automatically puts 5 percent of your salary into a 401(k) retirement account each year. The account earns 10% interest. Suppose you just got the job, your starting salary is $60000, and you expect to receive a 2.5% raise each year. For simplicity, assume that interest earned and your raises are given as nominal rates and compound continuously. Find the value of your retirement account after 20 yearsarrow_forwardCompute the principal values of i¹² (i — 1)² and (i(i − 1))². - -arrow_forward1 2 3 Consider the matrix A = 0 4 5. Give an example of 006 (a) a nonzero matrix B for which det(A + B) = det(A) + det(B); (b) a matrix C for which det(A+C)det(A) + det(C).arrow_forward
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage LearningMathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage