
Population distribution. In order to study the population distribution of a certain species of insect, a biologist has constructed an artificial habitat in the shape of a rectangle 16 feet long and 12 feet wide. The only food available to the insects in this habitat is located at its center. The biologist has determined that the concentration C of insects per square foot at a point d units from the food supply (see the figure) is given approximately by
What is the average concentration of insects throughout the habitat? Express C as a function of x and y, set up a double
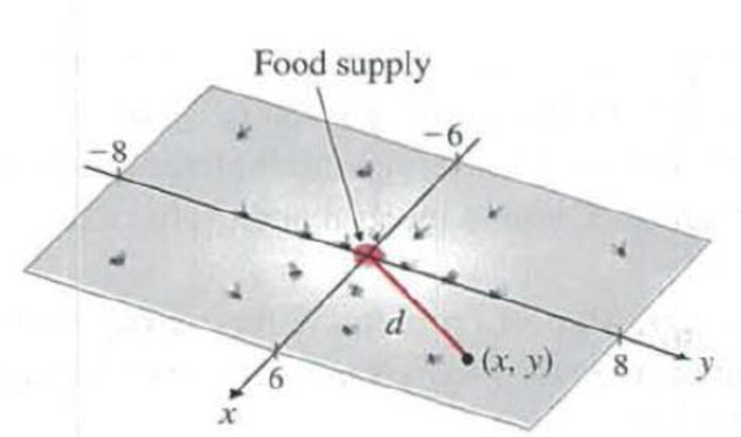
Figure of 51
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
- What is the area of this figure? 7 mi 3 mi 8 mi 5 mi 2 mi 6 mi 3 mi 9 miarrow_forward10) Multiply (8m + 3)² A) 8m²+11m+6 B) m² + 48m+9 C) 64m²+48m+9 D) 16m²+11m+6arrow_forwardQ/ Solving Laplace equation on a Rectangular Rejon uxxuyy = o u(x, 0) = f(x) исх, 6) = д(х) b) u Co,y) = u(a,y) = =0arrow_forward
- Q/solve the heat equation initial-boundary-value problem- u+= 2uxx 4 (x10) = x+\ u (o,t) = ux (4,t) = 0arrow_forwardnot use ai pleasearrow_forwardA graph of the function f is given below: Study the graph of ƒ at the value given below. Select each of the following that applies for the value a = 1 Of is defined at a. If is not defined at x = a. Of is continuous at x = a. If is discontinuous at x = a. Of is smooth at x = a. Of is not smooth at = a. If has a horizontal tangent line at = a. f has a vertical tangent line at x = a. Of has a oblique/slanted tangent line at x = a. If has no tangent line at x = a. f(a + h) - f(a) lim is finite. h→0 h f(a + h) - f(a) lim h->0+ and lim h h->0- f(a + h) - f(a) h are infinite. lim does not exist. h→0 f(a+h) - f(a) h f'(a) is defined. f'(a) is undefined. If is differentiable at x = a. If is not differentiable at x = a.arrow_forward
- The graph below is the function f(z) 4 3 -2 -1 -1 1 2 3 -3 Consider the function f whose graph is given above. (A) Find the following. If a function value is undefined, enter "undefined". If a limit does not exist, enter "DNE". If a limit can be represented by -∞o or ∞o, then do so. lim f(z) +3 lim f(z) 1-1 lim f(z) f(1) = 2 = -4 = undefined lim f(z) 1 2-1 lim f(z): 2-1+ lim f(x) 2+1 -00 = -2 = DNE f(-1) = -2 lim f(z) = -2 1-4 lim f(z) 2-4° 00 f'(0) f'(2) = = (B) List the value(s) of x for which f(x) is discontinuous. Then list the value(s) of x for which f(x) is left- continuous or right-continuous. Enter your answer as a comma-separated list, if needed (eg. -2, 3, 5). If there are none, enter "none". Discontinuous at z = Left-continuous at x = Invalid use of a comma.syntax incomplete. Right-continuous at z = Invalid use of a comma.syntax incomplete. (C) List the value(s) of x for which f(x) is non-differentiable. Enter your answer as a comma-separated list, if needed (eg. -2, 3, 5).…arrow_forwardA graph of the function f is given below: Study the graph of f at the value given below. Select each of the following that applies for the value a = -4. f is defined at = a. f is not defined at 2 = a. If is continuous at x = a. Of is discontinuous at x = a. Of is smooth at x = a. f is not smooth at x = a. If has a horizontal tangent line at x = a. f has a vertical tangent line at x = a. Of has a oblique/slanted tangent line at x = a. Of has no tangent line at x = a. f(a + h) − f(a) h lim is finite. h→0 f(a + h) - f(a) lim is infinite. h→0 h f(a + h) - f(a) lim does not exist. h→0 h f'(a) is defined. f'(a) is undefined. If is differentiable at x = a. If is not differentiable at x = a.arrow_forwardFind the point of diminishing returns (x,y) for the function R(X), where R(x) represents revenue (in thousands of dollars) and x represents the amount spent on advertising (in thousands of dollars). R(x) = 10,000-x3 + 42x² + 700x, 0≤x≤20arrow_forward
- [3] Use a substitution to rewrite sn(x) as 8n(x) = 1 2π C sin 2n+1 sin f(x+u)du.arrow_forwardDifferentiate the following functions. (a) y(x) = x³+6x² -3x+1 (b) f(x)=5x-3x (c) h(x) = sin(2x2)arrow_forwardx-4 For the function f(x): find f'(x), the third derivative of f, and f(4) (x), the fourth derivative of f. x+7arrow_forward

 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill





