Student Solutions Manual for Calculus & Its Applications and Calculus & Its Applications, Brief Version
14th Edition
ISBN: 9780134463230
Author: Larry J. Goldstein, David I Lay, David I. Schneider, Nakhle H. Asmar
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 7.5, Problem 1E
To determine
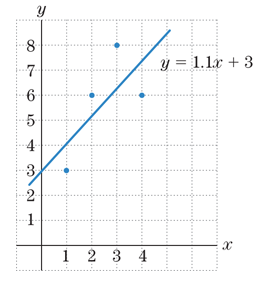
The least-square error
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(1) Write the following quadratic equation in terms of the vertex coordinates.
The final answer is 8/π(sinx) + 8/3π(sin 3x)+ 8/5π(sin5x)....
Keity
x२
1. (i)
Identify which of the following subsets of R2 are open and which
are not.
(a)
A = (2,4) x (1, 2),
(b)
B = (2,4) x {1,2},
(c)
C = (2,4) x R.
Provide a sketch and a brief explanation to each of your answers.
[6 Marks]
(ii)
Give an example of a bounded set in R2 which is not open.
[2 Marks]
(iii)
Give an example of an open set in R2 which is not bounded.
[2 Marks
Chapter 7 Solutions
Student Solutions Manual for Calculus & Its Applications and Calculus & Its Applications, Brief Version
Ch. 7.1 - Let f(x,y,z)=x2+y(xz)4. Compute f(3,5,2).Ch. 7.1 - Prob. 2CYUCh. 7.1 - Let f(x,y)=x23xyy2. Compute f(5,0),f(5,2) and...Ch. 7.1 - Prob. 2ECh. 7.1 - Let g(x,y,z)=x/(yz). Compute g(1,1),g(0,1) and...Ch. 7.1 - Let f(x,y,z)=x2ey2+z2. Compute f(1,1,1) and...Ch. 7.1 - Let f(x,y)=xy. Show that f(2+h,3)f(2,3)=3h.Ch. 7.1 - Let f(x,y)=xy. Show that f(2,3+k)f(2,3)=2k.Ch. 7.1 - Cost Find a formula C(x,y,z) that gives the cost...Ch. 7.1 - Cost Find a formula C(x,y,z) that gives the cost...
Ch. 7.1 - Consider the cobb-Douglas production function...Ch. 7.1 - Let f(x,y)=10x25y35. Show that f(3a,3b)=3f(a,b).Ch. 7.1 - Present value The present value of A dollars to be...Ch. 7.1 - Refer to Example 3. If labor costs $100 per unit...Ch. 7.1 - Tax and Homeowner Exemption The value of...Ch. 7.1 - Tax and Homeowner Exemption Let f(r,v,x) be the...Ch. 7.1 - Draw the level curve of height 0,1 and 2 for the...Ch. 7.1 - Draw the level curve of height 0,1 and 2 for the...Ch. 7.1 - Draw the level curve of function f(x,y)=xy...Ch. 7.1 - Draw the level curve of function f(x,y)=xy...Ch. 7.1 - Find the function f(x,y) that has line y=3x4 as a...Ch. 7.1 - Find the function f(x,y) that has the curve y=2x2...Ch. 7.1 - Suppose that a topographic map is viewed as the...Ch. 7.1 - Isocost Lines A certain production process uses...Ch. 7.1 - Match the graphs of the functions in Exercises...Ch. 7.1 - Match the graphs of the functions in Exercises...Ch. 7.1 - Match the graphs of the functions in Exercises...Ch. 7.1 - Match the graphs of the functions in Exercises...Ch. 7.2 - The number of TV sets an appliance store sells per...Ch. 7.2 - The monthly mortgage payment for a house is a...Ch. 7.2 - Find fxandfy for each of the following functions....Ch. 7.2 - Prob. 2ECh. 7.2 - Find fxandfy for each of the following function....Ch. 7.2 - Find fxandfy for each of the following function....Ch. 7.2 - Find fxandfy for each of the following function....Ch. 7.2 - Prob. 6ECh. 7.2 - Find fxandfy for each of the following function....Ch. 7.2 - Find fxandfy for each of the following function....Ch. 7.2 - Find fxandfy for each of the following function....Ch. 7.2 - Find fxandfy for each of the following function....Ch. 7.2 - Find fxandfy for each of the following function....Ch. 7.2 - Find fxandfy for each of the following function....Ch. 7.2 - Prob. 13ECh. 7.2 - Let f(p,q)=1p(1+q). Find fq and fp.Ch. 7.2 - Let f(x,y,z)=(1+x2y)/z. fx,fy,andfz.Ch. 7.2 - Prob. 16ECh. 7.2 - Let f(x,y,z)=xzeyz. Find fx,fy,andfz.Ch. 7.2 - Let f(x,y,z)=xyz. Find fx,fz,andfz.Ch. 7.2 - Let f(x,y,z)=x2+2xy+y2+3x+5y. Find...Ch. 7.2 - Prob. 20ECh. 7.2 - Let f(x,y)=xy2+5. Evaluate fy at (x,y)=(2,1) and...Ch. 7.2 - Prob. 22ECh. 7.2 - Prob. 23ECh. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - ProductivityLabor and Capital The productivity of...Ch. 7.2 - Prob. 27ECh. 7.2 - Prob. 28ECh. 7.2 - Let p1 be the average price of MP3 players, p2 the...Ch. 7.2 - Prob. 30ECh. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Prob. 34ECh. 7.2 - Prob. 35ECh. 7.2 - Compute 2fy2, where f(x,y)=60x3/4y1/4, a...Ch. 7.2 - Prob. 37ECh. 7.2 - Prob. 38ECh. 7.3 - Prob. 1CYUCh. 7.3 - Prob. 2CYUCh. 7.3 - Prob. 1ECh. 7.3 - Find all points (x,y) where f(x,y) has a possible...Ch. 7.3 - Prob. 3ECh. 7.3 - Prob. 4ECh. 7.3 - Prob. 5ECh. 7.3 - Prob. 6ECh. 7.3 - Prob. 7ECh. 7.3 - Find all points (x,y) where f(x,y) has a possible...Ch. 7.3 - Find all points (x,y) where f(x,y) has a possible...Ch. 7.3 - Find all points (x,y) where f(x,y) has a possible...Ch. 7.3 - Find all points (x,y) where f(x,y) has a possible...Ch. 7.3 - Find all points (x,y) where f(x,y) has a possible...Ch. 7.3 - Find all points (x,y) where f(x,y) has a possible...Ch. 7.3 - Prob. 14ECh. 7.3 - Prob. 15ECh. 7.3 - Find all points (x,y) where f(x,y) has a possible...Ch. 7.3 - Prob. 17ECh. 7.3 - The function f(x,y)=12x2+2xy+9+3y2x+2y has a...Ch. 7.3 - Prob. 19ECh. 7.3 - Prob. 20ECh. 7.3 - Prob. 21ECh. 7.3 - Prob. 22ECh. 7.3 - Prob. 23ECh. 7.3 - Prob. 24ECh. 7.3 - Prob. 25ECh. 7.3 - Find all points (x,y) where f(x,y) has a possible...Ch. 7.3 - Prob. 27ECh. 7.3 - Find all points (x,y) where f(x,y) has a possible...Ch. 7.3 - Prob. 29ECh. 7.3 - Prob. 30ECh. 7.3 - Prob. 31ECh. 7.3 - Prob. 32ECh. 7.3 - Prob. 33ECh. 7.3 - Prob. 34ECh. 7.3 - Find all points f(x,y) has a possible relative...Ch. 7.3 - Prob. 36ECh. 7.3 - Find all points f(x,y) has a possible relative...Ch. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - Find all points f(x,y) has a possible relative...Ch. 7.3 - Prob. 41ECh. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - Find all points f(x,y) has a possible relative...Ch. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - Prob. 48ECh. 7.3 - Prob. 49ECh. 7.3 - Minimizing Surface Area Find the dimensions of the...Ch. 7.3 - Maximizing Profit A company manufactures and sells...Ch. 7.3 - Maximizing Profit A monopolist manufactures and...Ch. 7.3 - Prob. 53ECh. 7.3 - Revenue from Two Products A company manufactures...Ch. 7.4 - Prob. 1CYUCh. 7.4 - Refer to Exercise 29 of Section 7.3. What is the...Ch. 7.4 - Prob. 1ECh. 7.4 - Prob. 2ECh. 7.4 - Prob. 3ECh. 7.4 - Prob. 4ECh. 7.4 - Prob. 5ECh. 7.4 - Prob. 6ECh. 7.4 - Prob. 7ECh. 7.4 - Prob. 8ECh. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Prob. 11ECh. 7.4 - Prob. 12ECh. 7.4 - Prob. 13ECh. 7.4 - Prob. 14ECh. 7.4 - Prob. 15ECh. 7.4 - Prob. 16ECh. 7.4 - Prob. 17ECh. 7.4 - Solve the following exercises by the method of...Ch. 7.4 - Prob. 19ECh. 7.4 - Solve the following exercises by the method of...Ch. 7.4 - Prob. 21ECh. 7.4 - Prob. 22ECh. 7.4 - Solve the following exercises by the method of...Ch. 7.4 - Solve the following exercises by the method of...Ch. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - Prob. 30ECh. 7.4 - Prob. 31ECh. 7.4 - Use Lagrange multipliers to find the three...Ch. 7.4 - Minimizing Surface Area Find the dimensions of an...Ch. 7.4 - Maximizing Volume A shelter for use at the beach...Ch. 7.4 - Prob. 35ECh. 7.4 - Prob. 36ECh. 7.5 - Prob. 1CYUCh. 7.5 - Prob. 2CYUCh. 7.5 - Prob. 1ECh. 7.5 - Find the least-squares error E for the...Ch. 7.5 - Prob. 3ECh. 7.5 - Prob. 4ECh. 7.5 - Prob. 5ECh. 7.5 - Prob. 6ECh. 7.5 - Prob. 7ECh. 7.5 - Prob. 8ECh. 7.5 - Prob. 9ECh. 7.5 - Prob. 10ECh. 7.5 - In the remaining exercises, use one or more of the...Ch. 7.5 - In the remaining exercises, use one or more of the...Ch. 7.5 - Prob. 13ECh. 7.5 - Prob. 14ECh. 7.5 - Prob. 15ECh. 7.6 - Calculate the iterated integral 02(0x/2e2yxdy)dx.Ch. 7.6 - Prob. 2CYUCh. 7.6 - Prob. 1ECh. 7.6 - Prob. 2ECh. 7.6 - Prob. 3ECh. 7.6 - Calculate the following iterated integrals....Ch. 7.6 - Prob. 5ECh. 7.6 - Calculate the following iterated integrals....Ch. 7.6 - Calculate the following iterated integrals....Ch. 7.6 - Calculate the following iterated integrals....Ch. 7.6 - Prob. 9ECh. 7.6 - Prob. 10ECh. 7.6 - Prob. 11ECh. 7.6 - Prob. 12ECh. 7.6 - Prob. 13ECh. 7.6 - Calculate the volumes over the following regions R...Ch. 7 - Give an example of a level curve of a function of...Ch. 7 - Prob. 2CCECh. 7 - Prob. 3CCECh. 7 - Prob. 4CCECh. 7 - Prob. 5CCECh. 7 - Prob. 6CCECh. 7 - Prob. 7CCECh. 7 - State the second derivative test for functions of...Ch. 7 - Prob. 9CCECh. 7 - Prob. 10CCECh. 7 - Prob. 11CCECh. 7 - Give a formula for evaluating a double integral in...Ch. 7 - Let f(x,y)=xy/(1+x). Compute f(2,9),f(5,1), and...Ch. 7 - Prob. 2RECh. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - Prob. 14RECh. 7 - Prob. 15RECh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - In Exercises 1720, find all points (x,y) where...Ch. 7 - Prob. 19RECh. 7 - In Exercises 1720, find all points (x,y) where...Ch. 7 - In Exercises 2123, find all points (x,y) where...Ch. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Find the values of x,y,z at which...Ch. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Use the method of Lagrange multiplier to: A person...Ch. 7 - Use the method of Lagrange multiplier to: The...Ch. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - Prob. 34RECh. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 2. (i) Which of the following statements are true? Construct coun- terexamples for those that are false. (a) sequence. Every bounded sequence (x(n)) nEN C RN has a convergent sub- (b) (c) (d) Every sequence (x(n)) nEN C RN has a convergent subsequence. Every convergent sequence (x(n)) nEN C RN is bounded. Every bounded sequence (x(n)) EN CRN converges. nЄN (e) If a sequence (xn)nEN C RN has a convergent subsequence, then (xn)nEN is convergent. [10 Marks] (ii) Give an example of a sequence (x(n))nEN CR2 which is located on the parabola x2 = x², contains infinitely many different points and converges to the limit x = (2,4). [5 Marks]arrow_forward2. (i) What does it mean to say that a sequence (x(n)) nEN CR2 converges to the limit x E R²? [1 Mark] (ii) Prove that if a set ECR2 is closed then every convergent sequence (x(n))nen in E has its limit in E, that is (x(n)) CE and x() x x = E. [5 Marks] (iii) which is located on the parabola x2 = = x x4, contains a subsequence that Give an example of an unbounded sequence (r(n)) nEN CR2 (2, 16) and such that x(i) converges to the limit x = (2, 16) and such that x(i) # x() for any i j. [4 Marksarrow_forward1. (i) which are not. Identify which of the following subsets of R2 are open and (a) A = (1, 3) x (1,2) (b) B = (1,3) x {1,2} (c) C = AUB (ii) Provide a sketch and a brief explanation to each of your answers. [6 Marks] Give an example of a bounded set in R2 which is not open. (iii) [2 Marks] Give an example of an open set in R2 which is not bounded. [2 Marks]arrow_forward
- 2. if limit. Recall that a sequence (x(n)) CR2 converges to the limit x = R² lim ||x(n)x|| = 0. 818 - (i) Prove that a convergent sequence (x(n)) has at most one [4 Marks] (ii) Give an example of a bounded sequence (x(n)) CR2 that has no limit and has accumulation points (1, 0) and (0, 1) [3 Marks] (iii) Give an example of a sequence (x(n))neN CR2 which is located on the hyperbola x2 1/x1, contains infinitely many different Total marks 10 points and converges to the limit x = (2, 1/2). [3 Marks]arrow_forward3. (i) Consider a mapping F: RN Rm. Explain in your own words the relationship between the existence of all partial derivatives of F and dif- ferentiability of F at a point x = RN. (ii) [3 Marks] Calculate the gradient of the following function f: R2 → R, f(x) = ||x||3, Total marks 10 where ||x|| = √√√x² + x/2. [7 Marks]arrow_forward1. (i) (ii) which are not. What does it mean to say that a set ECR2 is closed? [1 Mark] Identify which of the following subsets of R2 are closed and (a) A = [-1, 1] × (1, 3) (b) B = [-1, 1] x {1,3} (c) C = {(1/n², 1/n2) ER2 | n EN} Provide a sketch and a brief explanation to each of your answers. [6 Marks] (iii) Give an example of a closed set which does not have interior points. [3 Marks]arrow_forward
- A company specializing in lubrication products for vintage motors produce two blended oils, Smaza and Nefkov. They make a profit of K5,000.00 per litre of Smaza and K4,000.00 per litre of Nefkov. A litre of Smaza requires 0.4 litres of heavy oil and 0.6 litres of light oil. A litre of Nefkov requires 0.8 litres of heavy oil and 0.2 litres of light oil. The company has 100 litres of heavy oil and 80 litres of light oil. How many litres of each product should they make to maximize profits and what level of profit will they obtain? Show all your workings.arrow_forward1. Show that the vector field F(x, y, z) = (2x sin ye³)ix² cos yj + (3xe³ +5)k satisfies the necessary conditions for a conservative vector field, and find a potential function for F.arrow_forward1. Newton's Law of Gravitation (an example of an inverse square law) states that the magnitude of the gravitational force between two objects with masses m and M is |F| mMG |r|2 where r is the distance between the objects, and G is the gravitational constant. Assume that the object with mass M is located at the origin in R³. Then, the gravitational force field acting on the object at the point r = (x, y, z) is given by F(x, y, z) = mMG r3 r. mMG mMG Show that the scalar vector field f(x, y, z) = = is a potential function for r √√x² + y² . Fi.e. show that F = Vf. Remark: f is the negative of the physical potential energy, because F = -V(-ƒ).arrow_forward
- 2. Suppose f(x) = 3x² - 5x. Show all your work for the problems below.arrow_forwardwrite it down for better understanding pleasearrow_forward1. Suppose F(t) gives the temperature in degrees Fahrenheit t minutes after 1pm. With a complete sentence, interpret the equation F(10) 68. (Remember this means explaining the meaning of the equation without using any mathy vocabulary!) Include units. (3 points) =arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Correlation Vs Regression: Difference Between them with definition & Comparison Chart; Author: Key Differences;https://www.youtube.com/watch?v=Ou2QGSJVd0U;License: Standard YouTube License, CC-BY
Correlation and Regression: Concepts with Illustrative examples; Author: LEARN & APPLY : Lean and Six Sigma;https://www.youtube.com/watch?v=xTpHD5WLuoA;License: Standard YouTube License, CC-BY