
(a)
The value of
(a)
Answer to Problem 16E
The value of
Explanation of Solution
Given:
The matrices
Concept used:
Operations like addition and subtraction of matrices are only possible when they are of same dimension.
Dimension of matrix with a rows and b columns is given by
If a matrix is multiplied by a scalar then each element of the matrix is multiplied by the same scalar.
Calculation:
Add the matrix A and Bas follows:
Thus, the value of
Now, by graphing utility of matrix capability,
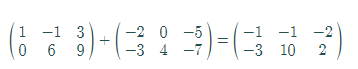
Hence, the result is verified.
(b)
The value of
(b)
Answer to Problem 16E
The value of
Explanation of Solution
Given:
The matrices
Concept used:
Operations like addition and subtraction of matrices are only possible when they are of same dimension.
Dimension of matrix with a rows and b columns is given by
If a matrix is multiplied by a scalar then each element of the matrix is multiplied by the same scalar.
Calculation:
Subtract the matrices A and Bas follows:
Thus, the value of
Now, by graphing utility of matrix capability,

Hence, the result is verified.
(c)
The value of
(c)
Answer to Problem 16E
The value of
Explanation of Solution
Given:
The matrix is
Concept used:
Operations like addition and subtraction of matrices are only possible when they are of same dimension.
Dimension of matrix with a rows and b columns is given by
If a matrix is multiplied by a scalar then each element of the matrix is multiplied by the same scalar.
Calculation:
Multiply all the elements of matrix A by 3 as follows:
Thus, the value of
Now, by graphing utility of matrix capability,
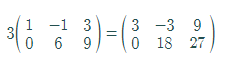
Hence, the result is verified.
(d)
The value of
(d)
Answer to Problem 16E
The value of
Explanation of Solution
Given:
The matrices
Concept used:
Operations like addition and subtraction of matrices are only possible when they are of same dimension.
Dimension of matrix with a rows and b columns is given by
If a matrix is multiplied by a scalar then each element of the matrix is multiplied by the same scalar.
Calculation:
The value of
Thus, the value of
Now, by graphing utility of matrix capability,
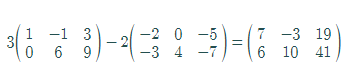
Hence, the result is verified.
Chapter 7 Solutions
Precalculus with Limits: A Graphing Approach
- Use 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forwarduse Cauchy Mean-Value Theorem to derive Corollary 12.6.2, and then derive 12.6.3arrow_forwardExplain the focus and reasons for establishment of 12.5.4arrow_forward
- Explain the focus and reasons for establishment of 12.5.3 about alternating series. and explain the reason why (sigma k=1 to infinite)(-1)k+1/k = 1/1 - 1/2 + 1/3 - 1/4 + .... converges.arrow_forwardExplain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forwardUse identity (1+x+x2+...+xn)*(1-x)=1-xn+1 to derive the result of 12.2.2. Please notice that identity doesn't work when x=1.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





