Chapter 7.3, Problem 6SP

Landing Vehicle

NASA is planning a mission to Mars. To save money, engineers have decided to adapt one of the moon landing vehicles for the new mission. However, they are concerned about how the different gravitational forces will affect the suspension system that cushions the craft when it touches down. The acceleration resulting from gravity on the moon is 1.6 m/sec², whereas on Mars it is 3.7 m/sec².

The suspension system on the craft can be modeled as a damped spring mass system. In this case, the spring is below the moon lander, so the spring is slightly compressed at equilibrium, as shown in Figure 7.12.

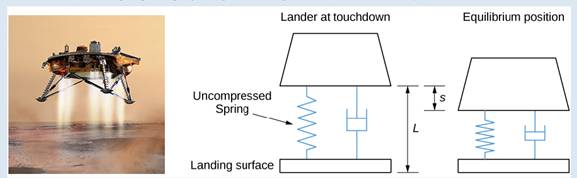
Figure 7.12 The landing craft suspension can be represented as a damped spring-mass system. (credit “lander": NASA)

We retain the convention that down is positive. Despite the new orientation, an examination of the forces affecting the lander shows that the same differential equation can be used to model the position of the landing craft relative to equilibrium:

   $m{x}^{″}+b{x}^{\prime }+kx=0$ ,

where m is the mass of the lander, b is the damping coef?cient, and k is the spring constant.

6. What adjustments, if any, should the NASA engineers make to use the lander safely on Mars?