MyLab Math with Pearson eText -- 24-Month Standalone Access Card -- For Differential Equations and Boundary Value Problems: Computing and Modeling Tech Update
5th Edition
ISBN: 9780134872971
Author: Edwards, C., Penney, David, Calvis
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 7.3, Problem 40P
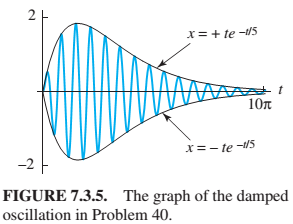
Problems 39 and 40 illustrate Iwo types of resonance in a mass-spring-dashpot system with given external force F(t) and with the initial conditions
Suppose that m = 1, k = 9.04, c = 0.4, and
Show that the maximum value of the amplitude function
Fig. 7.3.5) the oscillations of the mass increase in amplitude during the first s before being damped out as
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A beam containing 1000 monoenergetic photons applied to material with a thickness of 0.5cm and
linear attenuation coefficient of 82 x 1 m-1. Find the number of outgoing beam.
1) Given the sinusoidal voltage v(t)
50 cos(30t + 10°) V, find: (a) the amplitude Vm, (b) the period T,
(c) the frequency f, and (d) v(t) at t= 10 ms.
In the Bohr model of the hydrogen atom, an electron in the 4th excited state moves at a speed of 1.37 x 105 m/s in a circular path of radius
8.46 x 1010 m. What is the effective current associated with this orbiting electron?
4.12373E3
Your response differs significantly from the correct answer. Rework your solution from the beginning and check each step carefully. mA
Chapter 7 Solutions
MyLab Math with Pearson eText -- 24-Month Standalone Access Card -- For Differential Equations and Boundary Value Problems: Computing and Modeling Tech Update
Ch. 7.1 - Apply the definition in (1) to find directly tile...Ch. 7.1 - Prob. 2PCh. 7.1 - Prob. 3PCh. 7.1 - Prob. 4PCh. 7.1 - Prob. 5PCh. 7.1 - Prob. 6PCh. 7.1 - Prob. 7PCh. 7.1 - Prob. 8PCh. 7.1 - Prob. 9PCh. 7.1 - Prob. 10P
Ch. 7.1 - Prob. 11PCh. 7.1 - Prob. 12PCh. 7.1 - Prob. 13PCh. 7.1 - Prob. 14PCh. 7.1 - Prob. 15PCh. 7.1 - Prob. 16PCh. 7.1 - Prob. 17PCh. 7.1 - Prob. 18PCh. 7.1 - Prob. 19PCh. 7.1 - Prob. 20PCh. 7.1 - Prob. 21PCh. 7.1 - Prob. 22PCh. 7.1 - Prob. 23PCh. 7.1 - Prob. 24PCh. 7.1 - Prob. 25PCh. 7.1 - Prob. 26PCh. 7.1 - Prob. 27PCh. 7.1 - Prob. 28PCh. 7.1 - Prob. 29PCh. 7.1 - Prob. 30PCh. 7.1 - Prob. 31PCh. 7.1 - Prob. 32PCh. 7.1 - Prob. 33PCh. 7.1 - Prob. 34PCh. 7.1 - Prob. 35PCh. 7.1 - Prob. 36PCh. 7.1 - Given a0, let f(t)=1 if 0__1a,f(t)=0 if t__a....Ch. 7.1 - Given that 0ab. Let f(t)=1 if a__tb,f(t)=0 if...Ch. 7.1 - Prob. 39PCh. 7.1 - Prob. 40PCh. 7.1 - Prob. 41PCh. 7.1 - Given constants a and b. define h(t) for t__0 by...Ch. 7.2 - Prob. 1PCh. 7.2 - Prob. 2PCh. 7.2 - Prob. 3PCh. 7.2 - Prob. 4PCh. 7.2 - Prob. 5PCh. 7.2 - Prob. 6PCh. 7.2 - Prob. 7PCh. 7.2 - Prob. 8PCh. 7.2 - Prob. 9PCh. 7.2 - Prob. 10PCh. 7.2 - Prob. 11PCh. 7.2 - Prob. 12PCh. 7.2 - Prob. 13PCh. 7.2 - Prob. 14PCh. 7.2 - Prob. 15PCh. 7.2 - Prob. 16PCh. 7.2 - Prob. 17PCh. 7.2 - Prob. 18PCh. 7.2 - Prob. 19PCh. 7.2 - Prob. 20PCh. 7.2 - Prob. 21PCh. 7.2 - Prob. 22PCh. 7.2 - Prob. 23PCh. 7.2 - Prob. 24PCh. 7.2 - Prob. 25PCh. 7.2 - Prob. 26PCh. 7.2 - Prob. 27PCh. 7.2 - Prob. 28PCh. 7.2 - Prob. 29PCh. 7.2 - Prob. 30PCh. 7.2 - Prob. 31PCh. 7.2 - Prob. 32PCh. 7.2 - Prob. 33PCh. 7.2 - Prob. 34PCh. 7.2 - Prob. 35PCh. 7.2 - Prob. 36PCh. 7.2 - Prob. 37PCh. 7.3 - Prob. 1PCh. 7.3 - Prob. 2PCh. 7.3 - Prob. 3PCh. 7.3 - Prob. 4PCh. 7.3 - Prob. 5PCh. 7.3 - Prob. 6PCh. 7.3 - Prob. 7PCh. 7.3 - Prob. 8PCh. 7.3 - Prob. 9PCh. 7.3 - Prob. 10PCh. 7.3 - Prob. 11PCh. 7.3 - Prob. 12PCh. 7.3 - Prob. 13PCh. 7.3 - Prob. 14PCh. 7.3 - Prob. 15PCh. 7.3 - Prob. 16PCh. 7.3 - Prob. 17PCh. 7.3 - Prob. 18PCh. 7.3 - Prob. 19PCh. 7.3 - Prob. 20PCh. 7.3 - Prob. 21PCh. 7.3 - Prob. 22PCh. 7.3 - Prob. 23PCh. 7.3 - Prob. 24PCh. 7.3 - Prob. 25PCh. 7.3 - Prob. 26PCh. 7.3 - Prob. 27PCh. 7.3 - Prob. 28PCh. 7.3 - Prob. 29PCh. 7.3 - Prob. 30PCh. 7.3 - Prob. 31PCh. 7.3 - Prob. 32PCh. 7.3 - Prob. 33PCh. 7.3 - Prob. 34PCh. 7.3 - Prob. 35PCh. 7.3 - Prob. 36PCh. 7.3 - Prob. 37PCh. 7.3 - Prob. 38PCh. 7.3 - Problems 39 and 40 illustrate Iwo types of...Ch. 7.3 - Problems 39 and 40 illustrate Iwo types of...Ch. 7.4 - Find the convolution f(t)g(t) in Problems 1...Ch. 7.4 - Prob. 2PCh. 7.4 - Prob. 3PCh. 7.4 - Prob. 4PCh. 7.4 - Prob. 5PCh. 7.4 - Prob. 6PCh. 7.4 - Prob. 7PCh. 7.4 - Prob. 8PCh. 7.4 - Prob. 9PCh. 7.4 - Prob. 10PCh. 7.4 - Prob. 11PCh. 7.4 - Prob. 12PCh. 7.4 - Prob. 13PCh. 7.4 - Prob. 14PCh. 7.4 - Prob. 15PCh. 7.4 - Prob. 16PCh. 7.4 - Prob. 17PCh. 7.4 - Prob. 18PCh. 7.4 - Prob. 19PCh. 7.4 - Prob. 20PCh. 7.4 - Prob. 21PCh. 7.4 - Prob. 22PCh. 7.4 - Prob. 23PCh. 7.4 - Prob. 24PCh. 7.4 - Prob. 25PCh. 7.4 - Prob. 26PCh. 7.4 - Prob. 27PCh. 7.4 - Prob. 28PCh. 7.4 - Prob. 29PCh. 7.4 - Prob. 30PCh. 7.4 - Prob. 31PCh. 7.4 - Prob. 32PCh. 7.4 - Prob. 33PCh. 7.4 - Prob. 34PCh. 7.4 - Prob. 35PCh. 7.4 - Prob. 36PCh. 7.4 - Prob. 37PCh. 7.4 - Prob. 38PCh. 7.4 - Prob. 39PCh. 7.4 - Prob. 40PCh. 7.4 - Prob. 41PCh. 7.5 - Prob. 1PCh. 7.5 - Prob. 2PCh. 7.5 - Prob. 3PCh. 7.5 - Prob. 4PCh. 7.5 - Prob. 5PCh. 7.5 - Prob. 6PCh. 7.5 - Prob. 7PCh. 7.5 - Prob. 8PCh. 7.5 - Prob. 9PCh. 7.5 - Prob. 10PCh. 7.5 - Prob. 11PCh. 7.5 - Prob. 12PCh. 7.5 - Prob. 13PCh. 7.5 - Prob. 14PCh. 7.5 - Prob. 15PCh. 7.5 - Prob. 16PCh. 7.5 - Prob. 17PCh. 7.5 - Prob. 18PCh. 7.5 - Prob. 19PCh. 7.5 - Prob. 20PCh. 7.5 - Prob. 21PCh. 7.5 - Prob. 22PCh. 7.5 - Prob. 23PCh. 7.5 - Prob. 24PCh. 7.5 - Prob. 25PCh. 7.5 - Prob. 26PCh. 7.5 - Let g(t) be the staircase function of Fig. 7.5.15....Ch. 7.5 - Suppose that f(i) is a periodic function of period...Ch. 7.5 - Suppose that f(t) is the half-wave rectification...Ch. 7.5 - Let g(t)=u(tk)f(tk), where f(t) is the function of...Ch. 7.5 - Prob. 31PCh. 7.5 - Prob. 32PCh. 7.5 - Prob. 33PCh. 7.5 - Prob. 34PCh. 7.5 - Prob. 35PCh. 7.5 - Prob. 36PCh. 7.5 - Prob. 37PCh. 7.5 - Prob. 38PCh. 7.5 - Prob. 39PCh. 7.5 - Prob. 40PCh. 7.5 - Prob. 41PCh. 7.5 - Prob. 42PCh. 7.6 - Prob. 1PCh. 7.6 - Prob. 2PCh. 7.6 - Prob. 3PCh. 7.6 - Prob. 4PCh. 7.6 - Prob. 5PCh. 7.6 - Prob. 6PCh. 7.6 - Prob. 7PCh. 7.6 - Prob. 8PCh. 7.6 - Prob. 9PCh. 7.6 - Prob. 10PCh. 7.6 - Prob. 11PCh. 7.6 - Prob. 12PCh. 7.6 - Prob. 13PCh. 7.6 - Prob. 14PCh. 7.6 - This problem deals with a mass in on a spring...Ch. 7.6 - Prob. 16PCh. 7.6 - Prob. 17PCh. 7.6 - Prob. 18PCh. 7.6 - Prob. 19PCh. 7.6 - Repeat Problem 19, except suppose that the switch...Ch. 7.6 - Prob. 21PCh. 7.6 - Prob. 22P
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
What is the general problem with static scoping?
Concepts Of Programming Languages
This optional Google account security feature sends you a message with a code that you must enter, in addition ...
SURVEY OF OPERATING SYSTEMS
What output would the code in the previous question produce if we changed 46 in the first statement to 12?
Java: An Introduction to Problem Solving and Programming (8th Edition)
(Factorials) Factorials are used frequently in probability problems. The factorial of a positive integer n (wri...
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
Find the no-load value of υo in the circuit shown.
Find υo when RL is 150 Ω.
How much power is dissipated in th...
Electric Circuits. (11th Edition)
T F Variable names may begin with a number.
Starting Out with C++ from Control Structures to Objects (9th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- PROBLEM 24 - 0589: A forced oscillator is a system whose behavior can be described by a second-order linear differential equation of the form: ÿ + Ajý + A2y (t) = (1) where A1, A2 are positive %3D E(t) constants and E(t) is an external forcing input. An automobile suspension system, with the road as a vertical forcing input, is a forced oscillator, for example, as shown in Figure #1. Another example is an RLC circuit connected in series with an electromotive force generator E(t), as shown in Figure #2. Given the initial conditions y(0) = Yo and y(0) = zo , write a %3D FORTRAN program that uses the modified Euler method to simulate this system from t = 0 to t = tf if: Case 1: E(t) = h whereh is %3D constant Case 2: E(t) is a pulse of height h and width (t2 - t1) . Case 3: E(t) is a sinusoid of amplitude A, period 2n/w and phase angle p . E(t) is a pulse train Case 4: with height h, width W, period pW and beginning at time t =arrow_forwardProblem (1) For the circuit shown in fig. find the current supplied by the battery by using delta/star transformation 400 www 2002 500 30 V 2002 www 30Ω www 5Ω wwarrow_forwardAns [3.43A , 0.506 , 2.12A , 0.942] Q16/ The star-connected rotor of a 3-phase induction motor has a resistance and standstill reactance 0.4 Q/phase respectively. The e.m.f. induced between the slip rings at standstill is 80V, the stator being connected to a normal supply voltage. Find the rotor current and power factor at starting when the rings are (i) short-circuited (ii) joined to star-connected Ans [18.25A , 0.16,7.76 , 0.91] resistance of 52/phase.arrow_forward
- Determine the transfer function, of the rotational mechanical system shown in T(s) Figure Q2. The variables 6,(t) and 02(t) refer to angular displacement of motion, while T(t) is a torque applied to the system. Given the value of spring, damping coefficient and inertia as; J: 5 kg-m? Di: 5 N-m-s/rad J2: 10 kg-m? K : 6 N-m/rad K2 : 5 N-m/rad D::4 N-m-s/rad D3:2 N-m-s/rad T(t) e,(1) D2 K2 0000 D1 D3 Figure Q2arrow_forward1. A. If the junction depth of Phosphorous atoms diffused into a p-type wafer after a 1.25 hours pre-deposition stage is 6.575 µm, determine the diffusivity of the dopants at 1300 °C, in cm²/s. Assume that the solubility of P to the wafer is 5.875 X 1020 /cm³ and that the bulk concentration of the dopants is 6.745 X 1015 /cm³. (4 points) B. If the dopants were driven into the substrate for 2.2 hours, at the same temperature, what would be the junction depth in um, after the drive-in process? (6 points)arrow_forwardPROBLEM 24 - 0586: A free harmonic oscillator (FHO) is a system whose behavior can be described by a second- order, linear differential equation of the form: = -Ay(t) (1) where A is a positive constant. Two FHO systems are a spring-mass system and an LC electric circuit: Y=dy/dt y(t) Spring- x- FHO V displacement =velocit q-charge in coulombs mass LC i circuit =curren in ampere Given the initial conditions y(0) = %3D Yo and y(0) = Zo , write a FORTRAN program that uses the modified Euler method to simulate this system from t = 0 to t %3D = tf . LINEAR SPRING OF STIFFNESS K C INDUCTOR CAPACITOR (HENRYS) 1 IM MASS (FARADS)arrow_forward
- We wish to coat a glass surface with an appropriate dielectric layer to provide total transmission from air to the glass at a free-space wavelength of 570 nm. The glass has refractive index n3 = 1.45. Determine the required index for the coating and its minimum thicknessarrow_forward3. You have seen how Kirchhoff's laws were used in your lectures to obtain a 2nd order differential equation where we solved for the current. This time we will use an even simpler concept: principle of conservation of energy to derive the 2nd order differential equation where we will solve for the charge. Take a look at the circuit below. IHE 2F In the circuit above, we have a capacitor with capacitance 2 F, an inductor of inductance 5 H and a resistor of 32 (a) The total energy that is supplied to the resistor is LI? E = 2 Q? 20 where L is the inductance, I is the current, C is the capacitance and Q is the charge. Write down the total energy supplied E in terms of Q and t only. OP Remember that I = dt (b) Now you know that the power dissipation through a resistor is -1R. Use the conservation of energy (energy gain rate = energy loss rate) to derive the differential equation in terms Q and t only. (c) Solve the differential equation for initial charge to be Qo with a initial current of…arrow_forward21...arrow_forward
- Questionarrow_forwardHelp me to solve this Find the equation for a sine wave signal with a frequency of 10 Hz, maximum amplitude of 20 volts, and phase angle of 0arrow_forwardLogic Function F (x, y, z, w) = ∑ m (0,2,4,6,10,13) + ∑ k (8,12) as sum of minimers are given. (Note: There are terms that are not taken into account.) a. Obtain the Truth Table. b. Simplify with the Karnough Map approach. c. Draw the simplified Logic circuit with two input AND-NOT (NAND) gates. With how many apples you realized, what is your gain? Comment.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
C++ for Engineers and Scientists
Computer Science
ISBN:9781133187844
Author:Bronson, Gary J.
Publisher:Course Technology Ptr
Boolean Algebra - Digital Logic and Logic Families - Industrial Electronics; Author: Ekeeda;https://www.youtube.com/watch?v=u7XnJos-_Hs;License: Standard YouTube License, CC-BY
Boolean Algebra 1 – The Laws of Boolean Algebra; Author: Computer Science;https://www.youtube.com/watch?v=EPJf4owqwdA;License: Standard Youtube License