Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 73, Problem 37AR
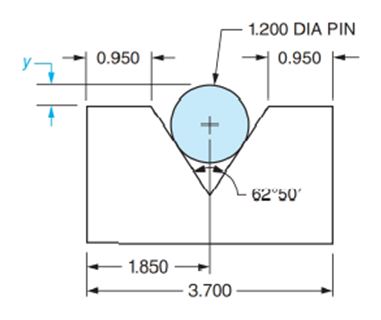
Solve the following applied right triangle exercises. Compute linear values to 3 decimal places, customary unit angles to the nearer minute, and metric angles to the nearer hundredth degree.
Determine check dimension y.
All dimensions are in inches.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Sara (a 23 year old college graduate) is starting her first career. She met with a financial planner and has determined that she wants $1,000,000 when she retires at the age of 63. She has found an annuity that pays 4.25%, compounded quarterly.
What will she need to save each month, if Sara waits 20 years to start saving?
N:
P/Y:
I%:
C/Y:
PMT:
FV:
End or Begin
$4158.98
$4,115.26
$2645.83
$6,707.40
Sara (a 23 year old college graduate) is starting her first career. She met with a financial planner and has determined that she wants $1,000,000 when she retires at the age of 63. She has found an annuity that pays 4.25%, compounded quarterly.
What will she need to save each month, if
a) Sara begins saving now?
N:
P/Y:
I%:
C/Y:
PMT:
FV:
End or Begin
$1,323.80
$1,376.59
$794.74
$1,000,000
The entire graph of the function g is shown in the figure below.
Write the domain and range of g as intervals or unions of intervals.
5
4
-3.
2
3
omain =
range ☐
=
Chapter 73 Solutions
Mathematics For Machine Technology
Ch. 73 - With reference 1, name the sides of each of the...Ch. 73 - With reference to 1, name the sides of each of the...Ch. 73 - Prob. 3ARCh. 73 - Prob. 4ARCh. 73 - Prob. 5ARCh. 73 - Prob. 6ARCh. 73 - Prob. 7ARCh. 73 - Prob. 8ARCh. 73 - Prob. 9ARCh. 73 - Prob. 10AR
Ch. 73 - Prob. 11ARCh. 73 - Prob. 12ARCh. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in decimal degree to 2...Ch. 73 - Determine the values A in decimal degree to 2...Ch. 73 - Determine the values A in decimal degree to 2...Ch. 73 - For each of the following functions of angles,...Ch. 73 - For each of the following functions of angles,...Ch. 73 - For each of the following functions of angles,...Ch. 73 - For each of the following functions of angles,...Ch. 73 - Solve the following exercises. Compute angles to...Ch. 73 - Solve the following exercises. Compute angles to...Ch. 73 - Solve the following exercises. Compute angles to...Ch. 73 - Prob. 29ARCh. 73 - Prob. 30ARCh. 73 - Prob. 31ARCh. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Prob. 40ARCh. 73 - Prob. 41ARCh. 73 - Prob. 42ARCh. 73 - Prob. 43ARCh. 73 - Prob. 44ARCh. 73 - Prob. 45ARCh. 73 - Prob. 46ARCh. 73 - Prob. 47ARCh. 73 - Prob. 48ARCh. 73 - Prob. 49ARCh. 73 - Determine the sine, cosine, tangent, cotangent,...Ch. 73 - Determine the sine, cosine, tangent, cotangent,...Ch. 73 - Prob. 52ARCh. 73 - Prob. 53ARCh. 73 - Determine the sine, cosine, tangent, cotangent,...Ch. 73 - Prob. 55ARCh. 73 - Prob. 56AR
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Can you prove this integral equation?Note: It also has an application to prove that 22/7 > π.arrow_forward1. The number of claims is modelled by a NB2(n, p) (the number of fail- ures before the nth success with probability p of success). The sample x = (x1, x2,,XN) with N = 100 returns N N xj = 754, Σε = 70425. j=1 Estimate the parameters n and p using the point estimates. [5 Marks]arrow_forwardf(x) = x + 1; x(x) = x − 2. Solve the equation for x : |f(x)+4(x)| = |f(x)|+|4(x)|. 00arrow_forward
- y = log 5 – x2 - 4 00arrow_forwardPlease fill in the rest of the steps of the proof of Thm 2.5. Show how "Repeating this step with n-1,n-2,...,2 in place of n" gives us the desired result.arrow_forwardConsider the initial value problem y"+y'-12y= 0, y(0) = a, y'(0) = 4 Find the value of a so that the solution to the initial value problem approaches zero as too a =arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill 
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Trigonometric Ratios; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9-eHMMpQC2k;License: Standard YouTube License, CC-BY