Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 73, Problem 54AR
Determine the sine, cosine, tangent, cotangent, secant, and cosecant of each of the following angles.
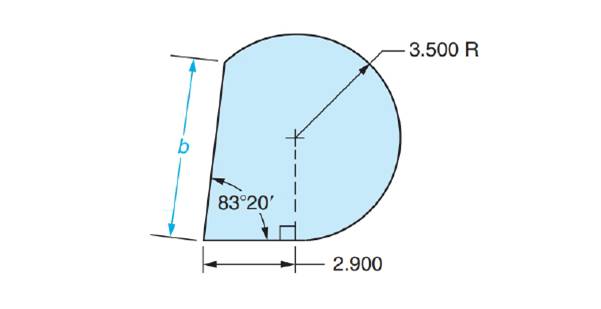
A piece of stock is to be machined as shown.
Determine dimension b.
All dimensions are in inches.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
This is advanced mathematics question that need detailed solutions
Question:
Let F be a field. Prove that F contains a unique smallest subfield, called the prime subfield, which is
isomorphic to either Q or Zp for some prime p.
Instructions:
•
Begin by identifying the identity element 1 € F.
•
Use the closure under addition and inverses to build a subring.
•
•
•
Show that either the map ZF or Q →F is an embedding.
Prove minimality and uniqueness.
Discuss the characteristic of a field and link it to the structure of the prime subfield.
Topic: Group Theory | Abstract Algebra
Question:
Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe
the number of Sylow subgroups for each.
Instructions:
•
Use Sylow's Theorems (existence, conjugacy, and counting).
•
List divisors of 45 and compute possibilities for n for p = 3 and p = 5.
Show that if n = 1, the subgroup is normal.
Conclude about group structure using your analysis.
Chapter 73 Solutions
Mathematics For Machine Technology
Ch. 73 - With reference 1, name the sides of each of the...Ch. 73 - With reference to 1, name the sides of each of the...Ch. 73 - Prob. 3ARCh. 73 - Prob. 4ARCh. 73 - Prob. 5ARCh. 73 - Prob. 6ARCh. 73 - Prob. 7ARCh. 73 - Prob. 8ARCh. 73 - Prob. 9ARCh. 73 - Prob. 10AR
Ch. 73 - Prob. 11ARCh. 73 - Prob. 12ARCh. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in degrees and minutes that...Ch. 73 - Determine the values A in decimal degree to 2...Ch. 73 - Determine the values A in decimal degree to 2...Ch. 73 - Determine the values A in decimal degree to 2...Ch. 73 - For each of the following functions of angles,...Ch. 73 - For each of the following functions of angles,...Ch. 73 - For each of the following functions of angles,...Ch. 73 - For each of the following functions of angles,...Ch. 73 - Solve the following exercises. Compute angles to...Ch. 73 - Solve the following exercises. Compute angles to...Ch. 73 - Solve the following exercises. Compute angles to...Ch. 73 - Prob. 29ARCh. 73 - Prob. 30ARCh. 73 - Prob. 31ARCh. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Solve the following applied right triangle...Ch. 73 - Prob. 40ARCh. 73 - Prob. 41ARCh. 73 - Prob. 42ARCh. 73 - Prob. 43ARCh. 73 - Prob. 44ARCh. 73 - Prob. 45ARCh. 73 - Prob. 46ARCh. 73 - Prob. 47ARCh. 73 - Prob. 48ARCh. 73 - Prob. 49ARCh. 73 - Determine the sine, cosine, tangent, cotangent,...Ch. 73 - Determine the sine, cosine, tangent, cotangent,...Ch. 73 - Prob. 52ARCh. 73 - Prob. 53ARCh. 73 - Determine the sine, cosine, tangent, cotangent,...Ch. 73 - Prob. 55ARCh. 73 - Prob. 56AR
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Topic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardComplete solution requiredarrow_forward
- Topic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardDo with graph of the regionarrow_forward
- Problem 9: The 30-kg pipe is supported at A by a system of five cords. Determine the force in each cord for equilibrium. B 60º A E Harrow_forwardd((x, y), (z, w)) = |xz|+|yw|, show that whether d is a metric on R² or not?. Q3/Let R be a set of real number and d: R² x R² → R such that -> d((x, y), (z, w)) = max{\x - zl, ly - w} show that whether d is a metric on R² or not?. Q4/Let X be a nonempty set and d₁, d₂: XXR are metrics on X let d3,d4, d5: XX → R such that d3(x, y) = 4d2(x, y) d4(x, y) = 3d₁(x, y) +2d2(x, y) d5(x,y) = 2d₁ (x,y))/ 1+ 2d₂(x, y). Show that whether d3, d4 and d5 are metric on X or not?arrow_forwardJu at © Ju 370 = x (- пье zxp = c² (2² 4 ) dx² ахе 2 nze dyz t nzp Q/what type of partial differential equation (PDE) are the following-arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning 
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Fundamental Trigonometric Identities: Reciprocal, Quotient, and Pythagorean Identities; Author: Mathispower4u;https://www.youtube.com/watch?v=OmJ5fxyXrfg;License: Standard YouTube License, CC-BY