
Concept explainers
Use the Collocation Method with
a.
b.
Plot the approximate solutions together with the exact solutions (a)
a.
To find: Approximate solution for linear boundary value problem by collocation method.
Explanation of Solution
% Program for Finite element solution of linear BVP % Inputs are interval inter, boundary values bv, number of steps n % Output: solution values c function c=bvpfem(inter,bv,n) a=inter(1);b=inter(2);ya=bv(1);yb=bv(2); h=(b-a)/(n+1); alpha=(8/3)*h+2/h; beta = (2/3)*h-1/h; e=ones(n,1); M=spdiags([beta*e alpha*e beta*e],-1:1,n,n); d=zeros(n,1); d(1)= -ya*beta; d(n)= -yb*beta; c=M\d; c= bvpfem([0 1],[0 0.33e],8);
Collocation is applied
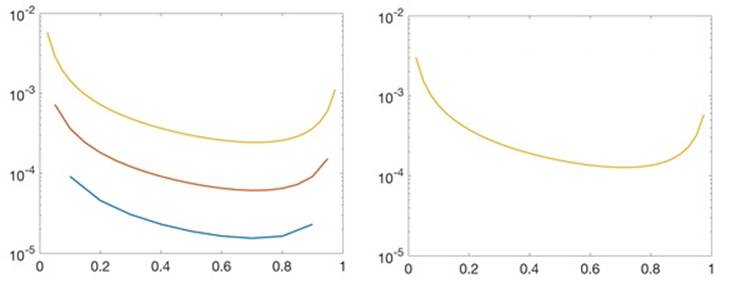
b.
To find: Approximate solution for linear boundary value problem by collocation method.
Explanation of Solution
% Program for Finite element solution of linear BVP % Inputs are interval inter, boundary values bv, number of steps n % Output: solution values c function c=bvpfem(inter,bv,n) a=inter(1);b=inter(2);ya=bv(1);yb=bv(2); h=(b-a)/(n+1); alpha=(8/3)*h+2/h; beta = (2)*h-4/h; e=ones(n,1); M=spdiags([beta*e alpha*e beta*e],-1:1,n,n); d=zeros(n,1); d(1)= -ya*beta; d(n)= -yb*beta; c=M\d; c= bvpfem([0 1],[1 e],16);
Similar to (a). The first and last equations are c1=1and c1+…+cn=e. The remaining n-2equations are
Substituting
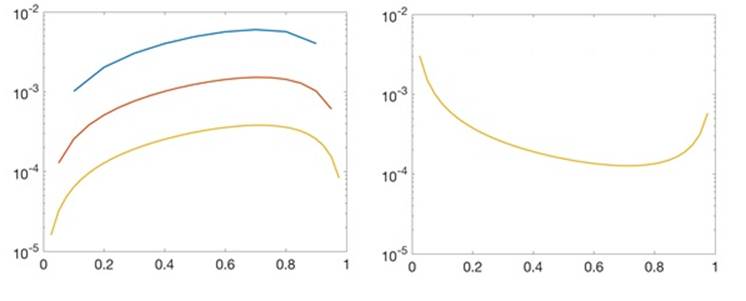
Want to see more full solutions like this?
Chapter 7 Solutions
Numerical Analysis
Additional Math Textbook Solutions
Pathways To Math Literacy (looseleaf)
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
College Algebra (7th Edition)
Probability And Statistical Inference (10th Edition)
Elementary Statistics: A Step By Step Approach
Elementary Statistics: Picturing the World (7th Edition)
- 3. A different 7-Eleven has a bank of slurpee fountain heads. Their available flavors are as follows: Mountain Dew, Mountain Dew Code Red, Grape, Pepsi and Mountain Dew Livewire. You fill five different cups full with each type of flavor. How many different ways can you arrange the cups in a line if exactly two Mountain Dew flavors are next to each other? 3.2.1arrow_forwardBusinessarrow_forwardWhat is the area of this figure? 5 mm 4 mm 3 mm square millimeters 11 mm Submit 8 mm Work it out 9 mmarrow_forward
- No chatgpt pls will upvotearrow_forwardFind all solutions of the polynomial congruence x²+4x+1 = 0 (mod 143). (The solutions of the congruence x² + 4x+1=0 (mod 11) are x = 3,4 (mod 11) and the solutions of the congruence x² +4x+1 = 0 (mod 13) are x = 2,7 (mod 13).)arrow_forwardhttps://www.hawkeslearning.com/Statistics/dbs2/datasets.htmlarrow_forward
- Determine whether each function is an injection and determine whether each is a surjection.The notation Z_(n) refers to the set {0,1,2,...,n-1}. For example, Z_(4)={0,1,2,3}. f: Z_(6) -> Z_(6) defined by f(x)=x^(2)+4(mod6). g: Z_(5) -> Z_(5) defined by g(x)=x^(2)-11(mod5). h: Z*Z -> Z defined by h(x,y)=x+2y. j: R-{3} -> R defined by j(x)=(4x)/(x-3).arrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.arrow_forwardLet A = {a, b, c, d}, B = {a,b,c}, and C = {s, t, u,v}. Draw an arrow diagram of a function for each of the following descriptions. If no such function exists, briefly explain why. (a) A function f : AC whose range is the set C. (b) A function g: BC whose range is the set C. (c) A function g: BC that is injective. (d) A function j : A → C that is not bijective.arrow_forward
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
