Chapter 7.2, Problem 49E

a.

To determine

To calculate: To find the system of equations such that one equation represents the total amount of the final mixture required and the other represents the percent of acid in the final mixture.

Answer to Problem 49E

  $\begin{array}{l}x+y=30\\ 0.25x+0.5y=12\end{array}$

Explanation of Solution

Given information:

Given that thirty liters of a 40% acid solution is obtained by mixing a 25 % solution with a 50% solution.

Calculation: 

Let x and y represent the amounts of the 25% and 50% solutions respectively used to make the 40% solution.

So the total amount of solution is given by:

  $x+y=30$

Amount of acid in x liters of 25% solution is given by:

  $\frac{25}{100}\times x=0.25x$

Similarly amount of acid in y liters of 50% solution is given by:

  $\frac{50}{100}\times y=0.5y$

Also the amount of acid in 30 liters of 40% solution is given by:

  $\frac{40}{100}\times 30=12$

Hence the amount of acid in final solution is represented by the equation:

  $0.25x+0.5y=12$

Therefore the required equations representing the given system are:

  $\begin{array}{l}x+y=30\\ 0.25x+0.5y=12\end{array}$

b.

To determine

To graph: To plot the two equations on the same graph and check how amount of 50% solution changes as amount of 25% solution changes.

Explanation of Solution

Given information: 

Given that thirty liters of a 40% acid solution is obtained by mixing a 25 % solution with a 50% solution.

x and y represent the amounts of the 25% and 50% solutions respectively used to make the 40% solution.

The equations are:

  $\begin{array}{l}x+y=30\\ 0.25x+0.5y=12\end{array}$

Graph: 

Plotting the equations on a graph with x and y as the axes:

  

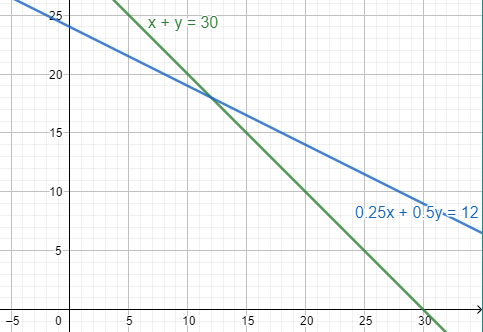
Interpretation: 

From the graph it is seen that in both the cases i.e. for both the equations as x increasesy decreases.

Hence, the amount of 50% solution decreases as amount of 25% solution changes.

c.

To determine

To calculate: To find the quantity of each solution required to obtain the final mixture.

Answer to Problem 49E

  $x=12,y=18$

Explanation of Solution

Given information:

Given that thirty liters of a 40% acid solution is obtained by mixing a 25 % solution with a 50% solution.

Calculation: 

From the graph it is seen that both the lines meet at a point where

  $x=12,y=18$

Therefore the quantities of the solutions required are:

  $x=12,y=18$

i.e. 12 liters of 25% solutions and 18 liters of 50% solution