Chapter 7.2, Problem 26E

To determine

The solution of the system of equations by using elimination method and check the solution graphically.

Answer to Problem 26E

  $\left(\frac{90}{31},\frac{-67}{31}\right)$ .

Explanation of Solution

Given information:

The system of the equation are:

  $\{\begin{array}{l}0.05x-0.03y=0.21\\ 0.07x+0.02y=0.16\end{array}$

Calculation:

The given equations are $\{\begin{array}{l}0.05x-0.03y=0.21\\ 0.07x+0.02y=0.16\end{array}$ .

To find the solution of the system of equation by elimination method, firstly multiply the both equation by $100$ :

  $\begin{array}{l}5x-3y=21\\ 7x+2y=16\end{array}$

Now multiply the first equation by $7$ and the second equation by $5$ :

  $\begin{array}{l}35x-21y=147\\ 35x+10y=80\end{array}$

Subtract the above equation one from another:

  $\begin{array}{l}\underset{\_}{\begin{array}{l}35x-21y=147\\ 35x+10y=80\\ ---\end{array}}\\ \text{ -31}y=67\\ y=-\frac{67}{31}\end{array}$

Substitute the value of $y=-\frac{67}{31}$ in the given first equation to find the value of $x$ :

  $\begin{array}{l}0.05x-0.03y=0.21\\ 0.05x-0.03\left(-\frac{67}{31}\right)=0.21\\ 0.05x+\frac{2.01}{31}=0.21\\ x=\frac{90}{31}\end{array}$

The values of $x$ and $y$ are $\frac{90}{31}$ and $\frac{-67}{31}$ .

Now, verify the given equation by graphically are as shown below:

  

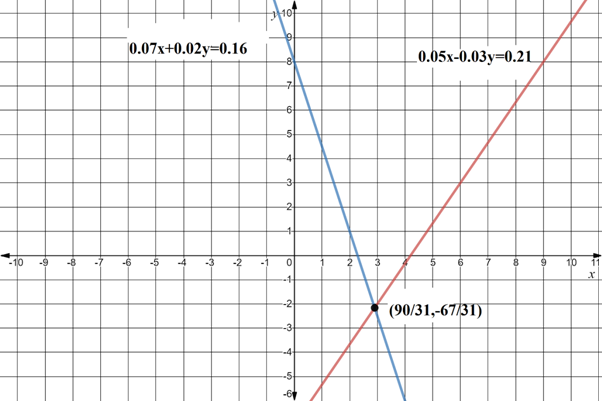
The lines are intersected at $\left(\frac{90}{31},\frac{-67}{31}\right)$ so, we will verify the solution of the system of equation by substituting the point of intersection as follows:

  $\begin{array}{l}0.07x+0.02y=0.16\\ 0.07(\frac{90}{31})+0.02(\frac{-67}{31})=0.16\\ 0.16=0.16\end{array}$ $\begin{array}{l}0.05x-0.03y=0.21\\ 0.05(\frac{90}{31})-0.03(\frac{-67}{31})=0.21\\ 0.21=0.21\end{array}$

It mean point of intersection satisfies both the equation and hence it will be the solution of the system of equations.

Thus,the solutions are $\left(\frac{90}{31},\frac{-67}{31}\right)$ .