
Concept explainers
a.
The percentage of students surveyed who prefer summer; fall.
a.
Answer to Problem 22E
Percent of students surveyed who prefer summer =
Percent of students surveyed who prefer fall =
Explanation of Solution
Given:
Middle schools students are surveyed to know their preference of season for holding school trip.
The bar graph given in the question:
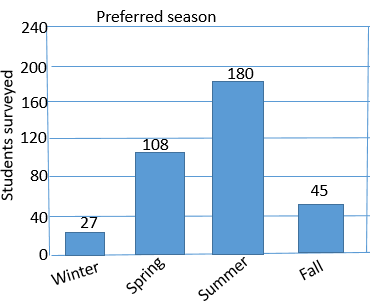
Calculation:
As per the problem
Consider the bar graph,
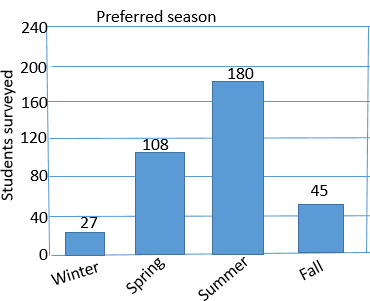
Number of students surveyed who prefer winter =
Number of students surveyed who prefer spring =
Number of students surveyed who prefer summer =
Number of students surveyed who prefer fall =
Total number of students surveyed =
Percent of students surveyed who prefer summer
Percent of students surveyed who prefer summer
Hence,
Percent of students surveyed who prefer summer =
Percent of students surveyed who prefer fall =
Conclusion:
Percent of students surveyed who prefer summer =
Percent of students surveyed who prefer fall =
b.
The number of
b.
Answer to Problem 22E
The number of
Explanation of Solution
Given:
Number of students surveyed who prefer spring =
Calculation:
As per the given problem
Number of students who prefer spring =
Percent of students who are
To find
Hence,
Conclusion:
The number of
c.
The number of students who would prefer a school trip in spring.
c.
Answer to Problem 22E
The total students in the school who would prefer school trip in spring is
Explanation of Solution
Given:
Total number of students in the school =
Number of students surveyed who prefer spring =
Calculation:
As per the given problem
Total number of students in the school =
Number of students surveyed who prefer spring =
Total number of students surveyed =
Percent of students surveyed who prefer spring
=
Since
Assume
Therefore,
The number of students who would prefer school trip in spring =
Hence,
The total students in the school who would prefer school trip in spring
Conclusion:
The total students in the school who would prefer school trip in spring is
Chapter 7 Solutions
EBK PRE-ALGEBRA
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
College Algebra (7th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
Elementary Statistics
- Solutions of inequalitie Google Classroom Mic Is (-3, 2) a solution of 7x+9y > -3? Choose 1 answer: A Yes B No Related content ▶6:06 Testing solutions to inequalities 2 of 4arrow_forwardAre natural logarithms used in real life ? How ? Can u give me two or three ways we can use them. Thanksarrow_forward?arrow_forward
- Solve the equation. Write the smaller answer first. 2 (x-6)² = 36 x = Α x = Previous Page Next Pagearrow_forwardWrite a quadratic equation in factored form that has solutions of x = 2 and x = = -3/5 ○ a) (x-2)(5x + 3) = 0 ○ b) (x + 2)(3x-5) = 0 O c) (x + 2)(5x -3) = 0 ○ d) (x-2)(3x + 5) = 0arrow_forwardA vacant lot is being converted into a community garden. The garden and a walkway around its perimeter have an area of 690 square feet. Find the width of the walkway (x) if the garden measures 14 feet wide by 18 feet long. Write answer to 2 decimal places. (Write the number without units). Hint: add 2x to each of the garden dimensions of 14 x 18 feet to get the total area for the length multiplied by width.arrow_forward
- Solve the rational equation 14 1 + x-6 x x-7 x-7 ○ a) x = 1, x = 8 ○ b) x = 1 ○ c) x = 7 ○ d) x = 1, x = 7arrow_forwardSolve the absolute inequality | x + 5 > 3 ○ a) (-∞, -8] U[-2, ∞0) ☐ b) (-8, -2) c) (-2, ∞0) ○ d) (-∞, - 8) U(-2, ∞0)arrow_forward1) Listen Describe the error in the problem X 3 X x 3 - 2 = 25x = 0 25x 25 x = ±5arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





