
Air enters the evaporator section of a window air conditioner at 100 kPa and 27°C with a volume flow rate of 6 m3/min. The refrigerant-134a at 120 kPa with a quality of 0.3 enters the evaporator at a rate of 2 kg/min and leaves as saturated vapor at the same pressure. Determine the exit temperature of the air and the rate of entropy generation for this process, assuming (a) the outer surfaces of the air conditioner are insulated and (b) heat is transferred to the evaporator of the air conditioner from the surrounding medium at 32°C at a rate of 30 kJ/min.
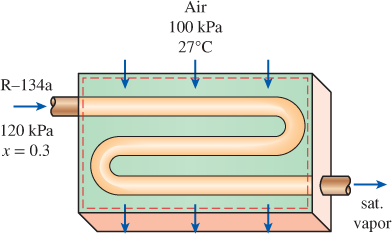
FIGURE P7–180
a)
The exit temperature of air and the entropy generated during the process.
Answer to Problem 180RP
The exit temperature of air is
The entropy generated during the process is
Explanation of Solution
Write the expression to calculate the initial enthalpy of the refrigerant.
Here, initial enthalpy is
Write the expression to calculate the initial entropy of the refrigerant.
Here, initial entropy is
Write the expression to calculate the mass flow rate of air.
Here, mass flow rate of air is
Write the expression for the mass balance of the system.
Here, mass flow rate into the control system is
Write the expression for the energy balance equation for closed system.
Here, rate of energy transfer into the control volume is
Write the expression for the rate of entropy balance for the system.
Here, rate of entropy in the system is
Conclusion:
From Table A-12, “Saturated refrigerant-134a-Pressure table”, Obtain the following properties at saturated pressure of 120 kPa
Saturated liquid enthalpy,
Evaporated enthalpy,
Saturated vapor enthalpy,
Saturated vapor entropy,
Saturated liquid entropy,
Evaporated entropy,
Substitute
Substitute
Refrigerant –134a enters and leaves at the same pressure. Hence,
From Table A-1E, “the molar mass, gas constant and critical–point properties table”, select the gas constant of air at room temperature as
Substitute
Substitute
Here, mass flow rate of refrigerant is
Substitute
Here, mass flow rate of air is
Substitute
From the Table A-2, “Ideal-gas specific heats of various common gases”, select the value of the specific heat at constant pressure value of air as
Substitute 27 C for
Hence, the exit temperature of air is
For the steady flow system, change of entropy in the system is zero.
Substitute
Substitute
Hence, the entropy generated during the process is
b)
The exit temperature of air and the entropy generated during the process.
Answer to Problem 180RP
The exit temperature of air is
The entropy generated during the process is
Explanation of Solution
Write the expression for the energy balance equation for closed system.
Here, rate of energy transfer into the control volume is
Write the expression for the rate of entropy balance for the system.
Here, rate of entropy in the system is
Conclusion:
Substitute
Here, rate of heat gain from the surrounding is
Substitute 27 C for
Hence, the exit temperature of air is
For the steady flow system, change of entropy in the system is zero.
Substitute
Substitute
Hence, the entropy generated during the process is
Want to see more full solutions like this?
Chapter 7 Solutions
THERMODYNAMICS: ENG APPROACH LOOSELEAF
- Qf, Qa,Qm, Qcon,Qfg, Qbd, Qref,Qloss ( meaning, formula, percentage, and importance of higher value na qf, qa etc)arrow_forwardThe beam is supported by a fixed support at point C and a roller at point A. It also has an internal hinge at point B. The beam supports a point load at point D, a moment at point A and a distributed load on segment BC. a. calculate the support reactions at points A and C b. calculate the internal resultant loadings (N, V, M) at points E and F, which lies in the middle between points A and D P = 4 kip Ma = 5 kip-ft w1 = 3 kip/ft and w2 = 4 kip/ft a = 3 ftarrow_forwardFrom the image of the pyramid, I want to find what s1 hat, s2 hat, and s3 hat are. I think s3 hat is just equal to e3 hat right? What about the others?arrow_forward
- Question 1. A tube rotates in the horizontal ry plane with a constant angular velocity w about the z-axis. A particle of mass m is released from a radial distance R when the tube is in the position shown. This problem is based on problem 3.2 in the text. R m 2R Figure 1 x a) Draw a free body diagram of the particle if the tube is frictionless. b) Draw a free body diagram of the particle if the coefficient of friction between the sides of the tube and the particle is = k = p. c) For the case where the tube is frictionless, what is the radial speed at which the particle leaves the tube? d) For the case where there is friction, derive a differential equation that would allow you to solve for the radius of the particle as a function of time. I'm only looking for the differential equation. DO NOT solve it. 1 e) If there is no friction, what is the angle of the tube when the particle exits? • Hint: You may need to solve a differential equation for the last part. The "potentially useful…arrow_forwardQuestion 2. A smooth uniform sphere of mass m and radius r is squeezed between two massless levers, each of length 1, which are inclined at an angle with the vertical. A mechanism at pivot point O ensures that the angles & remain the same at all times so that the sphere moves straight upward. This problem is based on Problem 3-1 in the text. P P r Figure 2 a) Draw appropriate freebody diagrams of the system assuming that there is no friction. b) Draw appropriate freebody diagrams of the system assuming that there is a coefficient of friction between the sphere and the right lever of μ. c) If a force P is applied between the ends of the levers (shown in the diagram), and there is no friction, what is the acceleration of the sphere when = 30°arrow_forwardIf you had a matrix A = [1 2 3; 4 5 6; 7 8 9] and a matrix B = [1 2 3], how would you cross multiply them i.e. what is the cross product of AxB. what would be the cross product of a dyadic with a vector?arrow_forward
- Problem 3: The inertia matrix can be written in dyadic form which is particularly useful when inertia information is required in various vector bases. On the next page is a right rectangular pyramid of total mass m. Note the location of point Q. (a) Determine the inertia dyadic for the pyramid P, relative to point Q, i.e., 7%, for unit vectors ₁₁, 2, 3.arrow_forwardCan you solve for v? Also, what is A x uarrow_forwardThe external loads on the element shown below at the free end are F = 1.75 kN, P = 9.0 kN, and T = 72 Nm. The tube's outer diameter is 50 mm and the inner diameter is 45 mm. Given: A(the cross-sectional area) is 3.73 cm², Moment inertial I is 10.55 cm4, and J polar moment inertial is 21.1 cm4. Determine the following. (1) The critical element(s) of the bar. (2) Show the state of stress on a stress element for each critical element. -120 mm- Farrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





