
The Witch of Agnesi
Many plane curves in mathematics are named after the people who first investigated them, like the folium of Descartes or the spiral of Archimedes. However, perhaps the strangest name for a curve is the witch of Agnesi. Why a witch?
Maria Gaetana Agnesi (1718—1799) was one of the few recognized women mathematicians of eighteenth-century Italy. She wrote a popular book on analytic geometry, published in 1748, which included an interesting curve that had been studied by Fermat in 1630. The mathematician Guido Grandi showed in 1703 how to construct this curve, which he later called the “versiera,” a Latin term for a rope used in sailing. Agnesi used the Italian term for this rope, “versiera,” but in Latin, this same word means a "female goblin.” When Agnesi’s book was translated into English in 1801, the translator used the term “witch” for the curve, instead of rope. The name “witch of Agnesi” has stuck ever since.
The witch of Agnesi is a curve defined as follows: Start with a Circle of radius a so that the points (0, 0) and (0, 2a) are points on the circle (Figure 7.12). Let O denote the origin. Choose any other point A on the circle, and draw the secant line OA. Let B denote the point at which the line OA intersects the horizontal line through (0, 2a). The vertical line through B intersects the horizontal line through A at the point P. As the point A varies, the path that the point P travels is the witch of Agnesi curve for the given circle.
Witch of Agnesi curves have applications in physics, including modeling water waves and distributions of spectral lines. In probability theory, the curve describes the probability density function of the Cauchy distribution. In this project you will parameterize these curves.
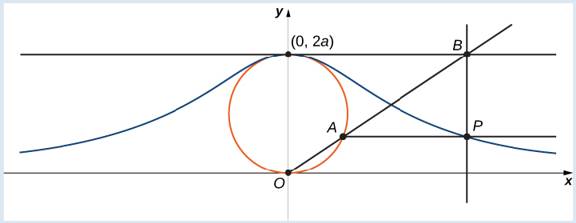
On the figure, label the following points, lengths, and angle:
a. C is the point 011 the x-axis with the same x-Coordinate as A.
b. x is the x-coordinate of P, and y is the y-coordinate of P.
c. E is the point (0, a).
d. F is the point on the line segment 0A such that the line segment EF is perpendicular to the line segment OA.
e. b is the distance from O to F .
f. c is the distance from F to A.
g. d is the distance from O to B.
h. θ is the measure of angle
The goal of this project is to parameterize the witch using θ as a parameter. To do this, write equations for x and y in terms of only θ.
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
Calculus Volume 2
Additional Math Textbook Solutions
Thinking Mathematically (6th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
University Calculus: Early Transcendentals (4th Edition)
Introductory Statistics
Calculus: Early Transcendentals (2nd Edition)
- [) Hwk 29 ✗ WHwk 30 (MA 244-03) (SP X - Logout Cengage Learning X MA244-03 Syllabus_Sprin X b Answered: [) Hwk 29 Hwk X https://www.webassign.net/web/Student/Assignment-Responses/last?dep=36606609 4. [-/3 Points] DETAILS MY NOTES LARLINALG8 7.4.013. Solve the system of first-order linear differential equations. (Use C1 and C2 as constants.) Y1' = -4Y1 Y2' = -12 (y1(t), Y2(t)) = ( 3 Need Help? Read It SUBMIT ANSWER 5. [-/3 Points] DETAILS MY NOTES LARLINALG8 7.4.019. Solve the system of first-order linear differential equations. (Use C1, C2, C3, and C4 as constants.) Y1' = 6y1 Y2' = 2y2 Y3' = -643 Y4' = -2y4 = (y1(t), y2(t), y3(t), Y4(t)) = Need Help? Read It SUBMIT ANSWER G Use the Principal Axes The X G cot(0) - Google Search ☑ B 90% + ASK YOUR TEACHER PRACTICE ANOTHER ill ASK YOUR TEACHER PRACTICE ANOTHER 6. [-/4 Points] DETAILS MY NOTES LARLINALG8 7.4.023. Solve the system of first-order linear differential equations. (Use C1 and C2 as constants.) ASK YOUR TEACHER Y1' = Y1 + 5y2 Y2'…arrow_forwarda. Find the value of A.b. Find pX(x) and py(y).c. Find pX|y(x|y) and py|X(y|x)d. Are x and y independent? Why or why not?arrow_forwardAnalyze the residuals of a linear regression model and select the best response.Criteria is simple evaluation of possible indications of an exponential model vs. linear model) no, the residual plot does not show a curve yes, the residual plot does not show a curve yes, the residual plot shows a curve no, the residual plot shows a curve I selected: yes, the residual plot shows a curve and it is INCORRECT. Can u help me understand why?arrow_forward
- You have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. please do it step by step on excel Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size). Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple…arrow_forward(a) (b) (c) (d) de unique? Answer the following questions related to the linear system x + y + z = 2 x-y+z=0 2x + y 2 3 rewrite the linear system into the matrix-vector form A = 5 Fuse elementary row operation to solve this linear system. Is the solution use elementary row operation to find the inverse of A and then solve the linear system. Verify the solution is the same as (b). give the null space of matrix A and find the dimension of null space. give the column space of matrix A and find the dimension of the column space of A (Hint: use Rank-Nullity Theorem).arrow_forwardplease explain in a clear wayarrow_forward
- [) Hwk 29 SUBMIT ANSWEK Hwk 30 - (MA 244-03) (SP25) || X - Mind Tap Cengage Learning ☑ MA244-03_Syllabus_Spring, 20 × b Answered: [) 90% Hwk 29 Hwk X Rotation of Axes Example - Elimi X + https://www.webassign.net/web/Student/Assignment-Responses/last?dep=36606609 B שי 90% 2. [-/3 Points] DETAILS MY NOTES LARLINALG8 7.4.003. Use the age transition matrix L and age distribution vector X1 to find the age distribution vectors X2 and x3. 0 34 x2 = X3 = L = ↓ ↑ 1 0 0 x1 = 1 0 0 2 20 20 20 Then find a stable age distribution vector. x = t ↓ 1 Need Help? Read It SUBMIT ANSWER 3. [-/3 Points] DETAILS MY NOTES LARLINALG8 7.4.004. Use the age transition matrix L and age distribution vector X1 to find the age distribution vectors x2 and ×3. ill { ASK YOUR TEACHER PRACTICE ANOTHER ASK YOUR TEACHER PRACTICE ANOTHERarrow_forwardHere is data with as the response variable. x y54.4 19.124.9 99.334.5 9.476.6 0.359.4 4.554.4 0.139.2 56.354 15.773.8 9-156.1 319.2Make a scatter plot of this data. Which point is an outlier? Enter as an ordered pair, e.g., (x,y). (x,y)= Find the regression equation for the data set without the outlier. Enter the equation of the form mx+b rounded to three decimal places. y_wo= Find the regression equation for the data set with the outlier. Enter the equation of the form mx+b rounded to three decimal places. y_w=arrow_forwardPoints z1 and z2 are shown on the graph.z1 is at (4 real,6 imaginary), z2 is at (-5 real, 2 imaginary)Part A: Identify the points in standard form and find the distance between them.Part B: Give the complex conjugate of z2 and explain how to find it geometrically.Part C: Find z2 − z1 geometrically and explain your steps.arrow_forward
- [) Hwk 29 SUBMIT ANSWER Hwk 29 - (MA 244-03) (SP25) || X - Mind Tap Cengage Learning ☑ MA244-03_Syllabus_Spring, 20 × b Answered: ( Homework#8 | ba X + https://www.webassign.net/web/Student/Assignment-Responses/submit?dep=36606608&tags=autosave#question3706218_2 2. [-/2.85 Points] DETAILS MY NOTES LARLINALG8 7.3.003. Prove that the symmetric matrix is diagonalizable. (Assume that a is real.) 0 0 a A = a 0 a 0 0 Find the eigenvalues of A. (Enter your answers as a comma-separated list. Do not list the same eigenvalue multiple times.) λ= Find an invertible matrix P such that P-1AP is diagonal. P = Which of the following statements is true? (Select all that apply.) ☐ A is diagonalizable because it is a square matrix. A is diagonalizable because it has a determinant of 0. A is diagonalizable because it is an anti-diagonal matrix. A is diagonalizable because it has 3 distinct eigenvalues. A is diagonalizable because it has a nonzero determinant. A is diagonalizable because it is a symmetric…arrow_forwardA polar curve is represented by the equation r1 = 7 + 4cos θ.Part A: What type of limaçon is this curve? Justify your answer using the constants in the equation.Part B: Is the curve symmetrical to the polar axis or the line θ = pi/2 Justify your answer algebraically.Part C: What are the two main differences between the graphs of r1 = 7 + 4cos θ and r2 = 4 + 4cos θ?arrow_forwardA curve, described by x2 + y2 + 8x = 0, has a point A at (−4, 4) on the curve.Part A: What are the polar coordinates of A? Give an exact answer.Part B: What is the polar form of the equation? What type of polar curve is this?Part C: What is the directed distance when Ø = 5pi/6 Give an exact answer.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,  Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning



