Chapter 7, Problem 99P

(a)

To determine

The magnitude of the combined force of friction at $20\text{m}/\text{s}$ and at $30\text{m}/\text{s}$ .

Answer to Problem 99P

The magnitude of the combined force of friction at $20\text{m}/\text{s}$ is $491\text{N}$ and at $30\text{m}/\text{s}$ is $981\text{N}$ .

Explanation of Solution

Given:

On a $2.87°$ hill, speed of car is $20\text{m}/\text{s}$ ,on a $5.74°$ hill, speed of car is $30\text{m}/\text{s}$ and total mass of the car is $1000\text{kg}$ .

Formula used:

Magnitude of force of friction at $20\text{m}/\text{s}$ is $F_{20}$ and magnitude of force of friction at $30\text{m}/\text{s}$ is $F_{30}$ .

The diagram representing the situation is given below.

  

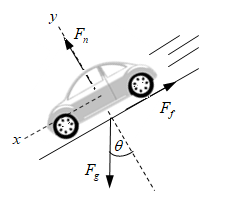
Write the equation of resultant along the incline in equilibrium position.

  $\sum F_x=0$

Here, $F_x$ is summation of all the forces along incline.

Substitute $mg\sin \theta -F_f$ for $F_x$ in above equation.

  $mg\sin \theta -F_f=0$

Rearrange above equation.

  $F_f=mg\sin \theta$ …... (1)

Here, $mg\sin \theta$ is component of $F_g$ along the incline and $F_f$ is the frictional force.

Calculation:

Whenspeed of car is $20\text{m}/\text{s}$ .

Substitute $2.87°$ for $\theta$ , $1000\text{kg}$ for $m$ and $9.81{\text{m/s}}^{\text{2}}$ for $g$ in equation (1).

  $\begin{array}{c}{F}_{20}=\left(1000\text{kg}\right)\left(9.81{\text{m/s}}^{\text{2}}\right)\sin \left(2.87°\right)\\ \approx 491\text{N}\end{array}$

Whenspeed of car is $30\text{m}/\text{s}$ .

Substitute $5.74°$ for $\theta$ , $1000\text{kg}$ for $m$ and $9.81{\text{m/s}}^{\text{2}}$ for $g$ in equation (1).

  $\begin{array}{c}{F}_{30}=\left(1000\text{kg}\right)\left(9.81{\text{m/s}}^{\text{2}}\right)\sin \left(5.74°\right)\\ \approx 981\text{N}\end{array}$

Conclusion:

Thus, the magnitude of the combined force of friction at $20\text{m}/\text{s}$ is $491\text{N}$ and at $30\text{m}/\text{s}$ is $981\text{N}$ .

(b)

To determine

The power delivered by the engine to drive the car on a level road at $20\text{m}/\text{s}$ and at $30\text{m}/\text{s}$ .

Answer to Problem 99P

The power delivered by the engine to drive the car on a level road at $20\text{m}/\text{s}$ and at $30\text{m}/\text{s}$ is $\text{9}\text{.8}\text{kW}$ and $\text{29}\text{kW}$ respectively.

Explanation of Solution

Given:

On a $2.87°$ hill, speed of car is $20\text{m}/\text{s}$ , on a $5.74°$ hill, speed of car is $30\text{m}/\text{s}$ , total mass of the car is $1000\text{kg}$ the magnitude of the combined force of friction at $20\text{m}/\text{s}$ is $491\text{N}$ and at $30\text{m}/\text{s}$ is $981\text{N}$ .

Formula used:

Power delivered by the engine to drive the car on a level road at $20\text{m}/\text{s}$ is $P_{20}$ and power delivered by the engine to drive the car on a level road at $30\text{m}/\text{s}$ is $P_{30}$ .

Power delivered by the engine to drive the car on a level road in order to overcome friction is calculated by the expression given below.

Write the expression for power delivered.

  $P=F_{f}v$ ........(2)

Here, $P$ is the power delivered and $v$ is the speed of the car.

Calculation:

Substitute $491\text{N}$ for $F_f$ and $20\text{m}/\text{s}$ for $v$ in equation (2).

  $\begin{array}{c}{P}_{20}=\left(491\text{N}\right)\left(20\text{m}/\text{s}\right)\\ =9820\text{W}\\ \text{=9}\text{.8}\text{kW}\end{array}$

Substitute $981\text{N}$ for $F_f$ and $30\text{m}/\text{s}$ for $v$ in equation (2).

  $\begin{array}{c}{P}_{30}=\left(981\text{N}\right)\left(30\text{m}/\text{s}\right)\\ =29430\text{W}\\ \text{=29}\text{kW}\end{array}$

Conclusion:

Thus, the power delivered by the engine to drive the car on a level road at $20\text{m}/\text{s}$ and at $30\text{m}/\text{s}$ is $\text{9}\text{.8}\text{kW}$ and $\text{29}\text{kW}$ respectively.

(c)

To determine

The angle of the steepest incline up which can be maintained by car at steady speed of $20\text{m}/\text{s}$ .

Answer to Problem 99P

The angle of the steepest incline up which can be maintained by car at steady speed of $20\text{m}/\text{s}$ is $8.8°$ .

Explanation of Solution

Given:

On a $2.87°$ hill, speed of car is $20\text{m}/\text{s}$ , on a $5.74°$ hill, speed of car is $30\text{m}/\text{s}$ , total mass of the car is $1000\text{kg}$ the magnitude of the combined force of friction at $20\text{m}/\text{s}$ is $491\text{N}$ and at $30\text{m}/\text{s}$ is $981\text{N}$ .

Formula used:

The diagram representing the situation is given below.

  

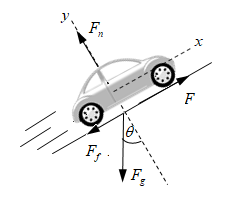
Write the equation of resultant along the incline in equilibrium position.

  $\sum F_x=0$

Here, $F_x$ is summation of all the forces along incline.

Substitute $F-mg\sin \theta -F_f$ for $F_x$ in above equation.

  $F-mg\sin \theta -F_f=0$

Rearrange above equation.

  $F=mg\sin \theta +F_f$

Here, $F$ is the external force.

Substitute $\frac{P}{v}$ for $F$ in above equation.

  $\frac{P}{v}=mg\sin \theta +F_f$

Rearrange above equation for $\theta$ .

  $\theta ={\sin }^{-1}\left[\frac{\frac{P}{v}-F_f}{mg}\right]$ …... (3)

Calculation:

Substitute $20\text{m}/\text{s}$ for $v$ , $40\text{kW}$ for $P$ , $1000\text{kg}$ for $m$ , $491\text{N}$ for $F_f$ and $9.81{\text{m/s}}^{\text{2}}$ for $g$ in equation (3).

  $\begin{array}{c}\theta ={\sin }^{-1}\left[\frac{\frac{40\text{kW}}{20\text{m}/\text{s}}-491\text{N}}{\left(1000\text{kg}\right)\left(9.81{\text{m/s}}^{\text{2}}\right)}\right]\\ ={\sin }^{-1}\left[\frac{1509}{9810}\right]\\ =8.8°\end{array}$

Conclusion:

Thus, the angle of the steepest incline up which can be maintained by car at steady speed of $20\text{m}/\text{s}$ is $8.8°$ .

(d)

To determine

The total useful work in kilometers per liter when engine goes at $30\text{m}/\text{s}$ .

Answer to Problem 99P

The total useful work in kilometers per liter when engine goes at $30\text{m}/\text{s}$ is $6.36\text{km/L}$ .

Explanation of Solution

Given:

The magnitude of the combined force of friction at $20\text{m}/\text{s}$ is $491\text{N}$ and at $30\text{m}/\text{s}$ is $981\text{N}$ .

Formula used:

Write the expression for work done by engine.

  $W=F\Delta s$

Here, $W$ is the work done, $F$ is the force and $\Delta s$ is the distance in kilometers per liter.

From the condition of equivalence:

  $F_{20}\Delta s_{20}=F_{30}\Delta s_{30}$

Here, $\Delta s_{20}$ is the distance in kilometers per liter when speed is $20\text{m/s}$ and $\Delta s_{30}$ is the distance in kilometers per liter when speed is $30\text{m/s}$ .

Rearrange above equation.

  $\Delta s_{30}=\frac{F_{20}}{F_{30}}\Delta s_{20}$ ........(4)

Calculation:

Substitute $491\text{N}$ for $F_{20}$ , $981\text{N}$ for $F_{30}$ and $12.7\text{km/L}$ for $s_{20}$ in equation (4).

  $\begin{array}{c}\Delta s_{30}=\frac{491\text{N}}{981\text{N}}\left(12.7\text{km/L}\right)\\ =6.36\text{km/L}\end{array}$

Conclusion:

Thus, the total useful work in kilometers per liter when engine goes at $30\text{m}/\text{s}$ is $6.36\text{km/L}$ .