Chapter 7, Problem 97P

(a)

To determine

The height of point B above the ground, if the car at A barely makes it up the hill at B.

Answer to Problem 97P

The point B is at a height of $17\text{ m}$ above the ground.

Explanation of Solution

Given:

The mass of the roller- coaster carriage

  $m=500\text{ kg}$

Speed at point A

  $v_A=12\text{ m/s}$

Height of A above the ground

  $h=10\text{ m}$

Formula used:

The carriage at A has both potential and kinetic energies.

  $E_A=mgh+\frac{1}{2}m{v}_A^2$

However, the carriage just manages to make it over the point B . This means that at B the carriage has no kinetic energy, it has potential energy alone by virtue of its position.

Therefore, the energy at B is given by,

  $E_B=mg{h}_B$

Apply the law of conservation of energy to the motion of the carriage between points A and B .

  $E_A=E_B$

Therefore,

  $mgh+\frac{1}{2}m{v}_A^2=mg{h}_B$

Hence,

  $h_B=h+\frac{v_A^2}{2g}$............(1)

Calculation:

Substitute the values of the variables in equation (1).

  $\begin{array}{c}{h}_B=h+\frac{v_A^2}{2g}\\ =\left(10\text{ m}\right)+\frac{{\left(12\text{ m/s}\right)}^2}{2\left(9.81{\text{ m/s}}^2\right)}\\ =17.3\text{ m}\\ \text{=17 m}\end{array}$

Conclusion:

Thus, the point B is at a height of $17\text{ m}$ above the ground.

(b)

To determine

The magnitude of the force exerted by the track on the car if it is just able to make it over the hill at B .

Answer to Problem 97P

  $4.91\text{ kN}$

Explanation of Solution

Given:

The mass of the roller- coaster carriage

  $m=500\text{ kg}$

Radius of curvature of the hill located at B .

  $r_B=20\text{ m}$

Formula used:

The car crosses over a hill of radius of curvature $r_B$ and for this it requires to be provided with a centripetal force. Since it just manages to cross over the point B , the normal force acting on the car is zero. The weight of the car $mg$

provides the centripetal force. This is shown in Figure 1, below:

  

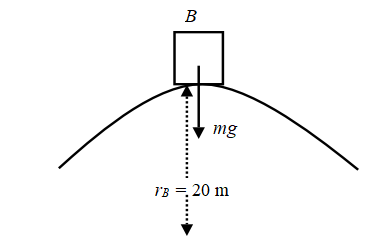
     Figure 1

Thus, the force exerted by the track on the car is the centripetal force and this is equal to the weight of the car.

  $F=mg$............(2)

Calculation:

Substitute the given values of the variables in equation (2).

  $\begin{array}{c}F=mg\\ =\left(500\text{ kg}\right)\left(9.81{\text{ m/s}}^2\right)\\ =4.91\times {10}^3\text{N}\\ =4.91\text{ kN}\end{array}$

Conclusion:

Thus, the magnitude of the force exerted by the track on the car at point B is found to be $4.91\text{ kN}$

(c)

To determine

The acceleration of the car at point C .

Answer to Problem 97P

  $4.91{\text{ m/s}}^2$

Explanation of Solution

Given:

The angle of the incline

  $\theta =30°$

Formula used:

The point C is on an incline and when no dissipative forces act on the car, the car moves down with a constant acceleration. Modelling the motion of the car at point C as that over an incline, the free body diagram of the car is drawn.

  

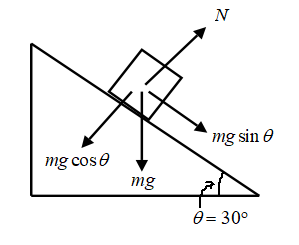
     Figure 2

The car is under the action of two forces: (i) the weight $mg$ of the car acting vertically downwards and (ii) the normal contact force N acting vertically upwards. The weight $mg$ is resolved into two components- $mg\sin \theta$ down the plane and $mg\cos \theta$ perpendicular to the incline, as shown in Figure 2.

Since the block is in equilibrium along the direction perpendicular to the incline,

  $N=mg\cos \theta$

However, the component $mg\sin \theta$ is unbalanced and the car accelerates down the incline. Applying Newton’s second law,

  $ma=mg\sin \theta$

Hence,

  $a=g\sin \theta$............(3)

Calculation:

Substitute the values of the variables in equation (3) and calculate the value of the acceleration at point C .

  $\begin{array}{c}a=g\sin \theta \\ =\left(9.81{\text{ m/s}}^2\right)\left(\sin 30°\right)\\ =4.91{\text{ m/s}}^2\end{array}$

Conclusion:

Thus, the acceleration of the car at point C is found to be $4.91{\text{ m/s}}^2$ .

(d)

To determine

The force exerted by the track on the car at point D .

Answer to Problem 97P

The force exerted by the track on the car at point D is found to be $\text{13 kN}$ and it is directed upwards.

Explanation of Solution

Given:

The mass of the roller- coaster carriage

  $m=500\text{ kg}$

Radius of curvature of the valley located at D .

  $r_D=20\text{ m}$

Height of point B above the ground

  $h_B=17.3\text{ m}$

Formula used:

The point D is located at the ground level. Assuming the car has zero velocity at B , its energy is entirely potential at B . This energy is converted into kinetic energy at D .

Using the law of conservation of energy

  $mg{h}_B=\frac{1}{2}m{v}_D^2$............(4)

At D the car traces an arc of radius $r_D=20\text{ m}$ . The forces acting on the car are depicted in the Figure 3 .

  

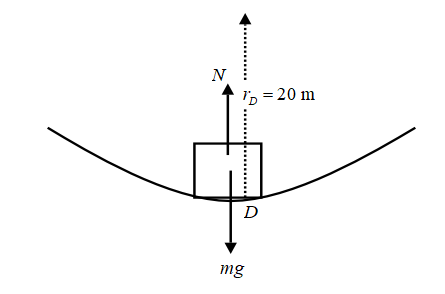
     Figure 3

The car is acted upon by two forces- (i) Its weight $mg$ acting downwards and (ii) the normal force N acting upward. The force exerted by the track on the car is the normal contact force.

The total inward force provides the centripetal force, which is given by the expression $\frac{m{v}_D^2}{r_D}$ .

Therefore,

  $N-mg=\frac{m{v}_D^2}{r_D}$

Hence,

  $N=\frac{m{v}_D^2}{r_D}+mg$............(5)

From equation (4),

  $m{v}_D^2=2mg{h}_B$

Equation (5), therefore can be simplified as follows:

  $\begin{array}{c}N=\frac{m{v}_D^2}{r_D}+mg\\ =\frac{2mg{h}_B}{r_D}+mg\end{array}$

Therefore,

  $N=mg\left(\frac{2h_B}{r_D}+1\right)$............(6)

Calculation:

Substitute the values of the variables in equation (6).

  $\begin{array}{c}N=mg\left(\frac{2h_B}{r_D}+1\right)\\ =\left(500\text{ kg}\right)\left(9.81{\text{ m/s}}^2\right)\left[\frac{2\left(17.3\text{ m}\right)}{\left(20\text{ m}\right)}+1\right]\\ =1.34\times {10}^4\text{N}\\ =13\text{ kN}\end{array}$

Conclusion:

Thus, the force exerted by the track on the car at point D is found to be $\text{13 kN}$ and it is directed upwards.

(e)

To determine

The magnitude and the direction of the force exerted by the track at the point F which lies in the middle of a banked horizontal curve of radius 30 m.

Answer to Problem 97P

The magnitude of the force exerted by the track on the car is $5.5\text{ kN}$ and it is directed at an angle $\text{64}°$to the horizontal.

Explanation of Solution

Given:

The mass of the roller- coaster carriage

  $m=500\text{ kg}$

Height of point F above the ground

  $h_F=10\text{ m}$

Radius of curvature of the path at F

  $r_F=30\text{ m}$

Speed at point A

  $v_A=12\text{ m/s}$

Formula used:

The car is at the same height as point A . The system is under the action of gravitational forces alone. Hence the speed at F is equal to the speed at A .

  $v_F=v_A$

The car is on a horizontal banked road. The forces acting on the car are shown in Figure 4.

  

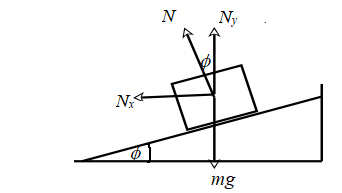
     Figure 4

The forces acting on the car are (i) weight $mg$ acting downwards and (ii) the normal force N acting upward. The force exerted by the track on the car is the normal contact force.

The normal force N is resolved into two components- $N_x$ along the radius of the path and $N_y$ perpendicular to it.

The car is in equilibrium along the y direction.

Therefore,

  $N_y=mg$............(7)

The component $N_x$ provides the centripetal force.

  $N_x=\frac{m{v}_F^2}{r_F}$............(8)

The force exerted by the track on the car is given by,

  $N=\sqrt{N_x^2+N_y^2}$............(9)

The angle made by the force N with the horizontal is given by,

  $\alpha ={\tan }^{-1}\left(\frac{N_y}{N_x}\right)$.............(10)

Calculation:

Substitute the values of the variables in equation (7) and calculate the value of $N_y$ .

  $\begin{array}{c}{N}_y=mg\\ =\left(500\text{ kg}\right)\left(9.81{\text{ m/s}}^2\right)\\ =4.91\times {10}^3\text{N}\\ =4.91\text{ kN}\end{array}$

Substitute the values of the variables in equation (8) and calculate the value of $N_x$ .

  $\begin{array}{c}{N}_x=\frac{m{v}_F^2}{r_F}\\ =\frac{\left(500\text{ kg}\right){\left(12\text{ m/s}\right)}^2}{\left(30\text{ m}\right)}\\ =2.40\times {10}^3\text{N}\\ =2.40\text{ kN}\end{array}$

Substitute the values of the variables in equation (9) and calculate the magnitude of the force exerted by the track on the car.

  $\begin{array}{c}N=\sqrt{N_x^2+N_y^2}\\ =\sqrt{{\left(2.40\text{ kN}\right)}^2+{\left(4.91\text{ kN}\right)}^2}\\ =5.465\text{ kN}\\ =5.5\text{ kN}\end{array}$

Calculate the angle made by the force with the horizontal using equation (10).

  $\begin{array}{c}\alpha ={\tan }^{-1}\left(\frac{N_y}{N_x}\right)\\ ={\tan }^{-1}\left[\frac{\left(4.91\text{ kN}\right)}{\left(2.40\text{ kN}\right)}\right]\\ =64.1°\\ =64°\end{array}$

Conclusion:

Thus, the magnitude of the force exerted by the track on the car is $5.5\text{ kN}$ and it is directed at an angle $\text{64}°$to the horizontal.

(f)

To determine

The magnitude of the braking force that needs to be applied at G so that the car comes to rest in a distance of 25 m.

Answer to Problem 97P

The magnitude of the braking force that needs to be applied at G so that the car comes to rest in a distance of 25 m is $1.4\text{ kN}$ .

Explanation of Solution

Given:

The mass of the roller-coaster carriage

  $m=500\text{ kg}$

Speed at point A

  $v_A=12\text{ m/s}$

Distance travelled before stopping

  $\Delta x=25\text{ m}$

The final velocity of the car

  $v_f=0$

Formula used:

The point G is at the same height as points F and A . Therefore, the speed at G is equal to the speed at A .

  $v_G=v_A$

The acceleration of the car is determined using the expression,

  $v_f^2=v_G^2+2a\Delta x$............(11)

The braking force can be determined using Newton’s second law:

  $F=ma$............(12)

Calculation:

Substitute the values of the variables in equation (11) and calculate the acceleration at G .

  $\begin{array}{c}a=-\frac{{\left(12\text{ m/s}\right)}^2}{2\left(25\text{ m}\right)}\\ =-2.88{\text{ m/s}}^2\end{array}$

The negative sign shows that the acceleration is directed opposite to the car’s velocity.

Calculate the braking force using equation (12).

  $\begin{array}{c}F=ma\\ =\left(500\text{ kg}\right)\left(2.88{\text{ m/s}}^2\right)\\ =1.44\times {10}^3\text{N}\\ =1.4\text{ kN}\end{array}$

Conclusion:

Thus, the magnitude of the braking force that needs to be applied at G so that the car comes to rest in a distance of 25 m is $1.4\text{ kN}$ .