
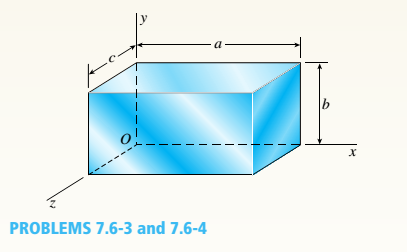
-3 An element of aluminum in the form of a rectangular parallelepiped (see figure) of dimensions a = 5.5 in., h = 4.5 in, and c = 3.5 in. is subjected to iriaxial stresses = 12,500 psi, o. = —5000 psi, and ci. = —1400 psi acting on the x,i, and z faces, respectively.
Determine the following quantities: (a) the maxim um shear stress in the material; (b) the changes ..la, .11. and 1c in the dimensions of the element:
(C) the change .IJ’ in the volume: (d) the strain energy U stored in the element: (e) the maximum value of cr1
when the change in volume must be limited to 0.021%; and (f) the required value of o when the strain energy must be 900 in.-lb. (Assume E = 10,400 ksi and v = 0.33.)
(a)
The maximum shear stress in the material.
Answer to Problem 7.6.3P
The maximum shear stress on the material is
Explanation of Solution
Given information:
The aluminium element of length
Explanation:
Write the expression for the maximum shear stress.
Here, the maximum shear stress is
Calculation:
Since no shear stresses act on the parallelepiped,
Substitute,
Conclusion:
The maximum shear stress on the material is
(b)
The changes in the dimensions of the element.
Answer to Problem 7.6.3P
The change in length is
The change in height is
The change in width is
Explanation of Solution
Write the expression for the strain along
Here, the strain in the
Write the expression for strain in
Here, the strain in
Write the expression for strain in
Here, the strain in
Write the expression for the change in length.
Here, the length of element is
Write the expression for change in height.
Here, the height of element is
Write the expression for the change in width.
Here, the width of the element is
Calculation:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Conclusion:
The change in length is
The change in height is
The change in width is
(c)
The change in the volume of the element.
Answer to Problem 7.6.3P
The change in the volume is
Explanation of Solution
Write the expression for the change in the volume.
Here, the change in volume is
Calculation:
Substitute
Conclusion:
The change in the volume is
(d)
The strain energy stored in the element.
Answer to Problem 7.6.3P
The strain energy stored in the element is
Explanation of Solution
Write the expression for the strain energy.
Here, the strain energy is
Calculation:
Substitute
Conclusion:
The strain energy stored in the element is
(e)
The maximum value of normal stress along the
Answer to Problem 7.6.3P
The maximum value of normal stress along the
Explanation of Solution
Given information:
The change in volume is limited to
Explanation:
Write the expression for the change in volume.
Calculation:
Substitute
Conclusion:
The maximum value of normal stress along the
(f)
The required value of normal stress along the
Answer to Problem 7.6.3P
The required value of the normal stress along the
Explanation of Solution
Given information:
The strain energy of the system is
Explanation:
Write the expression for the strain energy in terms of stresses using Hooke’s law.
Calculation:
Substitute
Solve the quadratic equation for obtaining the value of
Conclusion:
The required value of the normal stress along the
Want to see more full solutions like this?
Chapter 7 Solutions
Bundle: Mechanics Of Materials, Loose-leaf Version, 9th + Mindtap Engineering, 1 Term (6 Months) Printed Access Card
- Generate the kinematic diagram of the following mechanisms using the given symbols. Then, draw their graphs and calculate their degrees of freedom (DoF) using Gruebler's formula. PUNTO 2. PUNTO 3. !!!arrow_forwardCreate a schematic representation of the following mechanisms using the given symbols and draw their graphs. Then, calculate their degrees of freedom (DoF) using Gruebler's formula. PUNTO 6. PUNTO 7.arrow_forwardhow the kinematic diagram of the following mechanisms would be represented using the given symbols? PUNTO 0. PUNTO 1. °arrow_forward
- Create a schematic representation of the following mechanisms using the given symbols and draw their graphs. Then, calculate their degrees of freedom (DOF) using Gruebler's formula. PUNTO 4. PUNTO 5. (0) Groundarrow_forwardDraw the graph of ALL the mechanisms and calculate their DoF using Gruebler's formula. PUNTO 0. PUNTO 1.arrow_forwardAn adjustable support. Construction designed to carry vertical load and is adjusted by moving the blue attachment vertically. The link is articulated at both ends (free to rotate) and can therefore only transmit power axially. Analytically calculate the force to which the link is subjected? Calculate analytically rated voltage in the middle of the link.? F=20kN Alpha 30 deg Rel 225 Mpans:5arrow_forward
- A swivel crane where the load is moved axially along the beam through the wagon to which the hook is attached. Round bar with a diameter of ∅30 mm. The support beam is articulated at both ends (free to rotate) and can therefore only transmit force axially. Calculate reaction force in the x-direction at point A? Calculate analytical reaction force in the y-direction of point A? Calculate nominal stress in the middle of the support beam?Lengt 5 mAlfa 25 degX=1.5mIPE300-steelmass:1000 kgarrow_forwardgot wrong answers help pleasearrow_forwardA crate weighs 530 lb and is hung by three ropes attached to a steel ring at A such that the top surface is parallel to the xy plane. Point A is located at a height of h = 42 in above the top of the crate directly over the geometric center of the top surface. Use the dimensions given in the table below to determine the tension in each of the three ropes. 2013 Michael Swanbom cc00 BY NC SA ↑ Z C b B У a D Values for dimensions on the figure are given in the following table. Note the figure may not be to scale. Variable Value a 30 in b 43 in 4.5 in The tension in rope AB is 383 x lb The tension in rope AC is 156 x lb The tension in rope AD is 156 x lbarrow_forward
- A block of mass m hangs from the end of bar AB that is 7.2 meters long and connected to the wall in the xz plane. The bar is supported at A by a ball joint such that it carries only a compressive force along its axis. The bar is supported at end B by cables BD and BC that connect to the xz plane at points C and D respectively with coordinates given in the figure. Cable BD is elastic and can be modeled as a linear spring with a spring constant k = 400 N/m and unstretched length of 6.34 meters. Determine the mass m, the compressive force in beam AB and the tension force in cable BC. Z C D (c, 0, d) (a, 0, b) A B y f m cc 10 BY NC SA 2016 Eric Davishahl x Values for dimensions on the figure are given in the following table. Note the figure may not be to scale. Variable Value a 8.1 m b 3.3 m с 2.7 m d 3.9 m e 2 m f 5.4 m The mass of the block is 68.8 The compressive force in bar AB is 364 × kg. × N. The tension in cable BC is 393 × N.arrow_forwardThe airplane weighs 144100 lbs and flies at constant speed and trajectory given by 0 on the figure. The plane experiences a drag force of 73620 lbs. 0 a.) If 11.3°, determine the thrust and lift forces = required to maintain this speed and trajectory. b.) Next consider the case where is unknown, but it is known that the lift force is equal to 7.8 times the quantity (Fthrust Fdrag). Compute the resulting trajectory angle and the lift force in this case. Use the same values for the weight and drag forces as you used for part a. 20. YAAY' Farag Ө Fthrust CC + BY NC SA 2013 Michael Swanbom Flift Fweight The lift force acts in the y' direction. The weight acts in the negative y direction. The thrust and drag forces act in the positive and negative x' directions respectively. Part (a) The thrust force is equal to 101,855 ☑ lbs. The lift force is equal to 141,282 ☑ lbs. Part (b) The trajectory angle 0 is equal to 7.31 ✓ deg. The lift force is equal to 143,005 ☑ lbs.arrow_forwardsimply supported beam has a concentrated moment M, applied at the left support and a concentrated force F applied at the free end of the overhang on the right. Using superposition, determine the deflection equations in regions AB and BC.arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
