Chapter 7, Problem 7.38P

A square filamentary differential current loop, dL on a side, is centered at the origin in the z = 0 plane in free space. The current I flows generally in the a_D direction, (a) Assuming that r dL, and following a method similar to that in Section 4.7, show that $dA=\frac{\mu \varphi I{\left(dL\right)}^2\sin \theta }{4x{r}^2}a\varphi$

(b) Show that $dH=\frac{I{\left(dL\right)}^2}{4x{r}^2}\left(2\cos \theta a_r+\sin \theta a\theta \right)$

The square loop is one form of a magnetic dipole.

To determine

(a)

To prove:

$dA=\frac{{\mu }_{o}I{(dL)}^2\sin \theta }{4\pi r^2}{a}_{\varphi }$

Explanation of Solution

Given info:

The centre of the square differential current loop origin in the plane z = 0. The current I is flowing in the $a_{\varphi }$ direction.

Calculation:

We assume that $r>>dL$ and consider the differential vector potential equation,

   $dA=\frac{{\mu }_{o}IdL}{4\pi R}$

Consider the figures below y-displaced elements. Considering the observation point is far than the lines $r,R_1,R_2$ which are mostly parallel.

  

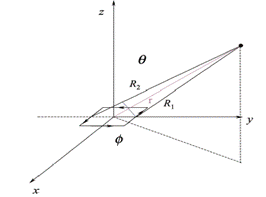
  Figure 1

  

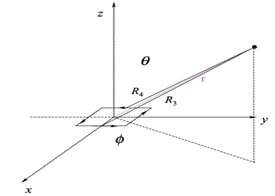
  Figure 2

The net potential can be written as,

   $dA=\frac{{\mu }_{o}IdL}{4\pi }\left[a_x\left(\frac{1}{R_2}-\frac{1}{R_1}\right)+a_y\left(\frac{1}{R_3}-\frac{1}{R_4}\right)\right]$

From figure (1) and figure (2) we can take,

   $\begin{array}{l}{R}_1=r-\left[\frac{dL}{2}{a}_y\cdot a_r\right]\\ R_2=r+\left[\frac{dL}{2}{a}_y\cdot a_r\right]\\ R_3=r-\left[\frac{dL}{2}{a}_x\cdot a_r\right]\\ R_4=r+\left[\frac{dL}{2}{a}_x\cdot a_r\right]\end{array}$

We know that $a_x.a_r=\sin \theta \cos \varphi$ , $a_y.a_r=\sin \theta \sin \varphi$

By substituting the values in the above equation, we get,

   $\begin{array}{l}{R}_1=r-\left[\frac{dL}{2}\sin \theta \sin \varphi \right]\\ R_2=r+\left[\frac{dL}{2}\sin \theta \sin \varphi \right]\\ R_3=r-\left[\frac{dL}{2}\sin \theta \cos \varphi \right]\\ R_4=r+\left[\frac{dL}{2}\sin \theta \cos \varphi \right]\end{array}$

We can write $dA$ as,

   $dA=\frac{{\mu }_{o}IdL}{4\pi }\left[a_x\left(\frac{1}{R_2}-\frac{1}{R_1}\right)+a_y\left(\frac{1}{R_3}-\frac{1}{R_4}\right)\right]$

   $\begin{array}{l}dA=\frac{{\mu }_{o}IdL}{4\pi }\left[\begin{array}{l}{a}_x\left(\frac{1}{r+\left[\frac{dL}{2}\sin \theta \sin \varphi \right]}-\frac{1}{r-\left[\frac{dL}{2}\sin \theta \sin \varphi \right]}\right)\\ +a_y\left(\frac{1}{r-\left[\frac{dL}{2}\sin \theta \cos \varphi \right]}-\frac{1}{r+\left[\frac{dL}{2}\sin \theta \cos \varphi \right]}\right)\end{array}\right]\\ dA=\frac{{\mu }_{o}IdL}{4\pi r}\left[\begin{array}{l}{a}_x\left(\frac{1}{1+\left[\frac{dL}{2r}\sin \theta \sin \varphi \right]}-\frac{1}{1-\left[\frac{dL}{2r}\sin \theta \sin \varphi \right]}\right)\\ +a_y\left(\frac{1}{1-\left[\frac{dL}{2r}\sin \theta \cos \varphi \right]}-\frac{1}{1+\left[\frac{dL}{2r}\sin \theta \cos \varphi \right]}\right)\end{array}\right]\\ dA=\frac{{\mu }_{o}IdL}{4\pi r}\left[\begin{array}{l}{a}_x\left({\left(1+\left[\frac{dL}{2r}\sin \theta \sin \varphi \right]\right)}^{-1}-{\left(1-\left[\frac{dL}{2r}\sin \theta \sin \varphi \right]\right)}^{-1}\right)\\ +a_y\left({\left(1-\left[\frac{dL}{2r}\sin \theta \cos \varphi \right]\right)}^{-1}-{\left(1+\left[\frac{dL}{2r}\sin \theta \cos \varphi \right]\right)}^{-1}\right)\end{array}\right]\end{array}$

We have considered $r>>dL$

   $\Rightarrow \frac{dL}{r}<<1$ we can write the above equation as:

   $dA=\frac{{\mu }_{o}IdL}{4\pi r}\left[\begin{array}{l}{a}_x\left(\left(1-\left[\frac{dL}{2r}\sin \theta \sin \varphi \right]\right)-\left(1+\left[\frac{dL}{2r}\sin \theta \sin \varphi \right]\right)\right)\\ +a_y\left(\left(1+\left[\frac{dL}{2r}\sin \theta \cos \varphi \right]\right)-\left(1-\left[\frac{dL}{2r}\sin \theta \cos \varphi \right]\right)\right)\end{array}\right]$

   $dA=\frac{{\mu }_{o}IdL}{4\pi r}\left[a_x\left(-\frac{dL}{r}\sin \theta \sin \varphi \right)+a_y\left(\frac{dL}{r}\sin \theta \cos \varphi \right)\right]$

   $dA=\frac{{\mu }_{o}I\sin \theta {\left(dL\right)}^2}{4\pi r^2}\left[a_x\left(-\sin \varphi \right)+a_y\left(\cos \varphi \right)\right]$

   $dA=\frac{{\mu }_{o}I\sin \theta {\left(dL\right)}^2}{4\pi r^2}{a}_{\varphi }$

Thus, the relation is proved.

To determine

(b)

To prove:

$dH=\frac{I{\left(dL\right)}^2}{4\pi r^3}\left(2\cos \theta a_r+\sin \theta a_{\theta }\right)$

Explanation of Solution

Given info:

The centre of the square differential current loop origin in the plane z = 0. The current I is flowing in the $a_{\varphi }$ direction.

Calculation:

We know that $dH=\left(\frac{1}{{\mu }_o}\right)\nabla \times dA$ , We got $dA=\frac{{\mu }_{o}I\sin \theta {\left(dL\right)}^2}{4\pi r^2}{a}_{\varphi }$

   $\nabla \times dA=\frac{1}{r\sin \theta }\frac{\partial (dA\sin \theta )}{\partial \theta }{a}_r-\frac{1}{r}\frac{\partial \left(rdA\right)}{\partial r}{a}_{\theta }$

Substitute $dA=\frac{{\mu }_{o}I\sin \theta {\left(dL\right)}^2}{4\pi r^2}$

   $\nabla \times dA=\frac{1}{r\sin \theta }\frac{\partial \left(\frac{{\mu }_{o}I{\sin }^2\theta {\left(dL\right)}^2}{4\pi r^2}\right)}{\partial \theta }{a}_r-\frac{1}{r}\frac{\partial \left(\frac{{\mu }_{o}I\sin \theta {\left(dL\right)}^2}{4\pi r}\right)}{\partial r}{a}_{\theta }$

   $\nabla \times dA=\frac{1}{r\sin \theta }\left(\frac{2{\mu }_{o}I\sin \theta \cos \theta {\left(dL\right)}^2}{4\pi r^2}\right)a_r+\frac{1}{r^3}\left(\frac{{\mu }_{o}I\sin \theta {\left(dL\right)}^2}{4\pi }\right)a_{\theta }$

   $\nabla \times dA=\left(\frac{{\mu }_{o}I\cos \theta {\left(dL\right)}^2}{2\pi r^3}\right)a_r+\left(\frac{{\mu }_{o}I\sin \theta {\left(dL\right)}^2}{4\pi r^3}\right)a_{\theta }$

   $\nabla \times dA=\left(\frac{{\mu }_{o}I{\left(dL\right)}^2}{4\pi r^3}\right)\left(2\cos \theta a_r+\sin \theta a_{\theta }\right)$

Now we have $dH=\left(\frac{1}{{\mu }_o}\right)\nabla \times dA$

   $dH=\left(\frac{1}{{\mu }_o}\right)\left(\frac{{\mu }_{o}I{\left(dL\right)}^2}{4\pi r^3}\right)\left(2\cos \theta a_r+\sin \theta a_{\theta }\right)$

   $dH=\left(\frac{I{\left(dL\right)}^2}{4\pi r^3}\right)\left(2\cos \theta a_r+\sin \theta a_{\theta }\right)$

Thus, the relation is proved.