
(a)
To prove:
H is not the function of
Explanation of Solution
Given:
The radius of the hollow cylindrical shell is 'a' which is centered on the z -axis and it carries a surface charge density of
Concept Used:
In this concept, Ampere's circuital law will be used. The law of Ampere states the relationship between the magnetic field and the current one. It says that the closed integration of the magnetic field along the path is equal to the current product contained in the path and the medium. The mathematical expression is given as-
Where,
H = magnetic field
Ienclosed = current within the path
Calculation:
As given a hollow cylinder with a radius of 'a' which is centered on the z-axis.
The surface charge density of this cylinder is
Hollow cylinder along with amperian loop around it shown below-
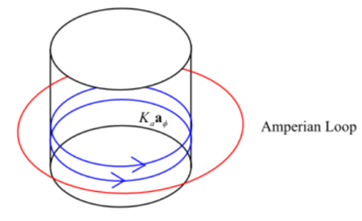
From the above diagram, the value net charge within the loop is zero.
Amperian loop, when the surface charge current element within this loop is given below-
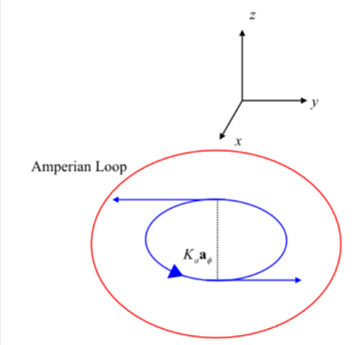
From the above diagram, the direction of the tangent of the current element is aywhich is situated at the diametrically opposite end of the direction of the current element which is -ay.In the same way, every current element's tangent is situated exactly opposite to the direction of the current element.
With this condition, the total charge is canceled out and it will become zero. Therefore,
From, Ampere's circuital law-
So, H =0. This explains that there is no magnetic field outside the cylinder.
Now, create a loop around the hollow cylinder which passes through its axis and also the outside of the hollow cylinder. This is given as-
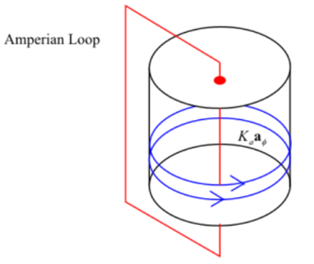
From the above diagram, the direction of surface current is
Therefore, magnetic field intensity is independent of any value of
From the same diagram, assume the length of the cylinder is infinite and the length of the loop is the finite dimension. At this condition, amperian loop cuts the infinite cylinder. Therefore, the net current remainsthe same for the amperian loop of the same dimension in the direction of z.
Therefore magnetic field intensity is independent of any value of z.
Conclusion:
Thus, it is proved that the H is not the function of
(b)
To show:
The value of
Answer to Problem 7.13P
It is proved that
It is proved that
Explanation of Solution
Given:
Radius of hollow cylindrical shell is 'a' which is centered on z- axis and carries uniform surface charge density of
Concept Used:
The concept of Ampere's circuital law and Biot's Savarts will be used. Ampere's circuital law says the closed integration of magnetic field along the path is equal to the product of current within that path and the medium. The mathematical expression is given as-
Where,
H = magnetic field
μ0 = permittivity of the medium
Ienclosed = current within the path
Biot Savart's law is used to calculate the magnetic field generated by the current carrying wire and helps to determine its strength at different points. It helps to relate magnetic field, direction, length, and proximity of electric current. Biot Savart's equation in terms of surface charge density is given as-
Where,
K = surface charge density
Calculation:
As the component
The magnetic field produces the direction of az because the amperian loop encloses the current flowing the direction of az, but there is no current in the direction of az.
Therefore,
The unit vector of the inside loop of the cylinder is given as-
By using Biot Savart's law, we can get the direction of the field which is obtained by K×aR. The component az of aR results in the radial component of magnetic field intensity which is given as-
Where, charge density is
Obtained radial components are opposite to the point at the end of the diameter of the hollow cylinder for constant z.
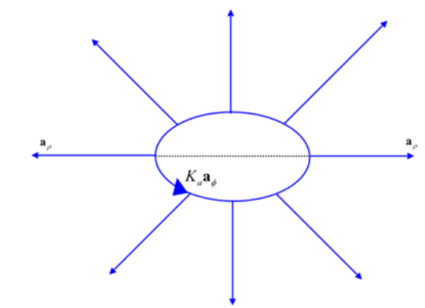
For each current element there is radial component, but these radial elements cancel out by the current element which is located diametrically opposite of radial element at same z. Therefore, the radial component for hollow cylinder shell is
Conclusion:
It is proved that the value of
(c)
To prove:
The value of Hz = 0 for
Answer to Problem 7.13P
By usingAmpere's circuital law,
The current within cylinder is zero and the electric field outside the cylinder is zero. Therefore, the value of Hz = 0 for
Explanation of Solution
Given:
The radius of the hollow cylindrical shell is 'a' which is centered on z -axis and carries uniform surface charge density of
Concept Used:
In this concept of Ampere's circuital law will be used. Ampere's law states the relationship between the current and the magnetic field. It says the closed integration of magnetic field along the path is equal to the product of current within that path and the medium. The mathematical expression is given as-
Where,
H = magnetic field
μ0 = permittivity of the medium
Ienclosed = current within the path
Calculation:
Hollow cylinder along with amperian loop around it is shown below-
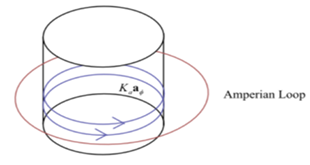
Amperian loop is when the surface charge current element within this loop is given below-

From the above two diagrams, the Amperian loop encompasses the hollow cylindrical shell completely. Therefore, the current within cylinder is zero. So, the electric field outside the cylinder is zero. Thus, the value of the magnetic field is zero for
Conclusion:
By using Ampere's circuital law,
The current within cylinder is zero and the electric filed outside the cylinder is zero. Therefore, the value of
(d)
To prove:
The value of
Answer to Problem 7.13P
By using Biot Savarts equation in terms of surface charge density, the value of magnetic field is
Explanation of Solution
Given:
Radius of hollow cylindrical shell is 'a' which is centered on z -axis and carries uniform surface charge density of
Concept Used:
Biot Savart's law is used to calculate the magnetic field generated by the current carrying wire and helps to determine its strength at different points. It helps to relate magnetic field, direction, length, and proximity of electric current. Biot Savart's equation in terms of surface charge density is given as-
Where,
K = surface charge density
H = magnetic field
Calculation:
Here, a magnetic field is to be calculated at the inside points of the cylinder as it doesn't exist outside the cylinder.
The unit vector of the inside loop of the cylinder is given as-
Biot Savart equation can be written in terms of surface charge density, which is given as-
Where, K is surface charge density, which given as-
Put the value of K and ar in the equation-
As it is already proved that H does not vary with z.
In above equation, put
Limits of θ
On integration
Conclusion:
The value of the magnetic field is
(e)
The value of H everywhere.
Answer to Problem 7.13P
Value of H is
Magnetic field for
Magnetic field for
Magnetic field for
Explanation of Solution
Given:
The radius of the hollow cylindrical shell is 'a' which is centered on z -axis and carries uniform surface charge density of
Concept Used:
In this concept of Ampere's circuital law will be used. Ampere's law states the relationship between the current and the magnetic field. It says the closed integration of magnetic field along the path is equal to the product of current within that path and the medium. The mathematical expression is given as-
Where,
H = magnetic field
μ0 = permitivity of the medium
Ienclosed = current within the path
Calculation:
Plot the amperian loop around the hollow cylinder to get the magnetic field everywhere-
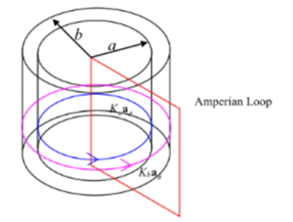
From the above diagram, the magnetic field for
Magnetic field for
Amperian loop for this is
Magnetic field for radius
In this case, no current is within the amperian loop, therefore magnetic field for this case is zero.
Conclusion:
Magnetic field for
Magnetic field for
Magnetic field for
Want to see more full solutions like this?
Chapter 7 Solutions
Engineering Electromagnetics
- Many machines, such as lathes, milling machines, and grinders, are equipped with tracers to reproduce the contours of templates. The figure is a schematic diagram of a hydraulic tracer in which the tool duplicates the shape of the template on the workpiece. a) Explain how the system works. b) Draw a block diagram and identify the system's elements. c) Classify the control system. Oil under pressure Template Style Tool Piece of workarrow_forward2. Refrigerators to maintain the product at a given temperature have a control system. a) Explain how the control system is or how you think it should be (Make a diagram). b) Make the typical block diagram of a control system and identify the components in the refrigerator system. c) Classify the control system.arrow_forward3. Internal combustion engines require a cooling system to function properly, which maintains the engine temperature at an appropriate value. Neither too high nor too low. There are several systems to control this temperature, the two best known are: • The classic one that uses a thermostat that regulates the flow of coolant (water), and where the fan is mechanically coupled to the engine. • In more recent vehicles, in addition to the thermostat, a temperature controller is used that turns an electric fan on and off. Select one of the two systems mentioned above and: a) Explain how it works, using diagrams. b) Make the typical block diagram of a feedback control system, identifying the components of the system. c) Classify the control system.arrow_forward
- A 3-phase, star connected, 10 kVA, 380 V, salient pole alternator with direct and quadrature axis reactances of 15 and 8 0/ph respectively, delivers full-load current at 0.8 power factor lagging. Neglect the armature resistance. Determine the following: (a) The load angle, (b) The direct axis and quadrature axis components of armature current, (c) E.M.F induced voltage of the alternator, (d) The voltage regulation, and (e) The developed power by the alternator?arrow_forwardA 2000 kVA,Y- connected alternator gives an open circuit line voltage of 3.3 kV for a field current of 65 A. For same field current the short circuit current is being equal to full load current. Calculate the full load voltage regulation at both 0.8 lagging p.f. and unity p.f., neglect armature resistance?arrow_forwardDon't use ai to answer I will report you answerarrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





