Chapter 7, Problem 7.30P

(a)

To determine

The lagrangian for the railroad car system and find the equation of motion for the angle $\varphi$.

Answer to Problem 7.30P

The lagrangian for the railroad car system is $L=1/2m\left(a^2{t}^2+2atl\cos \varphi \dot{\varphi }+l^2{\dot{\varphi }}^2\right)+mgl\cos \varphi$  and find the equation of motion for the angle $\varphi$ is $-\sqrt{a^2+g^2}\sin \left(\beta +\varphi \right)$

Explanation of Solution

The figure shows the bob railroad car system.

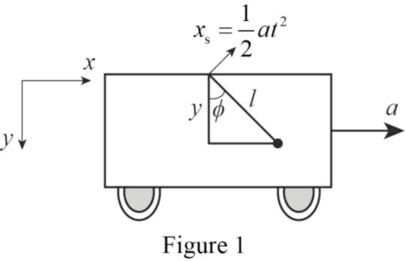
From the figure, the position of the bob,

  $r\left(x,y\right)=\left(l\sin \varphi +\frac{1}{2}a{t}^2,l\cos \varphi \right)$        (I)

Here, $r\left(x,y\right)$ is the position of the coordinates, $l$ is the length of the pendulum, $a$ is the angular acceleration, and $t$ is the time period.

The Cartesian coordinates for the bobs inside an accelerating railroad is,

  $\begin{array}{c}x=l\sin \varphi +\frac{1}{2}a{t}^2\\ y=l\cos \varphi \end{array}$        (II)

We measure y as positive in the downward direction, so differentiate the above two relation with respect to time.

  $\begin{array}{c}\dot{x}=\frac{1}{2}a\left(2t\right)+l\cos \varphi \dot{\varphi }\\ =at+l\cos \varphi \dot{\varphi }\\ \dot{y}=l\left(-\sin \varphi \right)\dot{\varphi }\\ =-l\sin \varphi \dot{\varphi }\end{array}$

The velocity of the bob inside the car is,

  $\begin{array}{c}v=\dot{r}\\ =\left(l\cos \varphi \dot{\varphi }+at,-l\sin \varphi \dot{\varphi }\right)\end{array}$

Then, above relation is written as,

  $\begin{array}{c}{v}^2=v\cdot v\\ ={\left(l\cos \varphi \dot{\varphi }+at\right)}^2+{\left(-l\sin \varphi \dot{\varphi }\right)}^2\\ =l^2{\cos }^2\varphi {\dot{\varphi }}^2+a^2{t}^2+2lat\cos \varphi \dot{\varphi }+l^2{\sin }^2\varphi {\dot{\varphi }}^2\\ =a^2{t}^2+\left({\cos }^2\varphi +{\sin }^2\varphi \right)l^2{\dot{\varphi }}^2+2atl\cos \varphi \dot{\varphi }\\ =a^2{t}^2+l^2{\dot{\varphi }}^2+2atl\cos \varphi \dot{\varphi }\end{array}$ is the

The expression for kinetic energy of the bob is,

  $T=\frac{1}{2}m{v}^2$

Here, $T$ is the kinetic energy, $m$ is the mass of the bob, and $v$ is the velocity.

Conclusion:

Substitute $a^2{t}^2+l^2{\dot{\varphi }}^2+2atl\cos \varphi \dot{\varphi }$ in above relation.

  $T=\frac{1}{2}m{\left(a^2{t}^2+l^2{\dot{\varphi }}^2+2atl\cos \varphi \dot{\varphi }\right)}^2$        (III)

From the figure,

  $\begin{array}{c}\cos \varphi =\frac{y}{l}\\ y=l\cos \varphi \end{array}$

The potential energy of the bob is,

  $\begin{array}{c}U=-mgy\\ =-mgl\cos \varphi \end{array}$                                                                                        …… (IV)                  

The lagrangian equation for the bob railroad system is,

  $L=T-U$

Substitute equation (III) and (IV) in above relation,

  $L=\frac{1}{2}m{\left(a^2{t}^2+l^2{\dot{\varphi }}^2+2atl\cos \varphi \dot{\varphi }\right)}^2+mgl\cos \varphi$

The required quantities for the lagrangian for the coordinate $\varphi$ are,

  $\begin{array}{c}\frac{\partial L}{\partial \varphi }=\frac{\partial }{\partial \varphi }\left[\frac{1}{2}m{\left(a^2{t}^2+l^2{\dot{\varphi }}^2+2atl\cos \varphi \dot{\varphi }\right)}^2+mgl\cos \varphi \right]\\ =\frac{1}{2}m{\left(0+0+2atl\left(-\sin \varphi \right)\dot{\varphi }\right)}^2+mgl\left(-\sin \varphi \right)\\ =-matl\sin \varphi \dot{\varphi }-mgl\sin \varphi \end{array}$

The another quantities are,

  $\begin{array}{c}\frac{\partial L}{\partial \dot{\varphi }}=\frac{\partial }{\partial \dot{\varphi }}\left[\frac{1}{2}m{\left(a^2{t}^2+l^2{\dot{\varphi }}^2+2atl\cos \varphi \dot{\varphi }\right)}^2+mgl\cos \varphi \right]\\ =\frac{1}{2}m{\left(0+\left(2\dot{\varphi }\right)l^2+2atl\cos \varphi \right)}^2+0\\ =matl\cos \varphi +m{l}^2\dot{\varphi }\end{array}$

The Lagrange’s equation for the motion of the bob railroad system for $\varphi$ coordinate is,

  $\begin{array}{c}\frac{\partial L}{\partial \varphi }=\frac{d}{dt}\frac{\partial L}{\partial \dot{\varphi }}\\ -matl\sin \varphi \dot{\varphi }-mgl\sin \varphi =\frac{d}{dt}\left[matl\cos \varphi +m{l}^2\dot{\varphi }\right]\\ -matl\sin \varphi \dot{\varphi }-mgl\sin \varphi =mal\cos \varphi +matl\left(-\sin \varphi \right)\dot{\varphi }+m{l}^2\ddot{\varphi }\\ -at\sin \varphi \dot{\varphi }-g\sin \varphi =a\cos \varphi -at\sin \varphi \dot{\varphi }+l\ddot{\varphi }\end{array}$

The above relation is written as,

  $-g\sin \varphi =a\cos \varphi +l\ddot{\varphi }$

Thus, the Lagrange’s equation for the motion of the bob railroad system is,

  $l\ddot{\varphi }=-g\sin \varphi -a\cos \varphi$

Let us consider $g=A\cos \beta$ and $a=A\sin \beta$ square on both sides of the equations.

  $\begin{array}{c}{a}^2+g^2=A^2{\sin }^2\beta +A^2{\cos }^2\beta \\ a^2+g^2=A^2\left({\sin }^2\beta +{\cos }^2\beta \right)\\ a^2+g^2=A^2\\ A=\sqrt{a^2+g^2}\end{array}$

Thus, the Lagrange’s equation becomes,

  $\begin{array}{c}l\ddot{\varphi }=-A\cos \beta \sin \varphi -A\sin \beta \cos \varphi \\ =-A\left[\cos \beta \sin +\sin \beta \cos \varphi \right]\\ =-A\sin \left(\beta +\varphi \right)\\ =-\sqrt{a^2+g^2}\sin \left(\beta +\varphi \right)\end{array}$

Therefore, the lagrangian for the railroad car system is

$L=1/2m\left(a^2{t}^2+2atl\cos \varphi \dot{\varphi }+l^2{\dot{\varphi }}^2\right)+mgl\cos \varphi$ and find the equation of motion for the angle $\varphi$ is $-\sqrt{a^2+g^2}\sin \left(\beta +\varphi \right)$

(b)

To determine

The equilibrium angle $\varphi$.

Answer to Problem 7.30P

The equilibrium angle $\varphi$ is $\varphi =-{\tan }^{-1}\left(a/g\right)$.

Explanation of Solution

From part (a),

At equilibrium $\ddot{\varphi }=0$, thus the Lagrange’s equation of motion becomes,

  $\begin{array}{c}l\ddot{\varphi }=-g\sin \varphi -a\cos \varphi \\ l\left(0\right)=-g\sin \varphi -a\cos \varphi \\ 0=-g\sin \varphi -a\cos \varphi \end{array}$

Rewrite the equation for $\varphi$.

     $\begin{array}{c}-g\sin \varphi =a\cos \varphi \\ \frac{\sin \varphi }{\cos \varphi }=-\frac{a}{g}\\ \tan \varphi =-\frac{a}{g}\\ \varphi =-{\tan }^{-1}\left(\frac{a}{g}\right)\end{array}$

Conclusion:

At equilibrium $\ddot{\varphi }=0$, thus the Lagrange’s equation of motion becomes,

  $\begin{array}{c}l\ddot{\varphi }=-\sqrt{a^2+g^2}\sin \left(\beta +\varphi \right)\\ l\left(0\right)=-\sqrt{a^2+g^2}\sin \left(\beta +\varphi \right)\\ 0=\sin \left(\beta +\varphi \right)\end{array}$

Rewrite the equation for $\varphi$.

  $\begin{array}{c}\beta +\varphi ={\sin }^{-1}\left(0\right)\\ \beta +\varphi =0\\ \varphi =-\beta \end{array}$

The expression for Lagrange’s equation,

  $\begin{array}{c}l\ddot{\varphi }=-\sqrt{a^2+g^2}\sin \left(\beta +\varphi \right)\\ \ddot{\varphi }=-\frac{\sqrt{a^2+g^2}}{l}\sin \left(\beta +\varphi \right)\end{array}$

If bob is slightly displaced from its equilibrium position, Lagrange’s equation becomes,

  $\ddot{\varphi }=-\frac{\sqrt{a^2+g^2}}{l}\sin \left(\delta \varphi \right)$

Therefore, the equilibrium angle $\varphi$ is $\varphi =-{\tan }^{-1}\left(a/g\right)$.