
The lagrangian for a projectile.
Answer to Problem 7.1P
The three lagrangian for a projectile are,
Explanation of Solution
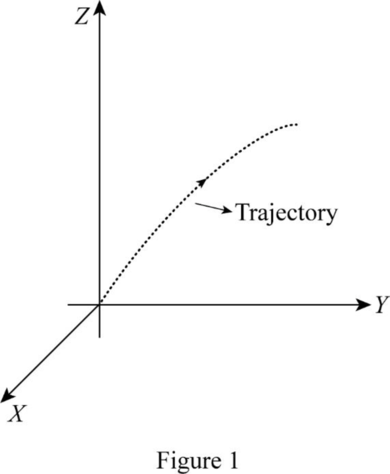
The lagrangian of the projectile system is,
Here,
For this projectile the kinetic energy is,
Here,
The velocity of the projectile in terms of Cartesian coordinates is,
Substitute the expression (III) in (II)
The potential energy of the projectile is,
Here,
Substitute the expression (IV) and (V) in expression (I)
The lagrangian equation for the projectile along
Calculate
Calculate
Conclusion:
Substitute
Therefore, the first lagrangian equation for the projectile is
The lagrangian equation for the projectile along
Calculate
Calculate
Substitute
Therefore, the second lagrangian equation for the projectile is
The lagrangian equation for the projectile along
Calculate
Calculate
Substitute
Therefore, the third lagrangian equation for the projectile is
Want to see more full solutions like this?
Chapter 7 Solutions
Classical Mechanics
- What All equations of Ountum physics?arrow_forwardPlease rewrite the rules of Quantum mechanics?arrow_forwardSuppose there are two transformers between your house and the high-voltage transmission line that distributes the power. In addition, assume your house is the only one using electric power. At a substation the primary of a step-down transformer (turns ratio = 1:23) receives the voltage from the high-voltage transmission line. Because of your usage, a current of 51.1 mA exists in the primary of the transformer. The secondary is connected to the primary of another step-down transformer (turns ratio = 1:36) somewhere near your house, perhaps up on a telephone pole. The secondary of this transformer delivers a 240-V emf to your house. How much power is your house using? Remember that the current and voltage given in this problem are rms values.arrow_forward
- The human eye is most sensitive to light having a frequency of about 5.5 × 1014 Hz, which is in the yellow-green region of the electromagnetic spectrum. How many wavelengths of this light can fit across a distance of 2.2 cm?arrow_forwardA one-dimensional harmonic oscillator of mass m and angular frequency w is in a heat bath of temperature T. What is the root mean square of the displacement of the oscillator? (In the expressions below k is the Boltzmann constant.) Select one: ○ (KT/mw²)1/2 ○ (KT/mw²)-1/2 ○ kT/w O (KT/mw²) 1/2In(2)arrow_forwardTwo polarizers are placed on top of each other so that their transmission axes coincide. If unpolarized light falls on the system, the transmitted intensity is lo. What is the transmitted intensity if one of the polarizers is rotated by 30 degrees? Select one: ○ 10/4 ○ 0.866 lo ○ 310/4 01/2 10/2arrow_forward
- Before attempting this problem, review Conceptual Example 7. The intensity of the light that reaches the photocell in the drawing is 160 W/m², when 0 = 18°. What would be the intensity reaching the photocell if the analyzer were removed from the setup, everything else remaining the same? Light Photocell Polarizer Insert Analyzerarrow_forwardThe lifetime of a muon in its rest frame is 2.2 microseconds. What is the lifetime of the muon measured in the laboratory frame, where the muon's kinetic energy is 53 MeV? It is known that the rest energy of the muon is 106 MeV. Select one: O 4.4 microseconds O 6.6 microseconds O 3.3 microseconds O 1.1 microsecondsarrow_forwardThe Lagrangian of a particle performing harmonic oscil- lations is written in the form L = ax² - Bx² - yx, where a, and are constants. What is the angular frequency of oscillations? A) √2/a B) √(+2a)/B C) √√Ba D) B/αarrow_forward
- The mean temperature of the Earth is T=287 K. What would the new mean temperature T' be if the mean distance between the Earth and the Sun was increased by 2%? Select one: ○ 293 K O 281 K ○ 273 K 284 Karrow_forwardTwo concentric current-carrying wire loops of radius 3 cm and 9 cm lie in the same plane. The currents in the loops flow in the same direction and are equal in magnitude. The magnetic field at the common center of the loops is 50 mT. What would be the value of magnetic field at the center if the direction of the two currents was opposite to each other (but their value is kept constant)? Select one: ○ 20 mT ○ 10 mT O 15 mT ○ 25 mTarrow_forwardAn ideal coil of inductivity 50 mH is connected in series with a resistor of 50 ohm. This system is connected to a 4.5 V battery for a long time. What is the current in the circuit? Select one: O 45 mA ○ 90 mA 00 mA O 150 mAarrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





