Chapter 7, Problem 7.23QP

Light Energy, and the Hydrogen Atom

1. a Which has the greater wavelength, blue light or red light?
2. b How do the frequencies of blue light and red light compare?
3. c How does the energy of blue light compare with that of red light?
4. d Does blue light have a greater speed than red light?
   1. e How does the energy of three photons from a blue light source compare with the energy of one photon of blue light from the same source? How does the energy of two photons corresponding to a wavelength of 451 nm (blue light) compare with the energy of three photons corresponding to a wavelength of 704 nm (red light)?
   2. f A hydrogen atom with an electron in its ground state interacts with a photon of light with a wavelength of 1.22 × 10⁻⁶ m. Could the electron make a transition from the ground state to a higher energy level? If it does make a transition, indicate which one. If no transition can occur, explain.
   3. g If you have one mole of hydrogen atoms with their electrons in the n = 1 level, what is the minimum number of photons you would need to interact with these atoms in order to have all of their electrons promoted to the n = 3 level? What wavelength of light would you need to perform this experiment?

Interpretation Introduction

Interpretation:

The light with higher wavelength has to be identified from the given lights.

Concept introduction:

Relation between frequency and wavelength is,

$\text{C}\text{=}\text{λν}$

C is the speed of light.

$\text{ν}$ is the frequency.

$\text{λ}$ is wavelength.

$\text{E}\text{=}\text{hν}$

h is Planck’s constant ( $\text{6}\text{.63}\text{×}{\text{10}}^{\text{-34}}\text{J}\text{.s}$ ) which relates energy and frequency.

$\text{ν}$ is the frequency

E is energy of light particle.

Wavelength and frequency are inversely proportional to each other.

The distance between any two similar points of a wave is called wavelength

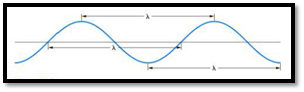
Figure 1

Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.

Answer to Problem 7.23QP

Red light has larger wavelength than blue light.

Explanation of Solution

To identify: The light with higher wavelength.

Wavelength and frequency are inversely proportional to each other.  Frequency of blue light is higher than red light.  Thus, red light has larger wavelength than blue light.

Conclusion

By using the relation between wavelength and frequency, the light with higher wavelength was identified.

Interpretation Introduction

Interpretation:

The light with higher frequency has to be identified from the given lights.

Concept introduction:

Relation between frequency and wavelength is,

$\text{C}\text{=}\text{λν}$

C is the speed of light.

$\text{ν}$ is the frequency.

$\text{λ}$ is wavelength.

$\text{E}\text{=}\text{hν}$

h is Planck’s constant ( $\text{6}\text{.63}\text{×}{\text{10}}^{\text{-34}}\text{J}\text{.s}$ ) which relates energy and frequency.

$\text{ν}$ is the frequency

E is energy of light particle.

Wavelength and frequency are inversely proportional to each other.

The distance between any two similar points of a wave is called wavelength

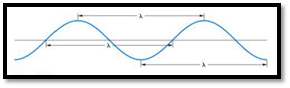
Figure 1

Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.

Answer to Problem 7.23QP

Blue light has larger frequency than red light.

Explanation of Solution

To identify: The light with higher frequency.

Wavelength and frequency are inversely proportional to each other.  Wavelength of blue light is less than red light.  Thus, blue light has larger frequency than red light.

Conclusion

By using the relation between wavelength and frequency, the light with higher frequency was identified.

Interpretation Introduction

Interpretation:

The energies of blue light and red light has to be related.

Concept introduction:

Relation between frequency and wavelength is,

$\text{C}\text{=}\text{λν}$

C is the speed of light.

$\text{ν}$ is the frequency.

$\text{λ}$ is wavelength.

$\text{E}\text{=}\text{hν}$

h is Planck’s constant ( $\text{6}\text{.63}\text{×}{\text{10}}^{\text{-34}}\text{J}\text{.s}$ ) which relates energy and frequency.

$\text{ν}$ is the frequency

E is energy of light particle.

Wavelength and frequency are inversely proportional to each other.

The distance between any two similar points of a wave is called wavelength

Figure 1

Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.

Answer to Problem 7.23QP

Blue light has higher energy than red light.

Explanation of Solution

To compare: The energy of blue light and red light.

Energy and frequency are directly proportional to each other.  Frequency of blue light is higher than red light.  Thus, blue light has higher energy than red light.

Conclusion

By using the relation between wavelength and frequency, the energy of blue light and red light was related.

Interpretation Introduction

Interpretation:

The speed of blue light and red light has to be compared.

Concept introduction:

Relation between frequency and wavelength is,

$\text{C}\text{=}\text{λν}$

C is the speed of light.

$\text{ν}$ is the frequency.

$\text{λ}$ is wavelength.

$\text{E}\text{=}\text{hν}$

h is Planck’s constant ( $\text{6}\text{.63}\text{×}{\text{10}}^{\text{-34}}\text{J}\text{.s}$ ) which relates energy and frequency.

$\text{ν}$ is the frequency

E is energy of light particle.

Wavelength and frequency are inversely proportional to each other.

The distance between any two similar points of a wave is called wavelength

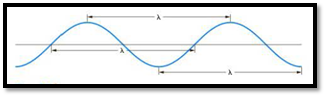
Figure 1

Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.

Answer to Problem 7.23QP

Blue light has higher energy than red light.

Explanation of Solution

To compare: The speed of blue light and red light.

Energy and frequency are directly proportional to each other.  Frequency of blue light is higher than red light.  Thus, blue light has higher energy than red light.

Conclusion

By using the relation between wavelength and frequency, the energy of blue light and red light was related.

Interpretation Introduction

Interpretation:

The energy of one photon and energy of three photons of blue light has to be compared.

Concept introduction:

Relation between frequency and wavelength is,

$\text{C}\text{=}\text{λν}$

C is the speed of light.

$\text{ν}$ is the frequency.

$\text{λ}$ is wavelength.

$\text{E}\text{=}\text{hν}$

h is Planck’s constant ( $\text{6}\text{.63}\text{×}{\text{10}}^{\text{-34}}\text{J}\text{.s}$ ) which relates energy and frequency.

$\text{ν}$ is the frequency

E is energy of light particle.

Wavelength and frequency are inversely proportional to each other.

The distance between any two similar points of a wave is called wavelength

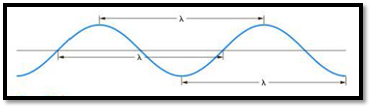
Figure 1

Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.

Answer to Problem 7.23QP

Blue light ( $\text{451 nm}$) has energy of two photons which is $1.04$ times greater than red light ( $\text{704 nm}$) with energy of three photons.

Explanation of Solution

To compare: The energy of one photon and energy of three photons of blue light.

Blue light with energy of three photons is thrice the energy of one photon. In order to relate the energy of two photon (blue light) with energy of three photon (red light), the energy is given as $\text{E}\text{=}\frac{\text{nhc}}{\text{λ}}$

$\begin{array}{l}\frac{{\text{E}}_{\text{blue}}}{{\text{E}}_{\text{red}}}\text{=}\frac{\frac{{\text{n}}_{\text{blue}}\text{hc}}{\text{λ}}}{\frac{{\text{n}}_{\text{red}}\text{hc}}{\text{λ}}}\\ \text{=}\frac{{\text{n}}_{\text{blue}}{\text{λ}}_{\text{red}}}{{\text{n}}_{\text{red}}{\text{λ}}_{\text{blue}}}\\ \\ \text{=}\frac{\text{(2)(704 nm)}}{\text{(3)(451 nm)}}\text{=}\text{1}\text{.04}\end{array}$

Blue light ( $\text{451 nm}$) has energy of two photons which is $1.04$ times greater than red light ( $\text{704 nm}$) with energy of three photons.

Conclusion

By using the relation between wavelength and frequency, the energy of two photon of blue light and energy of three photons of red light was related.

Interpretation Introduction

Interpretation:

The possibility of transition of an electron of hydrogen atom from ground state to higher energy state has to be determined.

Concept introduction:

Relation between frequency and wavelength is,

$\text{C}\text{=}\text{λν}$

C is the speed of light.

$\text{ν}$ is the frequency.

$\text{λ}$ is wavelength.

$\text{E}\text{=}\text{hν}$

h is Planck’s constant ( $\text{6}\text{.63}\text{×}{\text{10}}^{\text{-34}}\text{J}\text{.s}$ ) which relates energy and frequency.

$\text{ν}$ is the frequency

E is energy of light particle.

Wavelength and frequency are inversely proportional to each other.

The distance between any two similar points of a wave is called wavelength

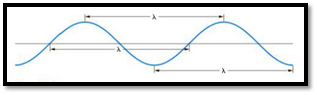
Figure 1

Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.

Bohr developed a rule for quantization of energy that could be applicable to the electron of an atom in motion.  By using this he derived a formula for energy levels of electron in H-atom.

$\begin{array}{l}\text{E}\text{=}\frac{{\text{-R}}_{\text{H}}}{{\text{n}}^{\text{2}}}\text{n}\text{=}\text{1,2,3,}\mathrm{......}\text{(For}\text{hydrogen}\text{atom)}\\ \\ {\text{R}}_{\text{H}}\text{is}\text{Rydberg}\text{constant}\text{(2}\text{.179}\text{×}{\text{10}}^{\text{-18}}\text{J)}\text{.}\\ \text{Eis}\text{energy}\text{level}\text{.}\\ \text{n}\text{is}\text{principal}\text{quantum}\text{number}\text{.}\end{array}$

Answer to Problem 7.23QP

The obtained energy for transition is greater than the energy of light.  Therefore, no transition occurs.

Explanation of Solution

To determine: The possibility of transition of an electron of hydrogen atom from ground state to higher energy state.

By using the below formula and calculate frequency and energy of light

$\begin{array}{l}\text{C}\text{=}\text{λν}\\ \\ \text{ν}\text{=}\frac{\text{C}}{\text{λ}}\text{=}\frac{\text{2}\text{.998}\text{×}{\text{10}}^{\text{8}}\text{m/s}}{1.22\text{×}{\text{10}}^{\text{-6}}\text{m}}\text{=}\text{2}\text{.459}\text{×}{\text{10}}^{\text{14}}\text{/s}\end{array}$

$\begin{array}{l}\text{E}\text{=}\text{hν}\\ \text{=}\text{(6}\text{.63 ×}{\text{10}}^{\text{-34}}\text{J}\text{.s)}\text{×}(2.459\text{×}{\text{10}}^{\text{14}}\text{/s)}\\ \text{=}\text{1}\text{.630}\text{×}{\text{10}}^{\text{-19}}\text{J}\end{array}$

The minimum energy required for the transition of $\text{n = 1 to n = 2}$  is calculated as follows,

$\begin{array}{l}\text{E}\text{=}{\text{-R}}_{\text{H}}\left(\frac{\text{1}}{{\text{n}}_{\text{f}}{}^{\text{2}}}\text{-}\frac{\text{1}}{{\text{n}}_{\text{i}}{}^{\text{2}}}\right)\\ \\ \text{=}\text{(2}\text{.179}\text{×}{\text{10}}^{\text{-18}}\text{J)}\left(\frac{\text{1}}{{\text{2}}^{\text{2}}}\text{-}\frac{\text{1}}{{\text{1}}^{\text{2}}}\right)\\ \\ \text{=}\text{1}\text{.6345}\text{×}{\text{10}}^{\text{-18}}\text{J}\end{array}$

The obtained energy for transition is greater than the energy of light.  Therefore, no transition occurs.

Conclusion

The possibility of transition of an electron of hydrogen atom from ground state to higher energy state was determined.

Interpretation Introduction

Interpretation:

The energy required for transition of an electron of hydrogen atom from $\text{n}\text{=}\text{1}\text{to}\text{n}\text{=}\text{3}$ level has to be determined.  Also the wavelength of the light has to be calculated.

Concept introduction:

Relation between frequency and wavelength is,

$\text{C}\text{=}\text{λν}$

C is the speed of light.

$\text{ν}$ is the frequency.

$\text{λ}$ is wavelength.

$\text{E}\text{=}\text{hν}$

h is Planck’s constant ( $\text{6}\text{.63}\text{×}{\text{10}}^{\text{-34}}\text{J}\text{.s}$ ) which relates energy and frequency.

$\text{ν}$ is the frequency

E is energy of light particle.

Wavelength and frequency are inversely proportional to each other.

The distance between any two similar points of a wave is called wavelength

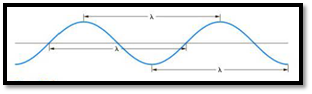
Figure 1

Frequency is defined as number of wavelengths of a wave that can pass through a point in one second.

Bohr developed a rule for quantization of energy that could be applicable to the electron of an atom in motion.  By using this he derived a formula for energy levels of electron in H-atom.

$\begin{array}{l}\text{E}\text{=}\frac{{\text{-R}}_{\text{H}}}{{\text{n}}^{\text{2}}}\text{n}\text{=}\text{1,2,3,}\mathrm{......}\text{(For}\text{hydrogen}\text{atom)}\\ \\ {\text{R}}_{\text{H}}\text{is}\text{Rydberg}\text{constant}\text{(2}\text{.179}\text{×}{\text{10}}^{\text{-18}}\text{J)}\text{.}\\ \text{Eis}\text{energy}\text{level}\text{.}\\ \text{n}\text{is}\text{principal}\text{quantum}\text{number}\text{.}\end{array}$

Answer to Problem 7.23QP

The minimum energy required for the transition of $\text{n = 1 to n = 3}$  is $\text{1}\text{.9368}\text{×}{\text{10}}^{\text{-18}}\text{J}$.

The wavelength of the light is $\text{1}\text{.03}\text{×}{\text{10}}^{\text{-7}}\text{m}\text{(103}\text{nm)}$.

Explanation of Solution

To determine: The energy required for transition of an electron of hydrogen atom from $\text{n}\text{=}\text{1}\text{to}\text{n}\text{=}\text{3}$ level.

The minimum energy required for the transition of $\text{n = 1 to n = 3}$  is calculated as follows,

$\begin{array}{l}\text{E}\text{=}{\text{-R}}_{\text{H}}\left(\frac{\text{1}}{{\text{n}}_{\text{f}}{}^{\text{2}}}\text{-}\frac{\text{1}}{{\text{n}}_{\text{i}}{}^{\text{2}}}\right)\\ \\ \text{=}\text{(2}\text{.179}\text{×}{\text{10}}^{\text{-18}}\text{J)}\left(\frac{\text{1}}{3^{\text{2}}}\text{-}\frac{\text{1}}{{\text{1}}^{\text{2}}}\right)\\ \\ \text{=}\text{1}\text{.9368}\text{×}{\text{10}}^{\text{-18}}\text{J}\end{array}$

$\begin{array}{l}\text{E}\text{=}\text{hν}\\ \\ \text{ν}\text{=}\frac{\text{E}}{\text{h}}\text{=}\frac{\text{1}\text{.9368}\text{×}{\text{10}}^{\text{-18}}\text{J}}{\text{6}\text{.63 ×}{\text{10}}^{\text{-34}}\text{J}\text{.s}}\text{=}\text{2}\text{.921}\text{×}{\text{10}}^{\text{15}}\text{/s}\end{array}$

$\begin{array}{l}\text{C}\text{=}\text{λν}\\ \\ \text{λ}\text{=}\frac{\text{C}}{\text{ν}}\text{=}\frac{\text{2}\text{.998}\text{×}{\text{10}}^{\text{8}}\text{m/s}}{\text{2}\text{.921}\text{×}{\text{10}}^{\text{15}}\text{/s}}\text{=}\text{1}\text{.03}\text{×}{\text{10}}^{\text{-7}}\text{m}\text{(103}\text{nm)}\end{array}$

Conclusion

The energy required for transition of an electron of hydrogen atom from $\text{n}\text{=}\text{1}\text{to}\text{n}\text{=}\text{3}$ level was determined.  Also the wavelength of the light was calculated.