
- (a) Revisit Example 7-1. What is the error in assuming the concentration of species B is constant and what limits can you put on the calculated value of k? (I.e., k = 0.24 ±?)
- (b) Revisit Example 7-3. Explain why the regression was carried out twice to find k′ and k.
- (c) Revisit Example 7-4. Regress the data to lit the rate law
What is the difference in the correlation and sums of squares compared with those given in Example 7-4? Why was it necessary to regress the data twice, once to obtain Table E7-4.3 and once to obtain Table E7-4.4?
(a)
Interpretation:
The error in assuming the concentration of species B is constant and the limits that can be put over the calculated value of
Concept introduction:
The integral method is the quickest method to use to determine the rate law if the order turns out to zero, first, or second order. In the integral method, we guess the reaction order, α, in the combined batch reactor mole balance and rate law equation.
Integrate the differential equation to obtain the concentration as a function of time. If the order we assume is correct, the appropriate plot of the concentration-time data should be linear. The integral method is used most often when the reaction order is known and it is desired to evaluate the specific reaction rate constant at different temperatures to determine the activation energy.
Answer to Problem 7.1P
The error in assuming the concentration of species B is constant and the limits that can be put over the calculated value of
Explanation of Solution
The given liquid phase reaction which takes place in a batch reactor is as follows.
The initial concentration of Trityl (A) in the feed is
The initial concentration of methanol (B) in the feed is
The temperature of the batch reactor is
The data for time and various concentration of A is given in the table below.
The rate law for the above mentioned reaction is given below.
Where,
The value of
Where,
Substitute
The value of
Substitute
So, the differential rate equation for the equation is given below.
The integration of the above equation with appropriate limits is given below and Substitute
If
Thus, the value of conversion,
| 0 | |||||||
Thus, the graph that can be plotted between
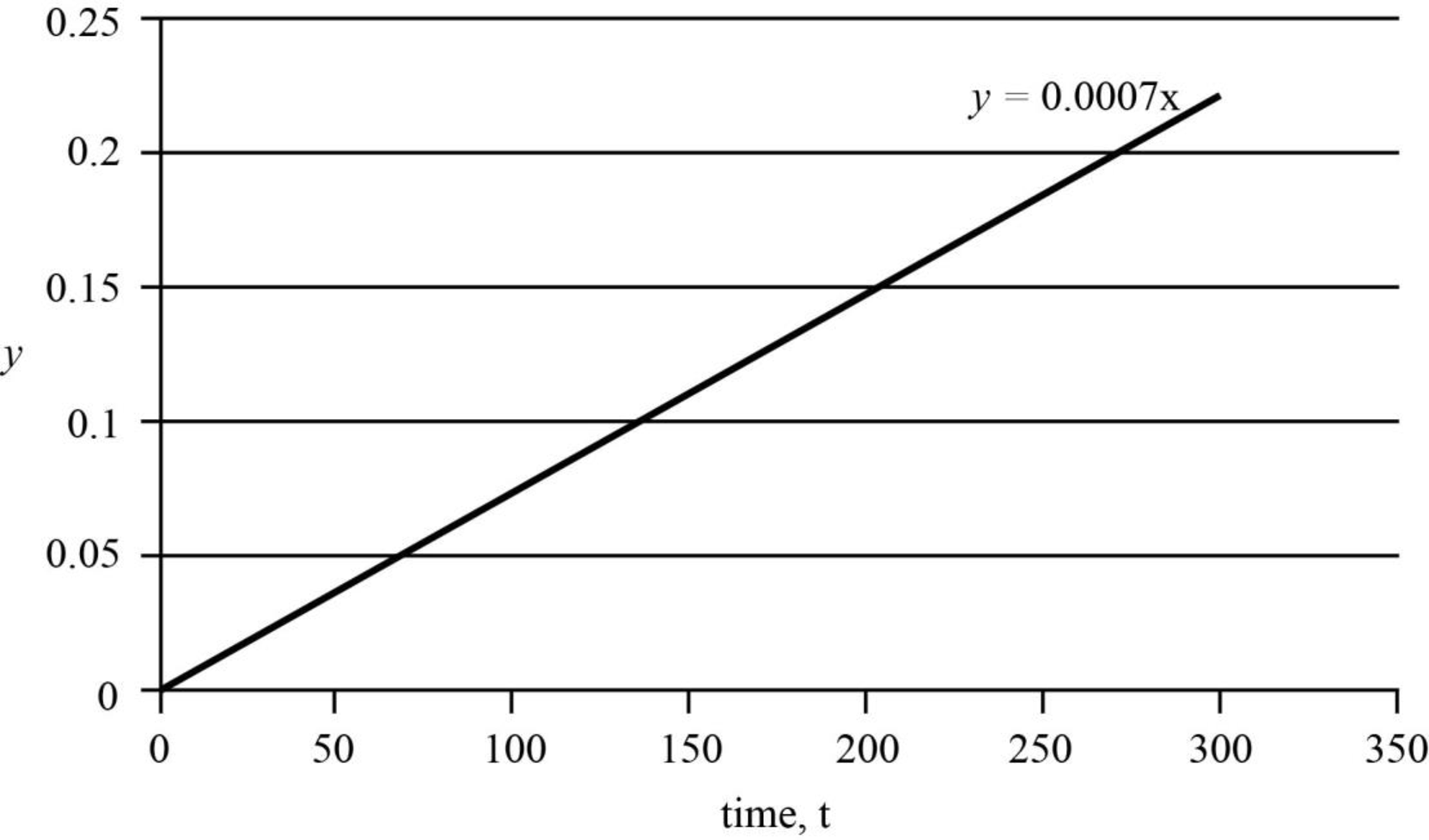
Figure 1
The intercept,
The actual value of
(b)
Interpretation:
The reason as to why regression is carried out twice to find
Concept Introduction:
In nonlinear regression analysis, we search for those parameter values that minimize the sum of the squares of the differences between the measured values and the calculated values for all the data points.
The initial estimates of the parameter values (e.g., reaction order, specific rate constant) in order to calculate the concentration for each data point,
Explanation of Solution
After the first regression, the equation order is predicted
Thus, the value of rate constant can only be calculated at
(c)
Interpretation:
The difference between correlation and sums of square compared with values in the given example is to be stated. The reason as to why regression is carried out twice is to be stated.
Concept Introduction:
In nonlinear regression analysis, we search for those parameter values that minimize the sum of the squares of the differences between the measured values and the calculated values for all the data points.
The initial estimates of the parameter values (e.g., reaction order, specific rate constant) in order to calculate the concentration for each data point,
Explanation of Solution
The given rate law is as follows.
During the first regression, the equation order is predicted as an integer and the corresponding rate constant is also integer. So, the regression is proceeded at the order of
Want to see more full solutions like this?
Chapter 7 Solutions
ELEMENTS OF CHEM. REACTION ENGR
Additional Engineering Textbook Solutions
Thermodynamics: An Engineering Approach
Starting Out With Visual Basic (8th Edition)
Starting Out with C++ from Control Structures to Objects (9th Edition)
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
Computer Science: An Overview (13th Edition) (What's New in Computer Science)
Starting Out with Python (4th Edition)
- Use the binary diagram, 45 line above and material balance to solve the One thousand kg/h of a (50-50 wt%) acetone-in-water solution is to be extracted at 25C in a continuous, countercurrent system with pure 1,1,2-trichloroethane to obtain a raffinate containing 10 wt% acetone. Using the following equilibrium data, determine with an equilateral-triangle diagram: a the minimum flow rate of solvent; b. the number of stages required for a solvent rate equal to 1.5 times minimum, and composition of each streamleaving each stage. Repeat the calculation of (a) and (b) if the solvent used has purity 93wt% (4wr% acetone, 3wt% water impurities) acetone 0.6 water 0.13 1,1,2-trichloroethane 0.27 Raffinate. Weight Fraction Acetone Extract. Weight Fraction Acetone 0.5 0.04 0.46 0.44 0.56 0.4 0.03 0.57 0.29 0.40 0.3 0.02 0.681 0.12 0.18 0.2 0.015 0.785 0.0 0.0 0.1 0.01 0.89 0.55 0.35 0.1 0.5 0.43 0.07 0.4 0.57 0.03 0.3 0.68 0.02 0.2 0.79 0.01 0.1 0.895 0.005arrow_forwardMaterial Sciencearrow_forwardMaterial Sciencearrow_forward
- Material Sciencearrow_forwardTernary Phase Diagram+ Material balance One thousand kg/h of a (50-50 wt%) acetone-in-water solution is to be extracted at 25C in a continuous, countercurrent system with pure 1,1,2-trichloroethane to obtain a raffinate containing 10 wt% acetone. Using the following equilibrium data, determine with an equilateral-triangle diagram: a- the minimum flow rate of solvent; b- the number of stages required for a solvent rate equal to 1.5 times minimum, and composition of each streamleaving each stage. c. Repeat the calculation of (a) and (b) if the solvent used has purity 93wt% (4wr% acetone, 3wt% water impurities) acetone water 1,1,2-trichloroethane Raffinate. Weight Extract. Weight 0.6 0.13 0.27 Fraction Acetone Fraction Acetone 0.5 0.04 0.46 0.44 0.56 0.4 0.03 0.57 0.29 0.40 0.3 0.02 0.68 0.12 0.18 0.2 0.015 0.785 0.0 0.0 0.1 0.01 0.89 0.55 0.35 0.1 0.5 0.43 0.07 0.4 0.57 0.03 0.3 0.68 0.02 0.2 0.79 0.01 0.1 0.895 0.005arrow_forwardI need a detailed drawing with explanation so A 4 しか شكا Write a complete C++ program that includes a function to check whether a given sequence of parentheses is balanced using stack or Linked stack 7:30 م PU + 9625 =-2c125 750 x2.01 58³arrow_forward
- Ternary Phase Diagram+ Material balance Feed mixture weighing 200 kg of unknown composition containing water, acetic acid, isopropyl ether is contacted in a single stage with 280kg mixture containing 40wt% acetic acid. 10wt% water and 50wt% isopropyl ether. The resulting raffinate layer weight 320 kg and containing 29.5 wt% acetic acid, 66.5 wt% water and 4wt% isopropyl ether. Determine the composition of the original feed mixture and the extract layer Water layer Isopropyl ether layer acetic acid 0 water 98.8 Isopropyl ether 1.2 acetic acid 0 water Isopropyl ether 0.6 99.4 0.69 98.1 1.2 0.18 0.5 99.3 1.41 97.1 1.5 0.37 0.7 98.9 2.89 95.5 1.6 0.79 0.8 98.4 6.42 91.7 1.9 1.93 1 97.1 13.3 84.4 2.3 4.82 1.9 93.3 25.5 71.1 3.4 11.4 3.9 84.7 36.7 58.9 4.4 21.6 6.9 71.5 44.3 5.1 10.6 31.1 10.8 58.5 46.4 37.1 16.5 36.2 15.1 48.7arrow_forwardGraphically+Material balance 2500 kg/hr of (20-80) nicotine water solution is to be extracted with benzene containing 0.5% nicotine in the 1st and 2nd stages while the 3rd stage is free of nicotine. Cross-current operation is used with different amounts of solvent for each stages 2000kg/hr in the 1st stage, 2300 kg/hr in the 2nd stage, 2600 kg/hr in the 3rd, determine:- a- The final raffinate concentration and % extraction. b- b-The minimum amount of solvent required for counter-current operation if the minimum concentration will be reduced to 5% in the outlet raffinate. Equilibrium data Wt % Nicotine in water 0 4 16 25 Wt % Nicotine in benzene 0 4 21 30arrow_forwardgraphically +material balance 1000 Kg/hr on an acetone water mixture containing 10% of acetone is to be extracted with trichloroethane. The recovered solvent to be used is free of acetone. If 95% recovery of acetone is desired, the equilibrium relationship is given by kg acetone/kg trichloroethane 1.65 kg acetone/kg water. Estimate the number of stages required if 1.5 times the minimum solvent is used when: - a- b- Cross-current is to be extracted. b- Counter-current is to be extracted.arrow_forward
- use Graphically 1000 Kg/hr on an acetone water mixture containing 10% of acetone is to be extracted with trichloroethane. The recovered solvent to be used is free of acetone. If 95% recovery of acetone is desired, the equilibrium relationship is given by kg acetone/kg trichloroethane 1.65 kg acetone/kg water. Estimate the number of stages required if 1.5 times the minimum solvent is used when: - Cross-current is to be extracted. a- b- b- Counter-current is to be extracted.arrow_forwardA solution of 5% acetaldehyde in toluene is to be extracted with water in five stage co-current operation. If 25kg/100kg feed is used, what is the mass of acetaldehyde extracted and the final concentration? The Equilibrium relation is given by: kg acetaldehyde /kg water = 2.2 kg acetaldehyde / kg toluene.arrow_forwardFeed mixture weighing 200 kg of unknown composition containing water, acetic acid, isopropyl ether is contacted in a single stage with 280kg mixture containing 40wt% acetic acid. 10wt% water and 50wt% isopropyl ether. The resulting raffinate layer weight 320 kg and containing 29.5wt% acetic acid, 66.5 wt% water and 4wt% isopropyl ether. Determine the composition of the original feed mixture and the extract layer Water layer Isopropyl ether layer acetic acid water Isopropyl ether acetic acid water Isopropyl ether 0 98.8 1.2 0 0.6 99.4 0.69 98.1 1.2 0.18 0.5 99.3 1.41 97.1 1.5 0.37 0.7 98.9 2.89 95.5 1.6 0.79 0.8 98.4 6.42 91.7 1.9 1.93 1 97.1 13.3 84.4 2.3 4.82 1.9 93.3 25.5 71.1 3.4 11.4 3.9 84.7 36.7 58.9 4.4 21.6 6.9 71.5 44.3 5.1 10.6 31.1 10.8 58.5 46.4 37.1 16.5 36.2 15.1 48.7arrow_forward
 Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
 Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The





